
Weekend Mathematics/コロキウム室/NO.131
| NO.1116 | 2002.1.1. | Junko | 謹賀新年 |
2002年のお正月、あけましておめでとうございます。
本年も引き続きどうぞよろしくお願いいたします。
私自身、昨年は「数学」よりも「情報」に関わることの方が多い1年でした。
高等学校では、2003年からの新カリキュラムということで新教科「情報」が始まります。
新しい教科の立ち上げというめったにないタイミングに居合わせたというのは
幸運なことだと思っています。新しいことにチャレンジするというのは素晴らしいことです。
しかしながら「情報」に関わる中で逆に、やはり私のbaseは「数学」だと感じることも多いです。
このコロキウム室を通じて、皆さんと「数学」のおもしろさを共有できればと思っています。

| NO.1117 | 2002.1.1. | 水の流れ | ある不等式の証明(4) |
ここに、書かれている不等式はコーシー・シュワルツの不等式と言われているものです。
高校の教科書にも出てきますから、参考にして証明します。
問題:a,bは定数で,a<bとする。
tを任意の実数とするとき,定積分
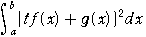 は、tの関数であり,その値が,常に正または
0であることを用いて,次の不等式を証明せよ.
は、tの関数であり,その値が,常に正または
0であることを用いて,次の不等式を証明せよ.
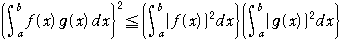
証明
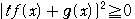 かつa<bであるから
かつa<bであるから
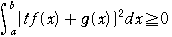
ゆえに
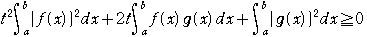 ……①
……①
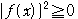 であるから
であるから
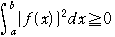 で,
で,
この不等式の等号は,常にf(x)=0であるときに限って成り立つ.
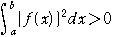 の場合,
①が任意の実数tに対して成り立つための必要十分条件は,
の場合,
①が任意の実数tに対して成り立つための必要十分条件は,
左辺=0とおいたtの2次方程式の判別式Dについて,
D≦0となることである.
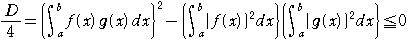
すなわち
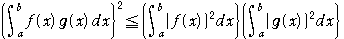 ……②
……②
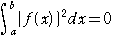 の場合,常に
f(x)=0であるから
の場合,常に
f(x)=0であるから
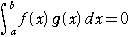
したがって,この場合も②が成り立つ.

| NO.1118 | 2002.1.1. | DDT | 関数の内積 |
[関数の内積を納得したい!]
1.はじめに
突然ですが、関数fとgの内積などと初めて聞いたとき、こんなものを想像してました。
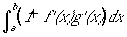 (1)
(1)
式(1)の意味は、関数y=f(x)とy=g(x)のxにおける接線ベクトルが
(1,f'(x))と(1,g'(x))なので、f(x)とg(x)を接線ベクトルの集まりと考えて、
各点で(1,f'(x))と(1,g'(x))内積をとり、それを∫で合計して関数全体の内積とする、
くらいの意味です。要は、高校以来の矢線ベクトルに関して、
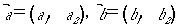
の内積は、
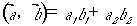
である、というイメージから一歩も外に出られなかったわけです。
以下の文章は、ベクトルとは必ず矢線ベクトルのことであり、
しかも矢線ベクトルと位置ベクトルの区別もつかず、
内積とは位置ベクトル間のab・cosθのことだと思い込んでいたずぶの素人が、
馴染みのない数学的概念にどうやって慣れていったかのサンプルとして読んで頂ければ幸いです。
2.なんで関数空間なんだ!
そもそもなんで関数空間なんでしょう?。
今では関数空間の意味もわかってるつもりですが、初めて関数空間の意味を了解したとき、
ずいぶん強引な概念だなと思った記憶があります。
同等な機能を持つもっと素直なものがあってもよさそうな気もしましたが、
他の定式化をしてみろと言われても困ります。
りあえず例として、関数空間を使わないラグランジュ方程式の導出を上げてみます。定積分
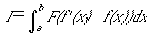 (2)
(2)
を最小化する関数f(x)を求めよというのが典型的で古典的な変分問題ですが、
(2)からラグランジュ方程式を導くために関数空間を利用するような説明を読んだおぼえはほとんど
ありません。その中で最も上手い説明だと思ったのは、
テスト関数を実数αでパラメーター付けするやり方でした。
(2)を最小化するf(x)を計算するためには、答えとなるf(x)が目的のものであることを確認するために、
f(x)から少しだけずれた沢山のテスト関数について定積分Iの変化を見てやる必要があります。
もしf(x)と少しだけ違うテスト関数を実数αでパラメーター付けすれば、
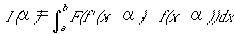 (3)
(3)
となります。ふつう(3)の定式化では、f(x,α)のα=0において解関数f(x)=f(x,0)に
なると考えます。そして関数fの変分δfを、
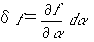
のことだと定義します。こうすると定積分Iを最小化する関数f(x)を求めよという性格の悪そ
うな変分問題が、定積分Iを実数αの関数I(α)と考えることができて、
いつのまにか通常の微積分問題に化けてしまいます。実際に積分記号化の微分と部分積分の公式を利用して、(3)の∫の中を処理すると、本当にラグランジュ方程式を導けます(ゴールドスタインの古典力学より)。
これなどは、関数空間を使わなくてもそれなりのことはできるんだぞ
、という格好の例だとは思うのですが、もし問題の正直な意味を考えるなら、
この方法は少々卑怯です。この方法のみそは、パラメーターαによって、
じつは解関数f(x,0)とテスト関数f(x,α)の距離を計っているところにあります。
そう考えると、定積分Iは実数αの関数I(α)ではなく、
関数fを変数とする汎関数I(f)だとみなすべきで、
f(x)=f(x,0)を含む解集合に関数間の距離を定義できたのなら、
それは変分問題のやはり最も正直な定式化であると感じます。
このように関数空間が考え出された根っこには、任意の集合に距離の導入したい!
という衝動が働いていたように思われてしかたありません(個人的意見です)。
この後、数学者と数学に関わる人達に関して一部過激な発言がありますが、
アマチュアの世迷い言ということでご容赦下さい。他意はありません。
3.関数空間への長い道のり
関数空間が考え出された根っこには、任意の集合に距離の導入したい!という衝動が働いて
いたと仮定します。そうすると、距離を導入するためには目的のものを含む集合を想定し、
その集合を何らかの意味での線形空間と考え、計量テンソルを入れて内積を定義するという手順が、
私の知る限りではのふつうの方法です。
もっともその集合に距離付け可能な位相を入れられるとしてですが・・・。
距離付け問題は難しすぎるので、ここではこれ以上一言も申しません。
とにかく、何らかの意味での線形空間と考えるわけですから、
関数の集合も線形空間と考える必要に迫られます。ところが線形空間(ベクトル空間)
とベクトルそのものとの区別もつかず、ベクトルとは必ず2次元の矢線ベクトルのことだと思い、
矢線ベクトルと位置ベクトルの違いさえもわからなかった、当時の私の前に現れた関数空間の定義とは、
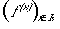 (4)
(4)
なるものでした・・・。はたまた、
RR
・・・てなもんでした。はっきり言って、絶望的気分になりました。
それでも色々と本を読みまわすうちに、(4)の表現は、
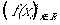 (6)
(6)
としても良いらしいことが漠然とわかってきました。
(6)の形までくると点列というか、漸化式との不正確な類推
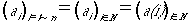
から、次のようなイメージが沸きました。ただし当時の私は、
矢線ベクトルと位置ベクトルの違いもわからず、実質的にベクトルといえば2次元の位置
ベクトルの事だと頭から信じ込んでいたので、沸いたイメージもその通りのものです。
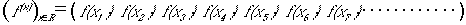 (7)
(7)
このイメージは正しいと思います。
各x=xiにおける関数値f(xi)を一列に並べたベクトル。それが
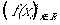 の意味だ。ここで問題になるのは、xiとxi+1が実数の隣り合った点というてんです。
当然x=xiは、昇順に並んでると仮定してます。するとx=xiとx=xi+1が隣り合った点なら、
こんな番号付けはどうやった行うんだ!。
xiとxi+1の距離は正確に0なんだぞ・・・。
xi+1がxiとよりちょっとでも大きいことはどうしてわかる?。
の意味だ。ここで問題になるのは、xiとxi+1が実数の隣り合った点というてんです。
当然x=xiは、昇順に並んでると仮定してます。するとx=xiとx=xi+1が隣り合った点なら、
こんな番号付けはどうやった行うんだ!。
xiとxi+1の距離は正確に0なんだぞ・・・。
xi+1がxiとよりちょっとでも大きいことはどうしてわかる?。
こういうことやるために数学者達は無限集合論を開発したのだと、勝手に納得しました。
実際Cardinal(R)なる無限基数があったではないか(立ち読みした本で見ただけ)。
「Cardinal(R)の細かさで番号付けすれば、xiとxi+1のは区別できるのだ」と勝手に納得しました。
しかし距離が本当に0のところで順序をつけられるのでしょうか?。
このあたりの矛盾を論破されたのが、田村祐三の「数学の哲学」だと個人的には思っていますが、
(7)の表現は正しいと思います。
こういうことができるとした強さこそ、無限集合論の価値ある暴走なのです(ほんとか?)。
よし、(7)は正しいとしよう。「・・・」も含めて。「・・・」はふつう可算無限にしか使わないが、
無限集合論があるから、「・・・」を連続無限に使っても大丈夫だ。アマチュアはそれでいいいのだ。
次に(7)によって、本当に関数を定義できるのか?という疑問がありました。
当時の私は関数といえば、
y=x2
とか、数式で表されるような関数しか知らなかったのです。
それがいきなり(7)のような形でy=x2を表せるのかという、
根本的アマチュア的発想がありました。
表せるのですね。このような疑問が沸いたのは、関数値と関数そのものとの区別を
知らなかったからです。
(7)の立場で言えば、
「任意のxでの関数値f(x)全てを言えるのだから、それは関数f(x)を知ってるのと同じだ」となります。このとき初めてy=f(x)とは、
f(x):R → R
と書かずに、
f:R → R
と書くのですね。関数値と関数を厳密に区別していたわけです。
そんなことさえ知りませんでした。それまでは、
y=f(x)を平気でy=y(x)とかに書きかえてました(記号の節約とか称して、いまでもやりますが)。
ともあれ、(7)のイメージを了解できれば、任意の関数は原初的イメージとして、
直交座標無限次元空間の1点として表されることを了解できます(ヒルベルト空間?)。
4.(7)がベクトルであることを確かめる(そんなの明らかじゃないか!?)
次に現れた難問がこれです。どんな本を読んでも(7)の形式で表された関数に対して、
和と定数倍を定義できることを確認します。(記号の節約とか称して、(7)を次の(8)に書きかえます)
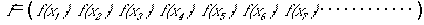 (8)
(8)
原初的のイメージとしては、(8)の形式で直交座標空間の1点として表された関数に対して、
何をいまさらベクトルであることを確認する必要があるのか?となります。
当時の私は実質的に、ベクトルといえば2次元の位置ベクトルの事しか知らなかったのです。
よってカルテシアン表現されたものは全て、明らかに位置ベクトルでした。
しかし関数解析とか位相解析とかのどんな入門書を読んでも、ベクトルであることを確認する、
和と定数倍の定義の部分は必ず出てきます。しかも数行で終わります。
最初は明らかとして無視していました(数行で終わるし)。
が、余りにも必ず出てくるので悩み出しました。必ず出てくる理由はなんだろう?。
例を上げます。
擬ベクトルはベクトルか?という問題があります。現在の私は、
擬ベクトルもベクトルであると躊躇なく答えますが、それは擬ベクトル空間がベクトル
空間の公理を全て満たすからです。擬ベクトルは一定の方法で、土台となるベクトル空間から
定義されますが、擬ベクトルはベクトルか?という問題の本当の本質は、
土台となるベクトル空間から定義された新たなベクトル空間としての擬ベクトル空間が、
土台となるベクトル空間とはたして同一なものなのか、という点にあると思います。
考えれば明らかですが、初学者は非常に悩みます。
なぜならどっちも、カルテシアン位置ベクトル形式で書かれるからです。
いまの場合も同じです。(8)のように関数が位置ベクトル形式で書けたとしても、
それがベクトルかどうかは要確認です。いまの場合、土台となるベクトル空間は位置ベクトル空間で、
それを概念的に拡張した関数空間で、土台となる位置ベクトル空間のベクトルの和と定数倍を
そのまま使用できるのか?という話だと思います。
擬ベクトル空間と土台になるベクトル空間の関係では、
土台になるベクトル空間での任意の基底変換変換式が、擬ベクトル空間でも使えるのか?
という点がポイントになります。使えるのは、反転を含まぬ直交変換のみでした。
幸いなことに、概念上土台となるベクトル空間である位置ベクトル空間の和と定数倍は、
もし関数空間を位置ベクトル空間とみたてた場合の、関数ベクトルの和と定数倍に
自然にそのまま流用できます。
もし自然に流用できなかったら、概念上土台となるベクトル空間である位置ベクトル空間の和と
定数倍に対応するものを、関数空間のほうで新たに定義する必要があったのではないか?。
そこまで考えて、この難問をやっと了解しました。
(・・・正しいんだろうか?)
5.関数空間に内積を定義しようとした
さて。関数空間が線形空間であることは証明できました(ほんと?)。
例えば変分問題における解集合の関数空間に距離を入れるには、あと内積を定義するだけだ。
関数とは、直交座標無限次元空間の位置ベクトルとしての1点だった。関数fとgの内積とは、
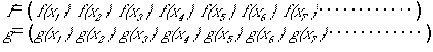
だから、
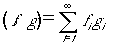 (9)
(9)
に違いない。ここで、fi=f(xi)でありgi=g(xi)。
なんかすごく自然で安心します。
でも(9)を計算してみると、ふつう・・・・・・発散するじゃねぇ~かよ!。
有限の大きさのfi・ giを無限個足すからです。
そこで数学者達は、距離とは何か、内積とは何かについて、ちょっとだけ反省しました。
どうしてちょっとだけかというと、反省の直後にまた暴走し出すからです。
6.距離関数の恣意性
もっと根本に戻って、距離を定義するにはどうしたらいいでしょう?。
田村祐三の「数学の哲学」によれば、距離を計るには二つの図形を重ねられる操作可能性が必要と
書かれています。リーマンもその就任公演で、同様の事を言ったと彼は書いています。
要するにナポレオンが造った「メートル原器」が必要なのです。
「メートル原器」という任意に決めた単位長さと、任意の長さとを比較することによって
距離は決まります。ここで「メートル原器」の決め方は、全くの任意です。
言いかえれば距離の単位はア・プリオリには決められず、
もっと一般的に距離関数には無限の恣意性があります。距離関数の定義は次のようなものでした。
1.d(x,y)≧0,xとyはその間の距離を計ろうとする2点(← この意味はどうとでもとって下さい).
2.d(x,y)=0は、x=yに限られる.
3.d(x,y)+d(y,z)≧d(x,z)(三角不等式).
この制限を満たす限り、その間の距離を計ろうとする2点間の距離値には、
任意の実数を当てて良いということになります。ただし距離関数の定義3.から、
より遠い距離にはより大きな実数が当てられますが、そのような整合性を守る限り、
距離関数(と距離値)には無限の恣意性があります。
最も良い例が、単位の変更です。さっきの「メートル原器」は現在の1mにかなり
近いものと思いますが、
現在のメートル単位系で1kmの「メートル原器」を造って、
それを1mと呼んでも距離関数の制限には、何の抵触もないはずです。
現在のメートル単位系で1kmの「メートル原器」を単位長さ1mとして長さや距離を計ったら、
現在の1mは1mmとなるだけで、理屈の上では何の不都合もないはずです
(設計屋である私は大いに困りますけど)。どうしてこんな事をして良いのでしょう?
「距離関数は、不変な物理距離に対して、「メートル原器」によって決められた数値を割り 当てるだけ」だからです。現在の1mを1mmとするのは、1000倍大きな単位を採用した結果にすぎない、 ということになります。ここで言いたいことは、
「どのような距離関数を採用しようと、物理距離そのものは変わらない」という発想があったのではないか、というてんです。つまり距離関数は、便利なものを選べば良い。
7.距離関数と内積の同値性
ある集合に距離を導入することと、内積を導入することは同じではないでしょうか?。
実際、内積を定義できれば、ベクトルの2乗ノルムによって2点間の距離を定義できます。
逆にある集合に距離を導入できれば、三角形の3辺の長さを定義できるので、
余弦定理が意味を持ちます。そして内積とは、余弦定理の座標表現によるいいかえです。
実際、内積を不変に保つ線形変換は直交変換に限られますが、逆に等長線形変換は内積をも不変に保ち、
直交変換に一致してしまいます。
最も単純に言えば、内積は三角形の3辺の長さとその内角との関係を一意に与えるものなので、
距離を与えれば、内積も自然に定まるということです。
もっとも計量テンソルの選び方で内積の定まり方には、またも恣意性が入ってきますが、
それは直交基底を選ぶのか、斜交基底を選ぶのかといった趣味(または便利さを考慮した)
恣意性であって、原則的には、距離関数を選べば内積も自然に定まるというのが、個人的意見です。
8.関数空間に内積を定義する
関数とは直交座標無限次元空間の位置ベクトルとしての1点である、と考えた場合、
最も自然な内積は、
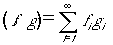 (10)
(10)
でした。ただし(10)は、発散という死に至る病を持っています。
ここで6.より、内積を与えることは、距離を与えることと同じだという事実(?)を思い出すと、
(10)が発散して死んでしまう理由は、じつは距離の与え方がまずいからだ、となります。
そして5.より「距離関数は、便利なものを選べば良い」のです。
いま最高に不便なのは、最も自然な内積と思われる式(10)が発散することです。
よって、発散しないように距離関数を選べば良いのです。
5.で行った単位の変更を行います。式(10)の単位系は不明ですが、
の不明な単位系をh倍大きな単位系で書いた姿だけは、すぐにわかります。
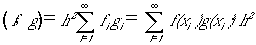 (11)
(11)
です。単位変更前の(f,g)は、発散する危険を伴っていたのですから、
hは無限小の大きさでなければなりません。
これは最初の距離値が0に見えるくらいに、大きな単位に変更したと言っても同じです。
最初の距離値が0に見えるくらい大きな単位系を採用することによって、式(10)は収束します。
こうしても良い理由は、
「どのような距離関数(単位)を採用しようと、物理距離そのものは変わらない」からです。ここで物理距離とは、直交座標無限次元空間が存在すると仮定した場合の、 直交座標無限次元空間における2点間のユークリッド距離です。 さらに、最初の距離値(無限大)が0に見えるくらいに大きな単位とは、 無限に大きな単位系でなければなりません。
9.区分求積
式(11)の最右辺で、h2=dxとします。ここでdx~0であり、
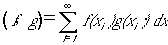 (12)
(12)
となります。式(12)の右辺は、昔懐かしき区分求積の形をしています。
細かい話を無視すれば、これはリーマン積分の原形です。
ルベーグ積分まで行くともっと精密な話になりますが、
全ての原形は式(12)の区分求積にあると思います。
関数fとgの定義域が[a,b]なら、dx=(b-a)/n,xi=a+(b-a)/n×(i-1)であり、
nは任意に大きな自然数で、最後の形は、
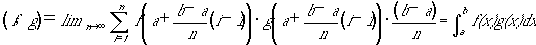 (13)
(13)
となります。こういう形でしか、私は関数の内積を納得できませんでした。

| NO.1119 | 2002.1.1. | 水の流れ | ある不等式の証明(5) |
さて、NO.1108(2)はグラフの利用や「左辺-右辺」をしないで書いてありますが、
高校生には、やはり利用して解かせたいです。
なお、この不等式には、人の名前がついています。
ジョルダンの不等式と言われていますよ。
では、グラフで証明します。
f(X)=sinx とおくと、f’(x)=cos(x) f’’(x)=-sinx で0<x<π/2 より
f’’(x)=-sinx <0
したがって、f(x)は上に凸である。
2点(0,0)と点(π/2 ,1)を結ぶ直線はy=(π/2) x だから、
グラフを描けば明らかに
y=f(x)=sinxのグラフは直線y=(π/2) x より上にある。
証明終わり
次に、g(x)=sinx/x 、g(0)=1 とおく。
| g’(x) | =(1/x2)[x・cosx-sinx] |
| =(cosx/x2)[x-tanx] |

| NO.1120 | 2002.1.3. | 水の流れ | 交代級数の和 |
今、オイラーの書いた「無限解析入門」という本が手元にあります。
ここの中に次のような無限級数の和を求めています。
皆さんも、考えてください。
ただ、オイラーの足下にも及ばない太郎さんにとって、ある無限級数を関数として考えました。
問題
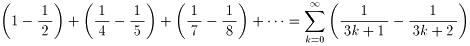
ここで、
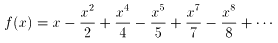
とおいて考えてください。

| NO.1121 | 2002.1.4. | 渡部 勝 | 折る紙の数学 |
有限な平面(X軸及びx=a Y軸及びy=bに囲まれた平面)
内における直線(線分)の持つ性質について色々考えてみました。
すると無限な平面においては、判らなかった面白さに出会ったのです。
例えば、その比をNとして、各々の中点と中点を結ぶ直線を考えてみます。
この時、この直線を対称な軸とする、少なくても1つの頂点の位置は
このaとbを各々 (N×N) / (1+N×N)に分割するのです。
この有限な平面をペーパーに見立て、その面白さの一部を、
書きましたのでご覧下さい。
『折る紙の数学』 講談社ブルーバックス

| NO.1122 | 2002.1.5. | yokodon | ある不等式の証明(6) |
DDTさん、NO.1111 の方針は思いつかなかったです。
なるほど、お見事です。
一つ気がかりがあるとすれば、
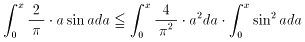
の部分ですが、この不等式の右辺の各々の積分の被積分関数は積分区間上で非
負なので、以下を理由に結局正しいですね。
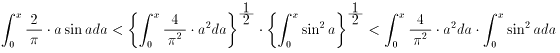
水の流れさん、
不等式の名称は存じ上げませんでした。御教示有り難うございます。
ただ、今回の問題提起に当たっての個人的な問題意識を多少申させてください。
本問はグラフで解く方が視覚的に分かりやすいし、「(左辺)-(右辺)」の微分
で単調性を主張する方が取り組み方としては実行しやすい。それは確かです。ただ、
(高校生の時以来)常々思ってきたことなのですが、
Q1:「図より明らか」って本当?
Q2:三角関数の微分の応用による不等式の証明に、一種の循環論?が見られる場合が
存在すること
などの“相克”をどうしたものか?と言うのが、僕にはあるのです。
#尤も、それを言ってしまうと、「積分計算の実行で微分積分学基本
定理を使うのだから、今回の問題でも元の木阿弥」と言ってしまえ
ばそれまでなのですが。
現在は、三角関数の定義(というか導入)の仕方を工夫することによってこの問題
が解決可能であることを知っていますが、それを高校生向けの教育でどうする?とい
うのが、少々悩ましいところです。
何のことだか分かりにくいと思うので、具体的な問題で考えてみましょう。
以下の問いに対する答えが正しいかどうかを、釈迦に説法とは存じますが、ちょっ
とお考えいただければ幸いです。
問題:以下の不等式の成立を証明せよ。
0 < x において、sin(x) < x
解答1:
f(x) = x - sin(x) と置く。
f'(x) = 1 - cos(x) ≧ 0( 0 < x )であるから、f(x) は単調増加。
故に、f(x) > f(0) = 0 より主張は成り立つ。
解答2:
半径1の円周上にて、中心角 x (0 < x)なる扇形と、(扇形の内部にあって)
半径を斜辺とする直角三角形を考える。
両者の面積を比較すれば、1/2・x > 1/2・sin(x) であるから、明らか。
上記の『解答1』に関して、「三角関数の微分の公式を導くのに、x→0 のとき
sin(x)/x →1 であることを活用している以上、その極限値の計算を正当化する論拠
(の一部)が“0 < x において sin(x) < x < tan(x)”であることを既に使って
いる。だからこの解答だと結論先取りになってしまう」という批判は、高校で数学の
教育に携わっておられる方でしたら、恐らくお聞きになったことがあるでしょう。
そこで、この“0 < x において sin(x) < x < tan(x)”をどうする?というと
ころで、高校の範囲だと上記の『解答2』の様に「直角三角形と扇形の面積の比較」
で解決し、“x→0 のとき sin(x)/x →1”の極限計算は「一般角における三角関数の
拡張を以て x →±0 の場合の極限を導く」ことで済ませているわけですが、はて、
では何故そのような大小の比較が可能なのか? そりゃあ、絵を描いてみれば一目瞭
然ではあるのですが、ここで問題にしたいのは「『図より明らか』の図が正しいこと
を、どうやって説明するのか?」です。
#勿論、視覚的な理解を軽視するわけではなく、自分が理解してい
る…はずの…図の正当性を、論理的にどう説明するか?を問題にしているわけです。
「それをいっちゃあ、中学で習う三平方の定理はどうする?」
というご批判も予想しております。
高校時代、同級生に同じことを言ったら「どうしてじゃなく
て、そうなるんだよ」としか言い返されなかったのを、今で
も覚えています。
今回の「ジョルダンの不等式」の場合、例えば、sin(x) の凸性を利用して図で説
明するものとして、その凸性を微分を使わずにどうやって説明すればいいのでしょう
? また、両辺の差で作った関数を微分して示すものとして、これは上記の結論先取
から抜け出ることが、果たして予め出来ているのか? 余りに単純な形の式なので、
その辺が多少気持ち悪いと思ったわけです(単なる勘違いだったり、或いは考えすぎ
だったりするかも知れませんが)。
今回提起した「積分のコーシー・シュワルツ不等式の応用による、ジョルダンの不
等式の証明」は、sin(x) の微分の公式や既知のグラフを前提に置いてしまえば易し
めの演習問題です。が、何を前提にして何を導くのか?についてちょっと考えると、
実は袋小路に填りそうな深みのある何かを指し示してはいないだろうか?…こんなこ
とを、ちょっと思ったわけです。そうしたわけで、「式の証明は式のみで行えれば理
想的だなぁ」と思って、袋小路を上手く抜けられそうな試案をひねり出してみたわけ
です(と申しましても、実は別のヒトから「解いてくれ!」と持ってこられた代物だ
ったのですが)。
#どこぞの教育学部の論文試験で、出たりして(出ない出ない)。

| NO.1123 | 2002.1.5. | yokodon | 関数列の極大点(1) |
模試シリーズ8
数列{an}(n = 1,2,3,...) と関数列{fn(x)}(n = 1,2,3,...) に関して、
以下のような関係及び条件が成り立っているものとする。
A:fn(x) = (n - x)n・(x - an)
B:a1 = 0
C:fn(x) は x = an+1 で極大値を取る。
(1)a2, a3, a4 の値を求めよ。
(2)数列{an}の一般項 an を n の式で表せ。

 E-mail
E-mail
 戻る
戻る