Weekend Mathematics/コロキウム室/NO.151
コロキウム室
| NO.1278
| 2002.9.13. | 浜田 明巳 | tanθの値を求めよ(5)
|
受験数学での約束,その他諸々
受験数学の問題を解く際には,いろいろの約束事や,暗黙の了解があります.思いつく限りでは,
(1)解が2つある場合,その2つの解が重なる,つまり重解になる場合も含む.絶対に2つになる,という場合には,異なる2つと書かなくてはならない.
(2)関数式を求めるとき,問題にそう書いてなくても,定義域も求める.
(3)不等式の証明において,問題にそう書いてなくても,等号が成立する場合を求める.
(4)最大値,最小値を求めるとき,問題にそう書いてなくても,そのときのxの値も求める.
(5)不等式,無理方程式を解く場合,使用される文字は,問題にそう書いてなくても,実数とする.
(6)解を求めるとき,問題にそう書いてなくても,解が存在する事から求めなくてはならない.今回私が問題にしている場合ですね.
(7)証明は,1歩前の段階から始める.例えば,
(sinx)'=cosx
を使って,
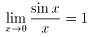
を証明してはならない.なぜなら,(sinx)'=cosxは,
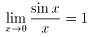 を使って証明される事だから.
を使って証明される事だから.
等です.もし他にも思いついたものがあれば,お知らせ下さい.
興味深いものが出来上がると思います.
考えてみれば,(1),(2)は当然でしょう.
(3)はどうでしょうか.A≧Bを証明せよ,という問題では,それを証明するだけでいいような気がします.教育的見地から見れば,A=Bとなる場合を考える事は勉強になりますので,やった方がいいです.でもそれは証明せよという問題とは多少異なる問題です.ですから,この手の問題では,等号が成立する場合も求めよ,という但し書きを最後に書いて欲しいと思います.
(4)はどうでしょうか.これも最大値,最小値を求める事と,そのときのxの値を求める事は,多少異なる問題のような気がします.但し書きを最後に書いて欲しいところです.もっとも,この問題の型式は,yの値の範囲を求めるのと似ています.したがって,最大値,最小値を求めよ,という問題では,そのときのxの値が必要であり,値の範囲を求めよ,という問題では,xの値は必要ない,と解釈出来なくもありません.
(5)は,少なくとも私の受験生時代(20年以上前)には,そう言われました.しかし,最近はそうでもありません.不等式の問題で,文字が虚数の場合を考えさせる場合がありました.問題の条件として,最初に断っておいて欲しいところです.これは時代の変化というところでしょうか.
(7)は微妙です.授業の展開としては,当たり前の話です.しかし,実際の入試問題で出題される場合,授業とは無関係なのですから,どんな方法で証明してもかまわない気がします.
勿論,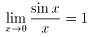 を使って,
を使って,
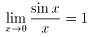 を証明するなんて,とんでもない場合を除いて,ですが.もしかすると,
を証明するなんて,とんでもない場合を除いて,ですが.もしかすると,
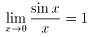 を使わないで,(sinx)'=cosxを証明した人がいるかも知れません(そんな事はないか).採点担当の先生の話を聞く限りでは,例外なく,だめ!という事なので,生徒に指導するときは,ちゃんと言います.
を使わないで,(sinx)'=cosxを証明した人がいるかも知れません(そんな事はないか).採点担当の先生の話を聞く限りでは,例外なく,だめ!という事なので,生徒に指導するときは,ちゃんと言います.
これら以外に,こんな話を聞いた事があります.
(8) x(x−1)2=0の解は,x=0,1ではなく,x=0,1(重解)と書くべきである.
解集合を考えれば,重解とそれ以外の区別は重要ではない,と思います.ところで,sinx=1の解はどうなるのでしょうか.重解でしょうか.
数学ではないですが,算数の授業で,
(9) 10÷3=3・・・1であって,10÷3=3・・1とか,10÷3=3・・・・1ではない.こう書くと×になる.「・・・」は「あまり」という意味であるので,点は3個である.
というのを,生徒から聞きました.論外でしょう.
さて,(6)です.こういう風に考えてみました.
問題文が間違っている.または,解が存在しない.
→ 問題の仮定が矛盾している(ここら辺,ちょっと苦しい).
→ 矛盾した仮定の元では,何を結論づけても真である.
例:命題「1=0ならば,1=2である」は真です.
→ 何を書いてもいいのだから,書かなくてもいい.
→ 解が存在しない場合は無視して,解が存在する場合のみを書くだけで十分である.
→ 「tanθの値を求める」問題において,cosθ=0の場合は無視してよい.
実際に生徒が受験する事を考えると,こんな指導をしてはいけません.
しかし,純粋な数学としては一理あるのではないでしょうか.
解なしが答の場合,その問題の仮定を満たすものが存在しない事になります.つまり,仮定自体が矛盾しているのです.したがって,その仮定から何を導き出しても,どんな矛盾する事を書いても,結論として論理的に矛盾しない.したがって,そんなときは「問題にミスがあった」という事で,全員に点をあげる事になるでしょうが,それは数学的に正しい事なのです.つまり何を書いても,無解答でも,真なのです.教育的配慮に欠けるとか,いろいろと問題があるでしょうが,数学的には問題がないのです.
でも,昨今の入試問題の作問ミス,採点ミス,集計ミスのニュースを聞くと,そんな親切には学校側が対応してくれないのではないか,対応してくれるとしても時間がたった後だったら意味がない,なんて考えてしまいます.やはり最低限,きちんと出来る限り書いておいた方が無難なのでしょう.
とにかく,全力で生徒を指導すべきですね.教室にはガウスがいます.皆さん,アドバイスを頂き,どうも有り難う御座いました.

| NO.1279
| 2002.9.13. | 中川 幸一 | ぞろ目(6)
|

>を満たす、自然数n、pおよび、一桁の自然数mが
>n≧6(あたりで)存在しないことを示せばいいわけで
ここのn≧6と考えた理由がわかりません。
教えてください。
という質問をBossF(^O^)にしたところ
、以下のような解答が帰ってきました。
これは、実際取り組んでいただくとわかると思いますが、繰り上がりの問題を、
繰り込んで解決するためには例えば上3桁でいこうとすると、その倍はとらねばならないのです。
で、前回の試しに7桁ぐらいまでは簡単にいけたので、
ひとつの目安に6桁としたのです、
問題は繰り上がり分をどう評価してnの範囲を狭めていくかなんですけれどね
まず、必要条件を考えます
右辺左辺は(1)の右辺左辺とします。
さて、連続数の積を眺めてみると(1)の左辺は
n=0のとき 9・0・1≡0 (mod 10)
n=1のとき 9・1・2≡8 (mod 10)
n=2のとき 9・2・3≡4 (mod 10)
n=3のとき 9・3・4≡8 (mod 10)
n=4のとき 9・4・5≡0 (mod 10)
n=5のとき 9・5・6≡0 (mod 10)
n=6のとき 9・6・7≡8 (mod 10)
n=7のとき 9・7・8≡4 (mod 10)
n=8のとき 9・8・9≡8 (mod 10)
n=9のとき 9・9・0≡0 (mod 10)より、
より、
0≡9・0・1≡9・4・5≡9・5・6≡9・9・0 (mod 10)
4≡9・2・3≡9・7・8 (mod 10)
8≡9・1・2≡9・3・4≡9・6・7≡9・8・9 (mod 10)
よって
(左辺)≡0,4,8 (mod 10)
また、このとき(右辺)は
(右辺)≡2m(10p-1)≡2m・10p-2m≡-2m (mod 10)
m=1のとき -2≡8 (mod 10)
m=2のとき -4≡6 (mod 10)
m=3のとき -6≡4 (mod 10)
m=4のとき -8≡2 (mod 10)
m=5のとき -10≡0 (mod 10)
m=6のとき -12≡8 (mod 10)
m=7のとき -14≡6 (mod 10)
m=8のとき -16≡4 (mod 10)
m=9のとき -18≡2 (mod 10)
ここで、(右辺)≡0,4,8 (mod 10)
となるのは、m=1,3,5,6,8
よって、
n(n+1)=111…10、222…2、1333…32、666…6、1777…76
となることが必要条件である。
このことを念頭に置きながらこの前のUBASICでのプログラム
を見てみると、

190 のdateが1,3,5,6,8となっているのが分かると思います。

| NO.1280
| 2002.9.15. | DDT | 疑問に思うこと(2)
|
いきなり「問1の答は、「問1.問1の答」で良いか?」では難しいので、問題をもっと小さくしてみます。
[1] xを整数として方程式x2−2x+1=0の解は、x=xで良いか?
[1] において、xはx2−2x+1=0を満たすものとして仮定されているので、xの解であるxは明らかに、条件x2−2x+1=0を満たします。これはこれで文句は付けられないように見えますが、これを認めると任意のaを[1]の解とできます。
x=aが[1]の解であることの検算
aがa2−2a+1=0を満たせば良い。x=aなのでx2−2x+1=0である以上、a2−2a+1=0は当然.
x=xは「問1.問1の答」に相当し、x=aは「問1.問1の答になるもの」とでもした時に相当すると思います。ところでaは任意だったので、例えばaが2でも良いはずです。このとき先の検算は、
x=2が[1]の解であることの検算
2が22−2・2+1=0を満たせば良い。x=2なのでx2−2x+1=0である以上、22−2・2+1=0は当然.
となります。「ちょっと待て!、22−2・2+1=22−22+1=1で、1=0は当然となるから、これは変だろう!」という反論は、x=xを解とみなす立場では無意味です。
x=2が[1]の解であることの検算をこの立場の精神に則って普通の言葉に翻訳すれば、「x2−2x+1=0を満たす整数xを記号2で表わした」ということになると思います。気持ちまで含めて書けばx=2とは、「問1.問1の答は2(問1の解を記号2で表わした)」です。だから、正しくは(普通の解釈では)解無しの場合さえも、正解を書けます。
[2] xを整数として方程式x2−3x+1=0の解は、x=2.
x2−3x+1=0の解は、あったとしてx=1/2×(3±51/2)なので普通には解なしですが、記号2は[2]の条件を全て満たすある対象を指示するものとして導入されたので、x=2が解です。この対象は"空"かもしれません。それが解無しを表わします。「しかし整数2は、[2]のような条件を満たさないはずだ」という反論もやはり無意味です。だから[2]に現れた記号2は、整数でなくて記号です。例えば整数を表わすのには普通、1,2,3,・・・という記号を用いますが、それは十進表記とアラビヤ数字の使用が慣習になっているからで、1,2,3,・・・が記号である以上、別の記法を用いても整数理論は成立します。整数2を記号2で表わせという決まりも論理的にはないはずです。このようにx=xを解とみなす立場では、予想に違わず問題は常に恒真式x=xの同語反復で、矛盾はないのですが、問題の外部と没交渉です。
このような事態を避けるには、別の立場の導入が必要です。明らかにそれは、= の使用法に関わると思われます。「数学の哲学.pp108〜109,田村祐三,現代数学社1981年」に、以下のような話があります。
等号関係は、対象間で成立するのか、対象を指示する記号間で成立するのかについては、けっこう昔から議論のあったところだそうで、結論から言えば意外なことに、等号関係は記号間で成立すると解釈するのが、普通には正しいという意見です。[2]のような事態が起こるのは、まさに記号2と記号xの間で等号関係が成立する、としたことによるように見えますが、[2]でx=2とおけるのは、問題の条件を全て満たす対象を指示する記号として2を定義したからで、その対象が、xで指示される対象と同じなので等号関係が成立します。つまりx=2とおける根拠は、対象間の等号関係の成立にあります。
これこそ等号に関するふつうの考えのように見えますが、一方記号間に成立する関係だとするとどうなるでしょう?。引用すれば、
「フレーゲによれば、記号(名前)は指示対象を指示すると同時に、意味を表現し、その意味には対象の与えられ方が含まれている」
とあります。現在では、意味は対象の与えられ方から発生するとみなす傾向が強いですが、これを認めると、さっきの話が逆転します。
等号関係は、記号間で成り立つとします。[2]の条件「xを整数としてx2−3x+1=0が成り立つ」も記号間で成り立つ関係になります。よって「整数xという意味」は「記号xの与えられ方」から発生しているので、自動的にxは整数理論を満たすことが必要になります。そこで逆解析的発想で、整数を生成するペアノ公理系に根拠をもつ四則演算を駆使して完全平方変形を行い、「二次方程式x2−3x+1=0を、整数の系列に埋め戻す」ことを試みます。
「等号関係は記号間で成り立つ」とすることで、与えられた問題条件に、それが依存する外部理論との整合性はあるのか?という問題が逆に発生し、外部理論との交渉も発生して、その確認を取るために「解く」という行為が生まれることになります。個人的にこれは、とてもまっとうな意見だと思いました。以上の話が一般的にも成り立つのであれば(成り立つと思えるのですが)、等号関係がどこで成立するかは、常識的感覚とはまるで逆です。対象と記号,記号と意味に双対関係があるのかと疑ってしまいたくなる程です。
これを「問1.問1の答」に引き戻して考えると、記号「問1.」と記号「問1の答」にも、その与えられ方が存在し、与えられ方間の整合性問題が発生します。ところでその与えられ方ですが、記号xや記号2とは比べ物にならないくらいに大きな文脈依存であるはずです。日常言語ですから。事実上、整合性問題は片付かない。よって「問1.問1の答」は、少なくともその検討が成就されない間は不可!。
しかし、いずれにしろ微妙な話です。等号関係は対象間でか記号間での成立か?、などという話は相当に普通の数学からははみ出しています。学生に「数学も外界とは無関係にはやっていけないのよ」と説教臭く話して嫌われるよりは、やっぱり「常識的にやってね」と言うしかないんでしょうか?。

| NO.1281
| 2002.9.14. | 母神のこねこ | 四角錐台の体積
|
仕事の関係で四角錐台の体積の公式がなぜ以下のようになるのか
教えて下さい。
h{(2a+c)b+(2c+a)d}/6
a,bは下の底面の長方形の辺、c,dは上の底面の長方形の辺の長さです。

| NO.1282
| 2002.9.15. | にゃんこ(二暗刻) | コラッツの問題
|
小生はリタイヤして毎日の暇をソフトつくりや算数?で楽しんでいます。コラッツの問題が未だ証明されていない?と知り、2ヶ月ばかりの間挑戦しました。その結果、意外な発想は出てきませんでしたが、平凡なありきたりの方法で一応証明が出来上がりました(8/15)。完全と言えるかどうか判りませんが、ご高覧のうえ、後批評頂ければ幸いです。
その後インターネットであちこち視ていたら、小生と考え方は異なりますが、証明されているのを発見し(下記)、ちょっとがっかりしました。
「数学の部屋」
「角谷の予想」
この2件の証明はこれから勉強させて頂きます。
コラッツの問題(数論の未解決問題)
「正の数 n をとり、これが奇数なら3倍して1を加える。偶数なら2で割る。
これを繰り返すとはじめにどんな n を選んでも、いつかは 1 → 4 → 2 → 1 を繰り返す」
n が 4兆まではコンピューターで確かめられている。
(富永裕久著 フェルマーの最終定理 1999-11-30 (株)ナツメ社)
A-1. この問題の証明を試みるにあたり、正の整数 n0 を考える。
条件による処理後の値を nj (j:処理回数)とする。
但し、3倍して1を加えるのも、2で割るのも、共に1回の処理と数えるものとし、
ここで扱う数値を表す文字は特に断りをしない場合は全て正の整数とする。
(1) n0 = 4 のとき
n1 = n0 / 2 = 2
n2 = n1 / 2 = 1
n3 = 3n2 + 1 = 4
これで 4 , 2 , 1 , 4 , 2 , 1 が繰り返されることは確認できる。
(2) n0 が偶数のとき h を奇数とすれば
n0 =h・2p と表せる
n0 を p 回( 2 で割る)処理をすれば np = h (奇数)となる
np = n0/2p = h < n0
h = 1 なら 成り立つ 。その他は奇数の場合で検討する。
(3) n0 が奇数のとき
n0 = 2m - 1 と表せる
m が 2 を約数として持つならば(偶数ならば)
k を奇数 として
m = k・2a , n0 = k・2a+1 - 1 と表せる
この奇数を 3 倍して 2 で割る処理を a+1 回して n が n2a+2 になるとすれば
n1 = 3(k・2a+1 - 1) + 1
| n2 | = n1 / 2
|
| = { 3(k・2a+1 - 1) + 1 } / 2
|
| = k・31・2a - 1
|
a は正の整数だから n2 は奇数となり
| n4 | = (3n2 + 1) / 2
|
| = { 3(k・312a - 1) + 1} / 2
|
| = k・32・2a-1 - 1
|
| ・・・・・・・・・・・・・・・・・・・・・・・・・・・
|
| n2a+2 | = (3n2a + 1) / 2
|
| = k・3a+1- 1 ・・・・ (1)
|
となり、n2a+2 は偶数となる
n2a+2 - n0 = ( k・3a+1 - 1) - ( k・2a+1- 1) = k ( 3a+1 - 2a+1 )
∴ n2a+2 - n0 = k ( 3a+1 - 2a+1 )
ここで a = 0 は m が奇数を意味する。
(4) 奇数 n0 を 3 倍して 2 で割る処理を 1 回して直ぐに偶数となるような n0 があるとすると
n1 = 3n0 + 1
n2 = n1/2 = (3n0 + 1)/2 が偶数だから
3n0 + 1 = 2ak の形にならねばならない。但し a: 2 以上の整数、k:自然数
k = (3n0 + 1)2-a , n3 = n2/2 = (3n0 + 1)/22
n3 - n0 = (3n0 + 1)/4 - n0 = (3n0 + 1 - 4n0)/4 = (- n0 + 1)/4 < 0
このような n0 = (2ak - 1)/3 は n0 より小さい n3 に帰着する。
一般的には n0 = 4h - 3 の形では
n1 = 3n0 + 1 = 3(4h - 3) + 1 = 12h - 8
n2 = n1/2 = 6h - 4
n3 = n2/2 = 3h - 2
n3 - n0 = 3h - 2 - (4h - 3) = 1 - h ≦ 0 (等号は h = 1 でのみ成り立つ)
h = 1 では n0 = 1 で n3 = 1 、h > 1 では n0 より小さい n3 に帰着する。
これらの n3 は h が偶数のとき偶数となり少なくとももう1回 2 で割れる。
( n0 = 5→4 , 9→7 , 13→10 , 17→13 , 21→16 , 25→19 , 29→22 ,・・・)
これに対し n0 = 4h - 1 = h22 - 1 の形では
n1 = 3n0 + 1 = 3(4h - 1) + 1 = 12h - 2
n2 = n1/2 = 6h - 1 > 0 で n2 が n0 より大きい奇数となる。
(5) 奇数 n0 を 3 倍して 2 で割る処理を m(1) 回して初めて偶数となるような n0 を求める。
n1 = 3n0 + 1
n2 = n1/2 = (3n0 + 1)/2
n3 = 3n2+ 1 =3(3n0 + 1)/2 + 1 = (32n0 + 31 + 21)/2
n4 = n3/2 = (32n0 + 31 + 21)/22
n5 = 3n4 + 1= (33n0 + 32 + 3121)/22 + 1 = (33n0 + 32 + 3121 + 22)/22 = 33n0/22 + (3/2)2 + (3/2)1 + 1
n6 = n5/2 = (33n0 + 32 + 3121 + 22)/23 = (3/2)3n0 + ( (3/2)2 + (3/2)1 + 1)/2
n7 = 3n6 + 1 = (34n0 + 33 + 3221 + 3122 + 23)/23 =3(3/2)3n0 + ((3/2)3 + (3/2)2 + (3/2)1 + 1)
n8 = n7/2 = (34n0 + 33 + 3221 + 3122 + 23)/24 = (3/2)4n0 + ((3/2)3 + (3/2)2 + (3/2)1 + 1)/2
n9 = 3n8 + 1 = (35n0 +34 +3321 + 3222 + 3123 + 24)/24 = 3(3/2)4n0 + (3/2)4 + (3/2)3 + (3/2)2 + (3/2)1+1)
n10 = n9/2 = (35n0 + 34 + 3321 + 3222 +3123 + 24)/25 = (3/2)5n0 + (3/2)4 + (3/2)3 + (3/2)2 + (3/2)1+1)/2
・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
| n2m(1) | = (3m(1)n0 + 3m(1)-1 + 3m(1)-22 + 3m(1)-322 + ・・・ + 322m(1)-3 + 312m(1)-2 + 2m(1)-1)/2m(1)
|
| = (3/2)m(1)n0 + { (3/2)m(1)-1 + (3/2)m(1)-2 + (3/2)m(1)-3 + ・・・ + (3/2)2 + (3/2)1 + 1 }2-1
|
| = (3/2)m(1)n0 + 2-1{ (3/2)m(1) - 1 } /{ (3/2) -1 }
|
| = (3/2)m(1)n0 + 2-1{ (3/2)m(1) - 1 }/(1/2)
|
| = (3/2)m(1)n0 + (3/2)m(1) - 1
|
| = (3/2)m(1)n0 + (3/2)m(1) - (2/2)m(1)
|
| = (3m(1)n0 + 3m(1) - 2m(1))/ 2m(1) = (3/2)m(1)(n0 + 1) - 1
|
n2m(1) = (3/2)m(1)(n0 + 1) - 1 が偶数となる条件は
(n0 + 1) が 2m(1) で割り切れ且つその商が奇数である。
従って k1 を奇数として n0 = k12m(1) - 1 がその条件となる。
ここで m(1) = 1 のときは前項で調べた n0 = 4h - 3 = (h21 - 1)21 - 1 形に相当する。
nm(1) が初めて偶数になるのは n0 = k12m(1) - 1 で k1 が奇数のときだから
k1 = 2h - 1 として n0 = 2m(1)+1h - 2m(1) - 1 の形をとり、
n2m(1) - n0 = 3m(1)k1 - 1 - 2m(1)k1 + 1 = (3m(1) - 2m(1))k1 = (3m(1) - 2m(1))(2h - 1)
n2m(1)が偶数になったとき
n2m(1) = (3/2)m(1)(n0 + 1) - 1= 3m(1)k1 - 1
q1 を奇数 、p(1) ≧ 1 として
n2m(1) = 3m(1)k1 - 1 = q12p(1) となるとき n2m(1) が初めて偶数になるとすると
このとき奇数 k1 は k1 = (q12p(1) + 1)/3m(1)となる。
<例>(n0,p(1),m(1),k1,q1)=(35,4,2,1,5),(155,1,2,39,175),(14563,15,2,3641,1)
| n0 | n1 | n2 | n3 | n4 | n5 | n6 | n7 | n8 | ・・・ | n13 | ・・・ | n19
|
|---|
| 35 | 106 | 53 | 160 | 80 | 40 | 20 | 10 | 5 | ・・・ | 1 | |
|
| 55 | 466 | 233 | 700 | 350 | 175 | 526 | 263 | 790 | ・・・ | 593 | ・・・ | 334
|
| 14563 | 43690 | 21845 | 65536 | 32768 | 16384 | 8192 | 4096 | 2048 | ・・・ | 256 | ・・・ | 1
|
m(1) = 2 , n2m(1) = n4 で赤字、青字は q1
n2m(1) を p(1) 回 2 で割れば n2m(1)+p(1) = q1 なる奇数に達する。
ここで、 q1 = n0 となることがあるかどうかを調べる。
| z1 | = q1 - n0 = (3m(1)k1 - 1)/2p(1) - n0
|
| = {3m(1)(n0 + 1)/2m(1) - 1}/2p(1) - n0
|
| = {3m(1)(n0 + 1)2-p(1)-m(1) - 2-p(1) - n0
|
| = n0(3m(1)2-p(1)-m(1)- 1) + 2-p(1)(3m(1)2-m(1) -1)
|
| = [n0{3m(1)-2p(1)+m(1)} + {3m(1)- 2m(1)}]/2p(1)+m(1)
|
z1 = 0 となるのは
n0 = (3m(1) -2m(1))/(2p(1)+m(1)- 3m(1)) のときであり、
2p(1)+m(1)- 3m(1) が 3m(1)- 2m(1) の約数となりうるのは
m(1) = 1 , p(1) = 1 のときで n0 = 1 となる。即ち n0 = 1 のときは z = 0 となる。
それ以外では n0 は正の整数となり得ないので z = 0 とはならない。
z1 = [n0{3m(1)-2p(1)+m(1)} + {3m(1)- 2m(1)}]/2p(1)+m(1) において
3m(1) - 2m(1) > 0 , 2p(1)+m(1) > 0 で
2p(1)+m(1) - 3m(1) は p(1) の変動により正負が入れ替わる。
z1 の正負の入れ替わり点は 2p(1)+m(1)- 3m(1) = 0 であるが、
2p(1)+m(1) - 3m(1) ≠ 0 (第1項は偶数で、第2項は奇数) であり、z1 = 0 とはならない。
この q1 が 最初の n0 より小さくなるには z1 < 0 とならねばならないので、
n0(3m(1)-2p(1)+m(1)) + 3m(1) - 2m(1) < 0
∴ n0(2p(1)+m(1)- 3m(1)) > (3m(1) - 2m(1))
少なくとも 2p(1)+m(1) > 3m(1) が成り立たねばならない。
∴ 2p(1) > (3/2)m(1)
m(1) = 1 のときは p(1) = 1 で n3 が n0 より小さくなることは前項で調べたとおりである。
上記例において
n0 = 35 のとき m(1) = 2, p(1) = 4, 2p(1) > (3/2)m(1) で q1 = 5 < n0
n0 = 155 のとき m(1) = 2, p(1) = 1, 2p(1) < (3/2)m(1) で q1 = 175 > n0
n0 = 14563 のとき m(1) = 2, p(1) = 15, 2p(1) > (3/2)m(1) で q1 = 1 < n0

 E-mail
E-mail
 戻る
戻る
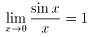
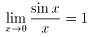 を使って証明される事だから.
を使って証明される事だから.


 E-mail
E-mail
 戻る
戻る