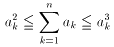
を満たすとき、次の不等式が成り立つことを示せ。
Weekend Mathematics/コロキウム室/NO.157
| NO.1324 | 2002.11.17. | yokodon | ある不等式の証明・その2 |
模試シリーズ14
(1)0 でない2つの実数 a, b が
a ≦ b , a2 ≦ a + b ≦ a3 , b2 ≦ a + b ≦ b3
を満たすとき、a2 + b2 の最小値と最大値を求めよ。
(2)n を2以上の自然数とする。0 でない n 個の実数 ak(k = 1, 2, ..., n)
が、全ての k(k = 1, 2, ..., n)に対して、次の条件:
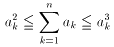
を満たすとき、次の不等式が成り立つことを示せ。
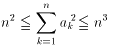
(一部訂正:11/18 23:00)

| NO.1325 | 2002.11.17. | yokodon | 曲線に関する積分 |
模試シリーズ15
曲線C;
x = cos3(t) , y = sin3(t) , 0 ≦ t ≦ π/2
の全長を L 、曲線C上の点PにおけるCの接線と原点との距離を h 、点 (1, 0) と
点Pを結ぶ曲線Cに添った弧長を s とする。ただし、点Pが (1, 0) 又は (0, 1)
に一致するときには、h = 0 とする。このとき、以下の値を計算せよ。
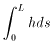

| NO.1326 | 2002.11.18. | Junko | 素数定理(3) |
整数x以下の素数の個数をπ(x)とします。
たとえば、8以下の素数は、{2,3,5,7}の4つですから、π(8)=4です。
次に、π(x)/xを考えます、つまり素数の個数の割合です。
xが増えるに従って、この値は小さくなっていきますが、それには法則性があるのでしょうか?
それに対する答えが、素数定理ということになります。
素数定理
xが大きいとき、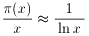
つまり整数の中で素数の出現する割合は、xが大きい数であれば、ln x の逆数に
ほぼ等しいということになります。
こんなところに自然対数が出てくるというのは、不思議というか、妙な感動を覚えますね。
詳しくは、現代数学社から出ている「数学の宇宙」(\3500)という本に出ています。
この本によれば、1896年、ジャック・アダマールとC.j.ドラヴァレ・プサン
によって、解析数論の大変微妙なテクニックを使って証明された、とあります。

| NO.1327 | 2002.11.21. | ニースケンス | 最大・最小となる点(3) |
yokodon さんのNO.1322 最大・最小となる点(2)の
(2)の解答の中に
S0 = 1/2×(3x)・a ... (*)
という式がありますが、
直線APとBCの交点をKとおくと、
(*) ⇔ S0 = 3△PBC
⇔ AK = 3PK
ですから、Pは...

| NO.1328 | 2002.11.21. | 中川 幸一 | 曲線に関する積分(2) |
x=cos3 t
y=sin3 t (0≦t≦π/2) のとき,
dx/dt=-3 cos2 t sin t …(1)
dy/dt=3 sin2 t cos t …(2)
であるから, 0≦t≦π/2 において,
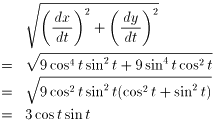
したがって, 0≦t≦π/2 として,
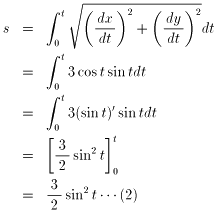
また, 0<t<π/2 のとき, P(cos3 t , sin3 t) における C の接線の傾きは, (1) から,
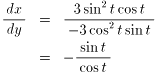
であるから, 接線の方程式は
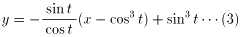
すなわち,
(sin t) x + (cos t) y - cos t sin t =0 …(3)
となる
(3) は,
t=0 のとき, y=0
t=π/2 のとき, x=0
となるから, (3) は 0≦t≦π/2 で成り立つ表現である
よって, 0≦t≦π/2 で,
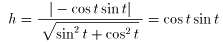
(2) から,
ds/dt =3 cos t sin t
であり, t と s の対応は次のようになる
t:0 → π/2
s:0 → 3/2 (=L)
したがって,
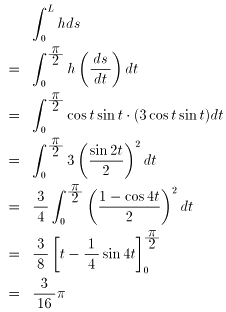
となる

| NO.1329 | 2002.11.23. | 中川 幸一 | 互いに素(10) |
過去の数学の資料を探っていたら面白い問題を見つけたので紹介します。
『でたらめに選んだ2個の正の整数が互いに素となる確率Pを求めよ。』

| NO.1330 | 2002.11.23. | Junko | 互いに素(11) |
以前コロキウム室でも話題になりました。
テーマ別の部屋、互いに素にあります。

| NO.1331 | 2002.11.24. | 水の流れ | 自然数の分割 |
太郎さんは、生徒と一緒に大学入試問題を眺めていたところ、慶應義塾大学に出ていた次のような問題をみつけました。


| NO.1332 | 2002.11.24. | 中川 幸一 | 互いに素(12) |
2つの整数がともに整数kで割り切れる確率は 1/k2 である。
したがって、2つの整数が2でも3でも割り切れない確率は、
1 - 1/22 - 1/32 + 1/62 = (1 - 1/22)(1 - 1/32)
このように考えると、2つの整数が互いに素になる確率、すなわち、どの素数でも割り切れない確率は、
P = (1 - 1/22)(1 - 1/32)(1 - 1/52)(1 - 1/72)(1 - 1/112)…
になることが分かります。無限等比級数の和の公式
1/(1-x) = 1 + x + x2 + x3 +…
を用いて計算すると、
| 1/P | = (1 + 1/22 + 1/24 + 1/26 +…)(1 + 1/32 + 1/34 + 1/36 +…)(1 + 1/52 + 1/54 + 1/56 +…)… |
| =1 + 1/22 + 1/32 + 1/42 + 1/52 +… | |
| =ζ(2) |
この問題はロシアの数学者 P.L.Chebyshev (1821-1894) が考えた ζ(2) に関する面白い問題です。

 E-mail
E-mail
 戻る
戻る