| NO.1488 | 2004.10.1. | DDT | 可換な行列の全体(3) |
可換な行列の全体について、一つの十分条件をみつけたと思います。
yokodonさん,三角定規さんと代数的な方向だったので、幾何学的(?)なアプローチをしてみました。
1.問題の観察
言葉の節約のため、行列Xが行列Aの多項式で表されること、
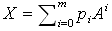
を簡単に、XはAのベキで展開できると表しておきます(piは体の元)。
問題は以下のようなものです。
以下ベクトルをxと書きたいので、行列XはBで代用します。AX=XAのとき、XがAのベキで展開できる条件を求めよ。 (1)
問題(2)の条件、AB=BAからすぐ思いつくのは、 運が良ければAとBは同時対角化可能というものです(例えばAとBが正規行列の場合)。 (2)を一的に解くのは難しそうなので、AとBは同時対角化可能と仮定して、 一般条件へのさぐりを入れてみます。AB=BAのとき、BがAのベキで展開できる条件を求めよ。 (2)
2.問題の適不適
AとBが同時対角化可能なら、AとBは固有ベクトル基底を共有します。
共有される固有ベクトル基底に移った場合、
AとBは対角成分に固有値が並ぶ対角行列に同時対角化されます。それを、
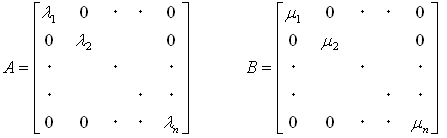 (3)
(3)
とします。ここで(λi)と(μi)はAとBの固有値で、AとBの次数はnです。
もしこのときBがAのベキで展開可能とすると、Aiは、
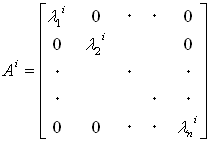 (4)
(4)
なので、
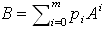
なら、
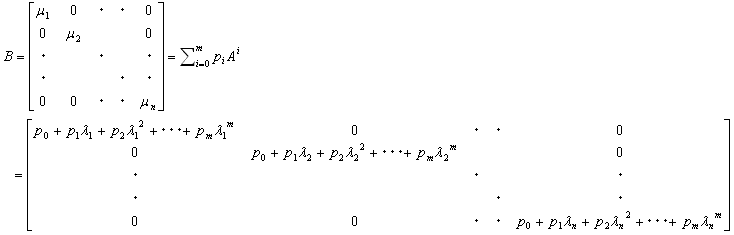 (5)
(5)
となります。(5)の条件をまとめると、
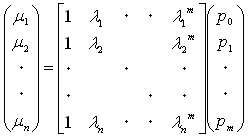 (6)
(6)
が得られます。条件(6)が解 (p0,p1,・・・,pm)t を持てば、
Aと可換なBは、
Aのベキで展開可能となります。ここで上付き " t " は、転置を表します。
(6)が解を持つ条件を探ってみます。
1) m≧n(m>n−1)なら(6)は不定解を持ち、Aと可換なBは明らかにAのベキで展開可能。
2) m<n−1なら、(6)は条件過多となり、 (μ1,μ2,・・・,μn)t の値しだいで、解を持ったり持たなかったりするのは明らか。
3) よって自明でない解を持つ条件は、m=n−1の場合。
以後、条件3)の場合のみ扱います。
3.一つの十分条件
(6)でm=n−1とした場合、(6)の係数行列は
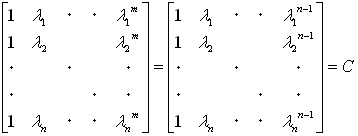
となり、n×n次の正方行列です。よって(6)が解を持つ一つの十分条件は
(BがAのベキで展開できる十分条件は)、
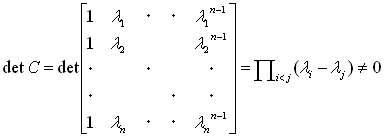 (7)
(7)
となります。(7)は有名なヴァンデルモンドの行列式で、
面倒臭いですが上記にように具体的に計算できます。
従って「AとBを同時対角化可能とした場合」には、
「Aの固有値が全て異なること」は「BがAのベキで展開できる一つの十分条件」です。
が得られます。ところが、Aの固有値が全て異なってAとBが可換なら、 AとBは同時対角化可能です。証明は簡単です。AとBを同時対角化可能として、
Aの固有値は全て異なる ⇒ BがAのベキで展開可 (8)
xiを固有値λi(i=1〜n)に属するAの固有ベクトルとすると、
より、Bxiも固有値λiに属するAの固有ベクトルであることがわかります。 ところがAの固有値は全て異なるので、Aの全ての固有空間Vi(i=1〜n)の次元は1です。 Bxi∈Viなのは明らかなので、Bxi=μixi であることが必要。従って、xiは固有値μiに属するBの固有ベクトル。ABxi=BAxi
ABxi=λiBxi
A(Bxi)=λi(Bxi)
Aの固有ベクトル全体をBase(A),Bの固有ベクトル全体をBase(B)とすると、 これはBase(A)⊂Base(B)を意味するが、Base(A)はもともと固有ベクトル基底なので、 Base(B)の中にBase(A)のベクトルと独立なものは含まれない。 よってBase(A)=Base(B)とでき、AとBは固有基底を共有する。
従って、次が得られました。
となり、「Aの固有値が全て異なる」は一つの十分条件です。行列AとBの次数をnとする。
Aの固有値が全て異なる ⇒ AB=BAとなるBは、Aの(n−1)次のベキで展開可能 (9)
4.一般の場合
Aの固有値が全て異なるときには、Aと可換なBは、Aと固有基底を共有しますが、
Aの全ての固有値とBの全ての固有値が一致するとは限りません。実際二つの対角行列
diagA(λi)とdiagB(μi)を勝手にもってきて、
diagAがAに対応するとして(λi)が全て異なるとしても、
diagBは重複固有値を持てます。これらに任意の相似変換をかけて得られる行列AとBは、
(9)の条件を全て満たすので、こういう事は実際にあり得ます。
この状況は、
と表現できます(直和なのは、異なる固有値に属する固有空間は独立な不変部分空間だから)。 ふつう固有空間は次元1に限定して定義され、(10)に現れるような不変部分空間は、 高さ1の根ベクトル(固有ベクトル)からなる根空間と呼ばれるのかもしれませんが、 ここでは簡単に固有空間と呼んでおきます(じつは正式な用語法を知りません。 根空間については、すぐ後に定義します)。Bの固有空間は、Aの固有空間の直和である (10)
(10)の状況を一般化すると、
が得られそうです。ここで固有値λiに属するAの根空間とは、行列Aの特性多項式を、Bの根空間は、Aの根空間の直和である (11)
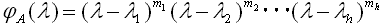
とした場合、
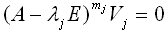 (12)
(12)
で定義されるAの不変部分空間Vjのことで、mjは固有値λjの重複度を表し、
m1+m2+・・・+mh=nです。また、x∈Vjのことを、固有値λjに属するAの根ベクトルと定義します。
さらに根空間Vjは、互いに素な行列多項式 (A−λj)mj(j=1〜h)の核空間でもあるので、
全空間をVnとしたとき、
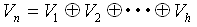 (13)
(13)
も成立ちます。ここで ○ つきの + は、直和を表します。よって(Vj)は
互いに独立な不変部分空間です。個々の根空間の任意の基底を集めてつくったVnの基底を、
根ベクトル基底と呼んでおきます。
いまBが、Aの(n−1)次のベキで展開可能とします。例えばAの根ベクトル基底に移ったとき、
根空間は互いに独立な不変部分空間なので、Aは、
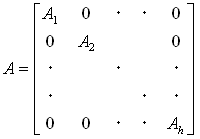 (14)
(14)
の形になります。ここで各Ajは、固有値λjに対応する正方対角ブロックで、
その次数はmjです。
さらにAの根ベクトル基底として、Jordan基底を選んだとします。
各Ajは、JordanブロックJk(j)を用いて、
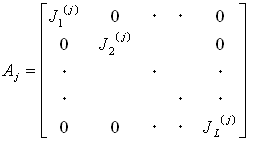 (15)
(15)
と分解されます。各JordanブロックJk(j)は、次の形をしています。
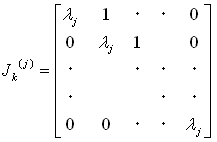 (16)
(16)
(Jk(j))iは、次の形をしています(簡単な手計算でいけます)。
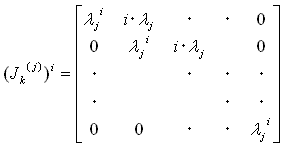 (17)
(17)
(ただしi=0のとき、i・λjの部分は1になる)
(14)〜(17)を見渡し、
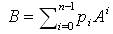
に注意すると、
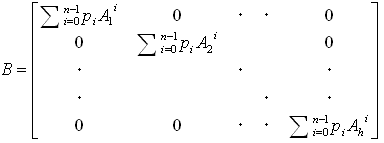 (18)
(18)
であり、Bの対角ブロックΣi=0〜n-1 piAji は、
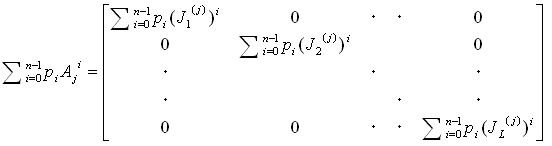 (19)
(19)
となります。最終的にBは、
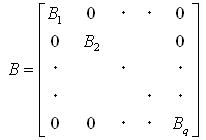 (20)
(20)
の形を持たなければならず、各Brは、
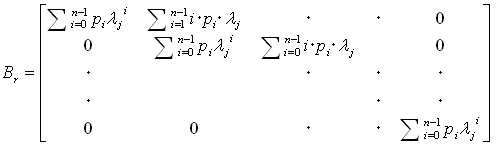 (21)
(21)
(ただしi=1のとき、i・pi・λjの部分はp1になる)
という形をしています。これはBとAが、定数倍の違いを除いてJordan基底を共有することを意味します。
このとき(6)と同様な議論を行って、(p0,p1,・・・,pn-1)tが存在することを要求すると、
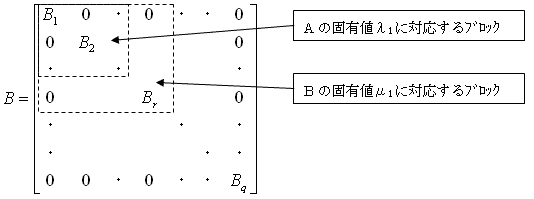
という状態が要求されます。従って、
が成り立ちます(ただし不定解も許します)。またこのときAとBが可換なのは明らかと思えます。Bの根空間は、Aの根空間の直和である (22)
以上まとめれば、
が成り立つように思えます。(23)の右辺に対して、「Aの固有値は全て異なる」のよう な簡単な判定条件をみつけられたら、解答になると考えます。AB=BAとなるBは、Aの(n−1)次のベキで展開可能 ⇔ Bの根空間は、Aの根空間の直和 (23)
[参考文献]
・線形代数(行列とその標準形),伊理正夫・韓大舜,シリーズ新しい応用の数学16,1977年,教育出版.
(この本は古い本ですが、いまだに日本における線形代数の標準的テキストと思えます。
実際いまでもこのシリーズは全巻入手可能です)

| NO.1489 | 2004.10.2. | BossF | 3本のくじ(2) |
一部修正(10/3)
[問題1]
n個の数から重複を許して3個選ぶのに対応
nH3=n+2C3 通り…答
[問題2]
n個の数から異なる3個選ぶのに対応
nC3 通り…答
[問題3]
2〜n-1 の n-2個の数から異なる3個(小、中、大)を選び
小−1、中、大+1なる3数を作れば、これが、題意の場合に対応するから
n-2C3 通り…答
[問題4]
3と同様に 3〜n-2 の n-4個の数から異なる3個を選べばいいから
n-4C3 通り…答

| NO.1490 | 2004.10.3. | Junko | 3本のくじ(3) |
問題1
重複順列と考えて、n3? と答えてしまいましたが、
よくよく考えてみれば、NO.1489 BossFさんのおっしゃる通り、
重複組み合わせですね。
問題2
こちらは一端引いたくじは元に戻さないと考えて、
nC3=n(n-1)(n-2)/6
問題3
n-2C3=(n-2)(n-3)(n-4)/6
問題4
n-4C3=(n-4)(n-5)(n-6)/6

| NO.1491 | 2004.10.3. | DDT | 超ハード数学SF? |
1.事の起こり
いまにして思えば事の起こりは、
Card(N)=Card(Q)<Card(R) (1)
を知った時でした。ここでNは自然数全体,Qは有理数全体,Rは実数全体を表し、Card(*)はその基数です。
(1)はCard(N)<Card(R)を導くので、これは自然数全体を使用しても、実数全体は数え尽くせないことを意味します。またCard(N)=Card(Q)より、実数全体の中で無理数全体は、有理数全体より、さらに圧倒的無限であることをも意味します。
ちなみにCard(N)=Card(Q)に関しては、Nと任意集合Aとの間の双射付け(1対1かつ上への写像)が数えること(番号付)の定義(抽象化)なのだと、かなり強引に自分を納得させましたが、Card(Q)<Card(R)については、そこに現れる対角線論法に途轍も無い異様さを感じて、馴染むのに2年ほどかかりました。その間に私は、数値計算(有限要素法や境界要素法)をけっこうやるようになりました。つきつめるとこれらは、連続関数の近似問題になります。そして2年ほどたったある日、次のことに気づきました。
2.連続関数の近似問題と選点法
話を連続関数の近似問題に限ります。実用上、有限個の区間で区分的に連続な関数は、有限個の区間に区分して考えれば区間内で連続関数ですし、いかにも不連続そうな観測データなどを扱っていても、観測値を折れ線でつないでしまえば、ぎざぎざな連続関数として扱うことができます。もちろん連続関数であることを保証する理屈があるに越したことはありませんが、理屈の上ではいたるところ不連続な関数であっても、実用的にはふつう、そのぎざぎざ連続近似を扱うと思います。選点法とは、以下のような連続関数の近似法です。
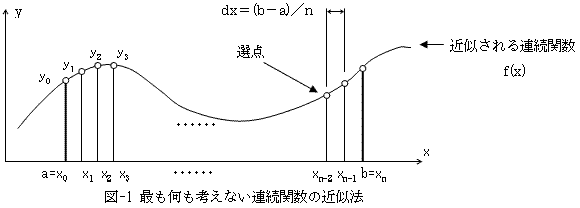
図-1のように、近似される連続関数の定義域が[a,b]だった場合、区間[a,b]をn等分して分割幅を、
dx=(b−a)/n
と定めます。xi=a+i・dxにおいて関数値yiを計算して、次の選点Siを定義します。
Si=(xi,yi) (2)
(2)のyiは、解関数である連続関数f(x)を定める微分方程式や偏微分方程式を満たすように、またはf(x)が観測データであれば、xiにおける観測値yiに等しいようにとられます。xiとxi+1の間は、例えば直線で補間します。これを選点法といいます。要するに選点法とは、選ばれたサンプル点(xi,yi)では、解関数に等しい正しい関数値yi=f(xi)を必ず与え、その間では近似の度合いに応じて解関数との誤差が生じるという方法です。
連続関数の近似法はごまんとありますが、基本的な発想は全て選点法と同じです。つまり選点法は、連続関数の近似法の基礎となる考え方ですが、選点法によって正しい解関数に到達できるという保証はあるのでしょうか?。あたりまえの答えは、
定義域のn等分割を無限に細かくすれば良い. (3)
というものです。どうしてかというと、
定義域のn等分割を無限に細かくすれば、いつかは定義域の全ての点を尽くせるから. (4)
です。つまりdx → 0に追い込むことによって無限に増えた選点Siは、解関数上の全ての点をいつかは覆い尽くすので、xiとxi+1の間の補間は必要なくなるというものです。選点Siとは、yiが必ず解関数に等しい正しい関数値を与える点のことでした。(1)のCard(N)=Card(Q)<Card(R)を知っていらい2年間、これは当然のことと思っていました。本当にそうでしょうか?。
3.本当にそうなの?
例えば2.の解関数である連続関数f(x)の定義域[a,b]を、[a,b]=[0,1]だとします。あたりまえの答えに従えば、実数区間[a,b]=[0,1]をn等分割するnを無限に大きくしていけば、いつかは実数区間[0,1]上の全ての点を尽くせると言ってるのと同じです。しかもnは自然数です。そういうことは不可能と言ったのがカントルの対角線論法のはずです。実際nを自然数として区間[0,1]を無限に細かくn等分割して得られる点とは、[0,1]内の有理数全体です。整数のペアの同値類を有理数とみなすとかいったのではない、初等的な有理数の構成法を考えれば、これは明らかと思えます。よって、Card(N)=Card(Q)<Card(R)なので、区間[0,1]内の全ての有理数を尽くせたとしても、それより無限に多くある無理数点では、選点法は正しい結果を与えきれないはずです。イメージを描くと、以下のようになります。
得意の(?)可算無限顕微鏡を持ち出します。まず可算無限高倍率の顕微鏡は、有理数の並びをバラバラに離散化できるだけの性能を持ちます。どうしてかというと、Card(N)=Card(Q)より、有理数は自然数で番号付け可能だからです。この仮定のもとに、図-1の可算無限極限、すなわちn→∞での選点法近似の状態を、可算無限顕微鏡で覗いたとします。結果は次の図-2になると思えます。
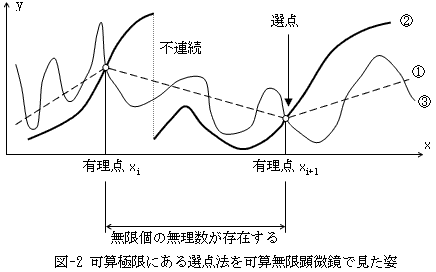
図-2において、選点法の分割は可算無限に細かいので、選点は隣り合った有理点xi,xi+1上にあるとします。点線①が選点法により予想される解です。選点法は、選点上では正しい関数値を持つという方法でした。従って有理数だけで実数全体を尽くせるなら、①が正解であり、①は近似解ではありません。ところがCard(N)=Card(Q)<Card(R)であるために、選点は隣り合った有理点xi,xi+1上にあるにも関わらず、xiとxi+1の間には無限に多くの無理数点が存在し、太実線②のように本当の解は不連続かもしれません。連続な解に限ったとしても、実線③のように点線①と一致するとは限りません。
人間に正確な数値計算は可能なのでしょうか?。選点法の発想は正しいのでしょうか?。もっと一般的に、任意の数値計算の基礎が選点法と同じであるならば、数値計算は可能なのでしょうか?。
もちろん連続無限個(Cared(R)個)の選点を発生できれば、話は別なのですが、
NO.1476やNO.1485で述べたように、可算無限には「人間が構成的に作り出せる最大無限」という裏の意味があります。現行理論を信じる限り実数全体には、どのような数値計算手法を用いても決して到達できません。たとえその数値計算手法に、可算無限回の操作を許したとしても駄目です。
4.等式延長の原理
以上の結論は、数値計算を日常的に実行する私にとって受け入れ難いものでした(やってられないじゃないですか)。一度「人間って本当に連続関数を近似出来るんですか?」と、それとなく教授にきいてみたことがあるのですが、「なに訳わからんこと言ってるんだ!」と、はっ倒されました(気持ちはわかります)。それからしばらくして、次の定理を見つけました。
等式延長の原理 |
証明は以外に簡単です。
1) [分離公理]より、Y×Yの対角集合は閉集合。
2) f(x)=g(x)となるx∈Xの全体をBとする。⊿={(f(x),g(x))|x∈B} は Y×Yの対角集合で閉。
3) fとgがXで連続だから、写像h:B → ⊿ は連続。
4) 定義より、A⊂ h-1(⊿)は明らか。
5) A⊂ h-1(⊿)は、2)と3)よりXの閉集合(連続写像の一般的性質)。
6) 
7) 従ってYを分離空間として、Xで連続なfとg:X → Y が、Xで密なA上でf=gなら、Xでf=g。
(証明終わり)
8) とはいえ一般位相論の本をベタに読むと、[分離公理]を読み出す前に、かなりの息切れ状態になっているはずです。
ふつうの言葉で言うと、実数直線Rは分離位相空間であり当然任意の位相空間の条件を満たします。またXの密集合Aとは、X=Rの場合A=Q⊂R=Xとできます。従って、
等式延長の原理‘ |
選点法が正解へ収束することは、等式延長の原理が保証してくれます。
解関数の定義域Iをどんどん細かく分割し、定義域上にできるだけ細かく一様に選点をばらまくとは、
「等式延長の原理‘」において、定義域Iの有理数全体A上で、関数gをシミュレートすることに当たります。
関数gを解関数fの候補とすれば、当然定義域全体Iでgは連続とみなされます。この話の最初の仮定より、もちろん目的の解関数fはIで連続です。Iに含まれる有理数全体A上で、Iで連続なgが定義されてしまえば、A上でgに一致してIで連続な解関数fは、「等式延長の原理‘」よりA上でf=gなので、I上でもf=gとなり、選点法の収束結果の一意性がI上で保証されます。
従って、本来は連続無限個の点での関数値を定めなければならない連続関数の近似問題を、可算無限個の点での関数のシミュレーション問題におきかえることができます。「等式延長の原理」は、数値計算が可能になる基本原理ではないのかと、個人的には思っています。
5.数学はハードSF?
全ての近似計算は、知らず知らずのうちに2段階のシミュレーションをやっています。それを表したのが図-3です。図-3の此岸の世界に、ほとんど張り付くような点線が実際の数値計算で行える範囲です。可算無限は理屈の上では可算極限で到達できますが、ほんとうにそんな事ができる人は一人もいないので、真実は彼岸の彼方の世界です。此岸の数値計算は、彼岸の中間生成物を近似するにすぎず、超彼岸にある正解には到達できません。そこで此岸から彼岸へのシミュレーションが、彼岸から超彼岸へのシミュレーションと同等であるお墨付きを、「等式延長の原理」から貰うわけです。
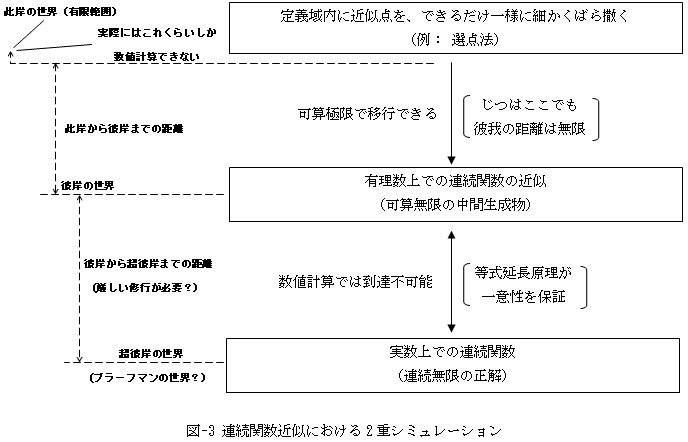
図-3の此岸,彼岸,超彼岸(ブラーフマン?)は冗談で書きましたが、こんな階層を考えついたカントルの想像力には本当に厳しい修行が必要だったと、その人物伝には書いてあります(無限集合論を考え出したために、精神病になりました)。
ところで世界中の誰一人として、此岸の世界以外は見たことがありません。それは図-3において、ほんのちょっとの部分です。残り全ての無限については、誰一人としてその正しさを確認できません。単純な連続関数の近似問題一つとってみても、広大な未確認領域が必要であり、数値計算で確認可能なのは氷山の一角というのが実数論の現状です。しかもこの一角は、対する未確認領域が無限なので、実質0に等しい小ささです。このあたりの事情もさして森毅は、「実数は数学的には正当だが、都合の良いフィクションだ」と言ったのだと思います。でも数学って、素のままでけっこうハードSFじゃないですか?
6.超ハード数学SF?
以下与太話です。が、白状するとじつはこれを書きたくて、
NO.1476もNO.1485も書いたようなものです。
これから量子だの時空だの、カッコつけて小難しいことを言い出しますが、本人もほとんどわかっておりません。
量子力学の正しさを確認する実験において、実験結果と計算結果が、小数以下30桁とか300桁とかの精度で一致したなどという話をよく聞きます。最先端の理論物理学の実験なので、外乱をできるだけ排除するために、反応部を絶対零度に冷却したりして、恐ろしく高精度な実験なのはわかりますが、「でもこれってやっぱりちょっと合いすぎではっ?」と思ったことはないですか?。だっていくら等式延長の原理により、可算無限近似の有限シミュレーションが連続無限の正解と同等といったって、有限はしょせん有限です。有限的にいくら細かく関数を近似したところで、図-2の①と③のような状態にどうしてならのかが不思議です。いったいどこまで細かく近似すれば十分なのか?。一般論としては、図-3の状態から考えて相手は無限なので、いくら細かく近似しても図-2の①と③の状態は不可避です。それを30桁の精度で一致したなどとは、とても信じられません。これが10-30 mのことなら、「その精度はそこいらの原子の原子半径より小さなことになる」とは、やっぱり森毅の言葉です。
私は答えを見つけた(嘘です。もちろん)。
数学は全ての物理計算の基本だ。現実の世界を扱う物理の数値計算において、それが実験値とぴったり合うからには、こうだ!。
時空間は統一場理論が言うように、量子効果により離散化されている!
つまり、等式延長の原理は不要だ!
例えば距離や時間に最小単位があれば、全宇宙には有限個の距離や時間の粒々しかないから、有限個の実数を扱えば良いことになる。そうすれば全宇宙は、図-3の此岸の世界に収まるから、当然有限近似で連続関数は完璧に再現できる。それを連続な時空間などと仮定するものだから、標準量子力学では観測理論に、確率波波束収束などという無理な考えが登場するわけだ。
これが30桁の精度の秘密だ!。だって図-3で有限の此岸は、あんなに小さいんだもの。だいたい30桁なんてその辺の家庭用PCでひょひょい計算できちゃう桁数だぞ!。宇宙の秘密が家庭用PCで計算できるんだから、絶対そうだ!
(ちなみに家庭用PCの一般CPUのレジスターは多くて20桁なので、多倍長の特別プログラムが必要です)
きけば人間の脳細胞の数は、全宇宙の原子の数より多いそうじゃないか?。時空が離散化されればその数も、宇宙の原子の数とどっこいどっこいだろう(どうせ有限なんだから)。せいぜい1?の容積の脳細胞や、そっから生まれた家庭用PCで太刀打ちできるのも、それで納得できる。だって宇宙全体の原子の数は、1?の脳細胞の数より少ないんだぞ!。(・・・っておいおい理屈んなってないぞ、お前・・・)
本当にこうであれば、血沸き肉踊って深酒して寝てしまうところです。ですが逆の場合はどうでしょう?。
つまり、
せいぜいアインシュタインのブラックホールの特異点が局所的に病的なだけで、
全体的にはおしなべて、美しく単純なニュートンの連続宇宙だった.
こうなります。
トンネル効果とは、絶対に通過不可能なポテンシャルの壁の向うに、なぜか電子が飛び出してしまうというもので、巨視的な世界で言えば、脱出速度に達していないペットボトルロケットが、太陽系外へ逃走してしまうような現象です。これは代表的な量子効果の一つで、江崎レオナはこの効果を利用したトンネルダイオードでノーベル賞を取りました。ニュートン宇宙では、こういうことが一切なくなります。
まず、知らず知らずのうちに量子効果を大々的に採用していた電子機器の大部分は大打撃を受けます。電子レンジは駄目だし、パソコンももちろん駄目、もしかするとラジカセもないかもしれません。そうすると当然ウォークマンもDVDもお釈迦となって、トリニトロンで一躍世界一になったSONYもありませんし液晶もありません。ところが・・・。
有限近似の精度では、連続無限にはとても太刀打ちできなかった。
「等式延長の原理」は有名無実となり、
位置の測定さえもままならない。
今日の首都高予想なるものが出現する。
「荒井ユミで有名な中央フリーウェイは、明日はサザンで有名な茅ヶ崎方面に出現する模様です」
「出現確率は50%。遅刻の用意をお願いします」
「なお滑走路のようなこの道の、右には競馬場も見えません」
擬似量子効果がマクロな世界に結局出現するかもしれません(ほんとか?)。じつはこういう考えには正当な起源があって、これを「量子力学の隠れたパラメータ理論」といいます(ただしマクロな世界には出現しません)。その大御所はデイヴィット・ボームという人で、量子力学に反対したアインシュタインの考えを受け継ぎ、コペンハーゲン学派の量子論の確率解釈に対抗しました。この人は世界的にも有名な物理学者でしたが、隠れたパラメータ理論はその後、鳴かず飛ばずだったと記憶しています。でも話のネタとしては、こっちのほうが面白そうです。
「どうでしょう? 長沼伸一郎さん、ルディー・ラッカーさん」
「この超ハード数学SFネタを買ってくれませんか?」
[参考人物および参考文献]
・長沼伸一郎:
著書「物理数学の直観的方法」や「一般相対性理論の直観的方法」(1990年,1992年。通商産業研究社)で、一躍理工系学生のみならず物理専攻の学生にも大人気となった人物。早稲田大学理工学部応用物理学科(数理物理)卒業後、同大学院中退。「一般相対性理論の直観的方法」の第4章「時空構造への波動論的アプローチ」では隠れたパラメータ理論を展開、量子力学を視覚化しようと試みる。日本ではこの手の話題の数少ない研究者の一人(と思える)。
・ルディー・ラッカー:
いわずと知れた(?)超数学ハードSF作家で現役の数学者(無限基数)。ゲーデルとの対話が余りにも嬉しかったために書いたと思われる「無限と心」(1986年現代数学社)やそのエンタテイメント版であるSF小説「ホワイトライト」(ハヤカワ書房)で有名(?)。他に遺伝的アルゴリズムを扱ったSF小説「ウェットウェア」シリーズがある(ハヤカワ書房)。
・現代物理学における因果性と偶然性,D.ボーム,1969年,東京図書
隠れたパラメータ理論の古典です。
・特集 波動関数のミステリー,数理科学2002年7月号,サイエンス社
現在の量子論の観測理論,確率解釈の最先端に触れることができます。もしかすると、トンネル効果の仕組みも後一歩かも。
(言い訳: 3年ぶりに超ハードな仕事から一瞬だけ解放されて、超ハイテンションでした。)

| NO.1492 | 2004.10.10. | 水の流れ | 三角関数と数列 |


| NO.1493 | 2004.10.18. | ジスルフィド結合 | 素数の存在(1) |
「自然数nと2nの間には少なくとも1つの素数が存在することを示せ。」
をずっと考えているんですが、ずっと分からず、解答をさがしても見つかりません。
帰納法の流れなんかな?と思ってるんですが、
いかんせん「素数」なるものの立式はかなりやりづらく、
素数が存在しないと仮定して、矛盾を導くのかなと思ってもうまくいきません。
非常にあつかましいのですが、解答が分かるのであれば教えていただけないでしょう
か?

| NO.1494 | 2004.10.28. | 加賀 | 素数の存在(1) |
コロキウム室NO.1493のジスルフィド結合さんの質問への返事を書きます。
お尋ねの命題は、「チェビシェフの定理」あるいは「ベルトランの仮説」
として知られているものです。
チェビシェフの定理といっても複数あるので、検索されるのなら、
「素数」などをキーワードに加えたほうが良いでしょう。
書籍なら、例えば「天書の証明」(シュプリンガー)に、
エルデシュによる証明があります。

 E-mail
E-mail
 戻る
戻る