| NO.1495 | 2004.11.1. | 水の流れ | 高次の因数分解(1) |
高次の因数分解を問題にします。次の式を因数分解しなさい。
問題1:x15−1
問題2:x15+1
問題3:x21−1
問題4:x35―1

| NO.1496 | 2004.11.5. | Junko | 高次の因数分解(2) |
問題1:
x15-1の因数分解ですが、(x5)3-13とおけることから、
x15-1=(x5-1)(x10+x5+1)
=(x-1)(x4+x3+x2+x+1)(x10+x5+1)
と因数分解ができます。一方、x15-1は、(x3)5-15とおくこともできますから、
x15-1=(x3-1){(x3)4+(x3)3+(x3)2+x3+1}
=(x3-1)(x12+x9+x6+x3+1)
=(x-1)(x2+x+1)(x12+x9+x6+x3+1)
両者を見比べると、x2+x+1が、x4+x3+x2+x+1 または、 x10+x5+1 を割り切ることがわかります。実際に計算をしてみると、
x10+x5+1=(x2+x+1)(x8-x7+x5-x4+x3-x+1)
であることがわかります。従って、以下のように因数分解できることになります。
x15-1=(x-1)(x2+x+1)(x4+x3+x2+x+1)
(x8-x7+x5-x4+x3-x+1)

| NO.1497 | 2004.11.8. | UnderBird | 高次の因数分解(3) |
x15-1=(x-1)(x2+x+1)(x4+x3+x2+x+1)
(x8-x7+x5-x4+x3-x+1)
私も同様に考えましたが、
(x4+x3+x2+x+1)や
(x8-x7+x5-x4+x3-x+1)が
もうこれ以上整数の範囲で因数分解できないことは、示していません。
実際コンピュータで求めるとその通りですが、これらの多項式が既約であることの
チェックはどうしたらよいか
悩んでます。
因みに、(x4+x3+x2+x+1)の因数分解の場合、
1次との因数分解の可能性については、因数定理より判断できますが、
2次の場合の因数があるかは一々、(x2+Ax+B)(x2+Cx+D)と置くのも、これ以上高次
の場合には一般性に欠けますよね。

| NO.1498 | 2004.11.8. | Junko | 高次の因数分解(4) |
実は私も同じことを考えていました。
実数の範囲(整数の範囲?)を前提にすると、もうこれ以上因数分解できないということを示さないと
いけませんよね。
複素数の範囲で考えれば、方程式x15-1=0の解は、1の15乗根ですから、複素平面上において、
単位円を15等分した点で表わされることになります。
z=cosθ+i sinθ (ただし、θ=2kπ/15 k=0,1,2・・・14)
このことから実数解は「1」だけだということもわかります。
従って、1次の因数は(x-1)だけだということになります。それでも例えば、(x4+x3+x2+x+1)が
2次と2次に因数分解できるという可能性を否定できませんね。
ところで、15個ある方程式x15-1=0の解は、kの値によって、
以下のように分類できます。
- そのままで実数
k=0のとき、1通り
- 3乗してはじめて実数
k=5,10のとき、2通り
- 5乗してはじめて実数
k=3,6,9,12のとき、4通り
- 15乗してはじめて実数
k=1,2,4,7,8,11,13,14のとき、8通り
これが、因数分解の次数と一致しています。偶然ではないですよね?

| NO.1499 | 2004.11.23. | 水の流れ | 自然数の和(1) |
<今回は、2002年の大阪教育大学の入試問題です。>
自然数nをそれより小さい自然数の和として表すことを考える。
ただし、1+2+1と1+1+2のように和の順序が異なるものは別の表し方とする。
例えば、自然数2は1+1の1通りの表し方ができ、
自然数3は、2+1,1+2,1+1+1の3通りの表し方ができる。
問題1:自然数4の表し方は何通りあるか。
問題2:自然数5の表し方は何通りあるか。
問題3:2以上の自然数nの表し方は何通りあるか。

| NO.1500 | 2004.11.26. | yokodon | 高次の因数分解(5) |
ちょっと気になる記載(NO.1496 〜 1498)に対する、
大きなお世話です。
代数学の基本定理によれば、全ての実数係数の多項式は複素数の範囲で1次式の積
に因数分解されることが知られており、且つ n 次多項式が m 個の実数根と q 個の
虚数根(→、ここに「虚数」とは、虚数部分が0でない複素数の意味にご理解下さい
)を持つとき、q は偶数で q = 2p と置けて(つまり、p 組の共役複素数が根にな
る)、m + 2p = n となることもすぐ分かります。
この事を使うと、No.1495 の問1は、実数係数の範囲で以下のように因数分解でき
るはずです。

但し、θk = 2kπ/15, k = 1, 2,..., 7
ここに、
zk = cos(θk) + i・sin(θk) , k = 1, 2,..., 15
と置くと、k = 1, 2,..., 7 に対して、
z15-k = (zk)*
(ここに、複素数 z に対して、その共役複素数を z*で表すことにさせて下さい)
であることを用いました。このことから、例えば z1 と z15 を解に持つ2次方程
式として、
x2 - cos(θ1)・x + 1 = 0
・・・を考えることが出来ます。他も同様です。
このことは、整数係数の範囲での因数分解の「限度」を考える上で、参考になると
思います(現在は、そこまで考える元気がありませんw)。
一般に、「因数分解せよ」という問題は、以上の意味で「どこまで因数分解するこ
とを求められているのか」に関して、ちょっと悩みますよね。f(^^;

| NO.1501 | 2004.11.27. | yokodon | 互いに素な数の列 |
数列 {an}, {bn} を以下で定める。
a1 = 1, a2 = 3, an+2 = 4・an+1 - an
b1 = 1, b2 = 5, bn+2 = 4・bn+1 - bn
(n = 1, 2, 3,...)
(1)
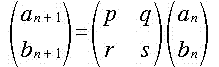
が、n = 1, 2 で成り立つような2次正方行列 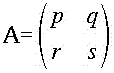 を求めよ。
を求めよ。
また、この時 (*) が任意の自然数 n で成り立つことを示せ。
(2)任意の自然数 n に対して、an と bn は共通な素数の約数を持たないことを
示せ。

 E-mail
E-mail
 戻る
戻る