NO.1643 自然数の分割(2) 2007.1.15. 夜ふかしのつらいおじさん
問題1
Q(1)= 1 (1)
Q(2)= 2 (2,
1+1)
Q(3)= 4 (3,
1+2,2+1,
1+1+1)
Q(4)= 8 (4,
1+3,3+1, 2+2,
1+1+2,1+2+1,2+1+1,
1+1+1+1)
Q(5)=16 (5,
1+4,4+1, 2+3,3+2,
1+1+3,1+3+1,3+1+1, 1+2+2,2+1+2,2+2+1,
1+1+1+2,1+1+2+1,1+2+1+1,2+1+1+1,
1+1+1+1+1)
Q(6)=32 (6,
1+5,5+1, 2+4,4+2, 3+3,
1+1+4,1+4+1,4+1+1, 1+2+3,1+3+2,2+1+3,2+3+1,3+1+2,3+2+1, 2+2+2,
1+1+1+3,1+1+3+1,1+3+1+1,3+1+1+1, 1+1+2+2,1+2+1+2,1+2+2+1,2+1+1+2,2+1+2+1,2+2+1+1,
1+1+1+1+2,1+1+1+2+1,1+1+2+1+1,1+2+1+1+1,2+1+1+1+1,
1+1+1+1+1+1)
より、Q(n)=２n-1と考えられます。これは、次のような操作を考えると納得できます。 例えば、n=4 のとき、{1+1+1+1} から 1番目と3番目の ｢+｣ を取ります。
すると、{11+11} となりますが、これを、{2+2}と書き換えます。
このように、3つある ｢+｣ の取り方をすべて考えます。
3つとも取ると、{1111}→{4}、より1つ（3Ｃ3）。
2つ取ると、{111+1}→{3+1}、{11+11}→{2+2}、{1+111}→{1+3}、より3つ（3Ｃ2）。
1つ取ると、{11+1+1}→{2+1+1}、{1+11+1}→{1+2+1}、{1+1+11}→{1+1+2}、より3つ（3Ｃ1）。
1つも取らないと、{1+1+1+1}、より1つ（3Ｃ0）。
の合計8つ（3Ｃ3+3Ｃ2+3Ｃ1 +3Ｃ0=２3）。
（nＣr は、異なるn個 のものの中からr個組み合わせる場合の数を表します）
問題２
オイラーの5角数定理というのは知らないので与えられた漸化式は使わないことにします。
Ｐ( 1)= 1, Ｐ( 2)= 2, Ｐ( 3)= 3, Ｐ( 4)= 5, Ｐ( 5)= 7,
Ｐ( 6)= 11, Ｐ( 7)= 15, Ｐ( 8)= 22, Ｐ( 9)= 30, Ｐ(10)= 42,
Ｐ(11)= 56, Ｐ(12)= 77, Ｐ(13)=101, Ｐ(14)=135, Ｐ(15)=176,
Ｐ(16)=231, Ｐ(17)=297, Ｐ(18)=385, Ｐ(19)=490, Ｐ(20)=627
となるようです。
n=8まで具体的に求めるようになっていますが、n=6までにします。
P(1)= 1 (1)
P(2)= 2 (2, 1+1)
P(3)= 3 (3, 1+2, 1+1+1)
P(4)= 5 (4, 1+3,2+2, 1+1+2, 1+1+1+1)
P(5)= 7 (5, 1+4,2+3, 1+1+3,1+2+2, 1+1+1+2, 1+1+1+1+1)
P(6)=11 (6, 1+5,2+4,3+3, 1+1+4,1+2+3,2+2+2, 1+1+1+3,1+1+2+2, 1+1+1+1+2, 1+1+1+1+1+1)
例えば、P(4)= 5ですが、数が１つのものは{4}、2つのものは{1+3,2+2}、3つのものは{1+1+2}、4つのもは{1+1+1+1}
ここでｐｋ(n)は、nをｋ個の自然数の和で表した場合の個数とします。
4を2つの自然数の和で表すと、｢1+3｣,｢2+2｣なので、ｐ2(4)=2となります。
P(4)=p1(4)+p2(4)+p3(4)+p4(4)=1+2+1+1=5です。
いくつか大切な式をあげてみます。
P(n)=p1(n)+p2(n)+p3(n)+・・・+pn(n) ･･･ （あ）
pk(n)=p1(n-k)+p2(n-k)+p3(n-k)+･･･+pk(n-k) (ただし、k≦n-k) ･･･ （い）
（い）について、例えば、
p2(5)=p1(3)+p2(3)
p3(5)=p1(2)+p2(2)
pn(n)=1
pn-1(n)=1 （ただし、n≧2）
pn-2(n)=2 （ただし、n≧4）
pn-3(n)=3 （ただし、n≧6）
pn-4(n)=5 （ただし、n≧8）
pn-5(n)=7 （ただし、n≧10）
･･･
つまり、
pn-k(n)=P(k) （ただし、n≧2k） ･･･ （う）
p1(n)=1 ･･･ （え）
（あ）の式の説明は省略します。
（い）の式は次のような意味です。
例えば、p2(5)=2は、{1+4, 2+3}の個数です。
どれも0ではないので、初めに1を与えます。
次に残りの5-2=3の割り振りを考えると、1つだけに割り振る場合、2つに割り振る場合があります。
p3(5)=2は、{1+1+3, 1+2+2}の個数です。
初めに1を与えます。
次に残りの5-3=2の割り振りを考えると、1つだけに割り振る場合、2つに割り振る場合があります。
この場合は、2しか残ってないので2つまでしか割り振れません。
（う）の次の2つは分かりやすいと思います。
pn(n)=1は自明です。
pn-1(n)=1（ただし、n≧2）は（い）から直ちに導けます。
（お）も自明です。
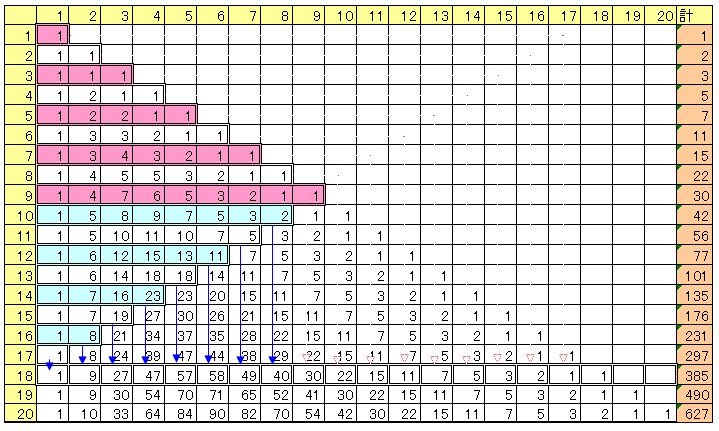
ここで次のようなpk(n)の表を作ります。
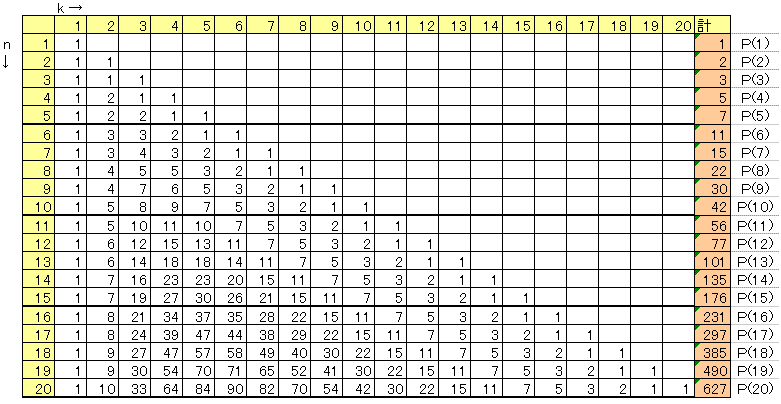
これは、次のように作ります。
黄色い部分は、上で（う）の2つと（え）より1で埋まります。
2列目の数は、2行上の1列目と2列目の数の和です。
斜めの2はすべて2行目の和になります。
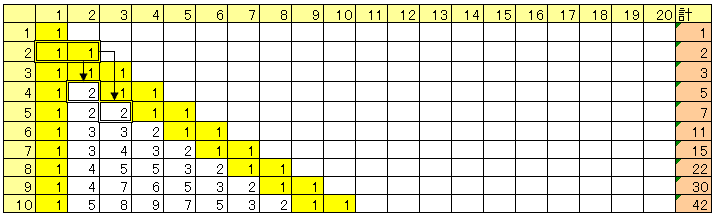
3列目の数は、3行上の1列目から3列目の数の和です。
斜めの3はすべて3行目の和になります。
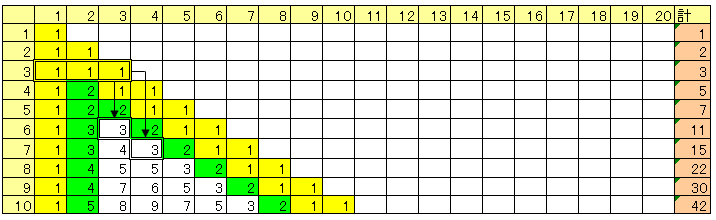
このように埋めていくと上の表ができます。
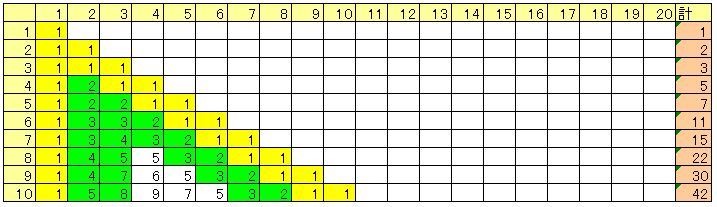
この表は次のような仕組みになっています。
P(n)をnで表すのはよく分かりませんが地道に表を作れば具体的な値は求まります。
問題３
M(1)= 1 (1)
M(2)= 2 (2, 1×1)
M(3)= 3 (3, 1×2, 1×1×1)
M(4)= 4 (4, 1×3,2×2, 1×1×2, 1×1×1×1)
M(5)= 6 (5, 1×4,2×3, 1×1×3,1×2×2, 1×1×1×2, 1×1×1×1×1)
M(6)= 9 (6, 1×5,2×4,3×3, 1×1×4,1×2×3,2×2×2, 1×1×1×3,1×1×2×2, 1×1×1×1×2, 1×1×1×1×1×1)
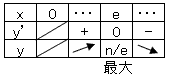
自然数nをxと(n-x)に分けてみます。
積はx(n-x)となります。
y=x(n-x) とおくと、x=n/2 のとき最大値 (n2)/4 です。
不等式 (n2)/4＞n を解くと、n が正の数のときは、解は n＞4
これは4より大きな数は、2等分した値の積が元の数より大きくなるという意味です。
次に、n=xr とします。（つまり、nのr等分がxです）
問題の意味からxrの最大を探してみます。
r=n/xなので
xn/xの最大を探します。
xn/xの自然対数をとりyとおきます。
y=log {xn/x}=n/x･log x
y’= -n/x2･log x + n/x2 = n･1/x2(1-log x)
e=2.71･･･ で1より大きいので元のxn/xもx=eのとき最大になります。
これは元の数をいくつに分けるかではなく、1つ分がeとなるように分けるとその積が最大という意味です。
eにいちばん近い自然数は3なのでなるべく3で分けるのがよいことになります。
n=6のとき、2×2×2より3×3の方が大きいことを考えると、
n≧4のとき
n=3kなら、M(3k)=3k
n=3k+1なら、M(3k+1)=4×3kｰ1
n=3k+2なら、M(3k+2)=2×3k
となります。
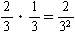
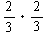
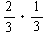
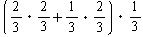
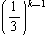
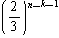
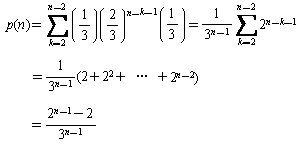
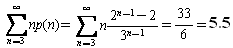
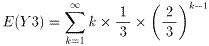
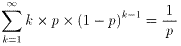となります。]