NO.1784 電磁気学Minimum-5(磁気現象) 2009.4.24. DDT
以下、 ベクトル解析Minimum-1,2,
3,4
の式は、無条件に使います。
電磁気学Minimum-4では、
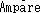 の法則とFaradayの法則を整理した結果、
真空中の電磁場の支配方程式、
の法則とFaradayの法則を整理した結果、
真空中の電磁場の支配方程式、
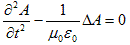 (a)
(a)
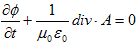 (b)
(b)
を得たので、これをMaxwellの方程式と呼びました。
ベクトルポテンシャルA,スカラーポテンシャルφと、電場E,磁束密度B(磁場H)との関係は、
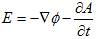 (c)
(c)
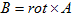 (d)
(d)
です。観測にかけられる物理量は、BとEなので、これらが最終目標となります。
しかし論理的には、(a)からAを求めれば、(b)からφが決まり、
それらから(c),(d)でBもEも計算できるので、まず(a)を解きます。
1.波動方程式を解く
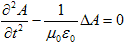 (1)
(1)
は波動方程式と言われ、偏微分方程式の中でも形式解が見つかる数少ない例です。
数少ない例なので、(1)を満たす形式解を導きます。まず、
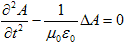 (2)
(2)
とします。これによって(1)は、
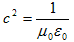 (3)
(3)
になります。
これから行う計算は長いです。
しかし、一回でも完全にやると納得できるものなので、やる事にしました。
しかしいきなり(x,y,z,t) の4変数では厳しいので、とりあえず(x,t) で考えます。
このとき(3)の微分作用素の部分だけ取り出すと、
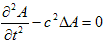
と手軽に分解できます。次のアイデアは、気づいた者勝ちです。
(x,t)→(p,s) と変数変換して、
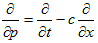 (4)
(4)
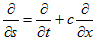 (5)
(5)
とできないか?、というのがそのアイデアです。
もしこれが可能なら、
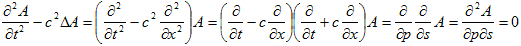
になるので、
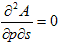
の解は、すぐみつかります。何故なら、
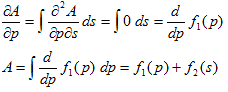 (6)
(6)
と形式解は簡単にわかるからです。ここでdf1/dp は(f1 は)、
sに対する積分定数でpの任意の関数です。f2 はpに対する積分定数で、
やはりsの任意の関数と出来ます。
(4),(5)を満たすような(p,s)=(p(x,t),s(x,t)) を求めるために、
A=A(t(p,s),x(p,s)) と考えて、(4)を考慮しつつ∂A/∂p を計算すれば、
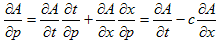
となり、中辺と最右辺の係数を比べる事により、
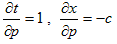
が得られます。同様に、∂A/∂s と(5)からは、
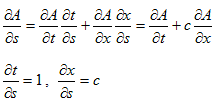
となります。まとめると(以下は、1階の完全微分を解いたのと同じです)、
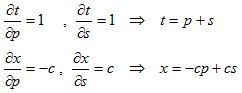
です。これらをp,sについて解けば、
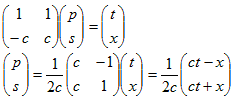
が得られます。よって(6)のf1(p),f2(s) は、
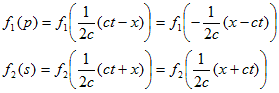
と書けますが、1/2cは定数であり、f1とf2 は任意なので、
1/2cはf1,f2 の一部とみなす事ができます。よって(6)より、
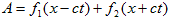 (7)
(7)
が、
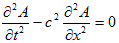 (8)
(8)
の形式解で、しかも一般解です。f1(x−ct) を波動方程式(8)の前進波,
f2(x+ct) を後退波というのは、ご存知と思います。
よって(8)は、ある波を与えます。任意関数f1,f2 の具体的な関数形は、境界条件によって決まります。
しかし(7)が(8)の一般解であると、どうしてわかるのでしょう?。
次の条件を使っています。
2階の偏微分方程式の一般解とは、その方程式を満たし、かつxとtの関数2個分の不定性を持つもの.(9)
という条件です。(9)は、2階の常微分方程式の一般解が、
その方程式を満たし、かつ任意定数2個分の不定性を持つもの.
という条件と同じだと時々言われますが(論理的にはそうかもしれませんが)、
具体的なイメージは全く別物です。だいたい(7)は、(9)の言質をそのまま満たしているわけでもないのです。
(7)が仮に、A'=f1(x)+f2(t) だったとします。
このA'は、一見「xとtの関数2個分の不定性を持つ」ように見えますが、
A'の xとt に関する偏微分をとってみると、
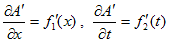
となり、それぞれの偏微分はxだけ、tだけで決まる事がわかります。
A'が本当に(x,t) の関数に関する不定性を持つなら、∂A'/∂x も∂A'/∂t も(x,t) の関数であり、
しかも任意でなければならないはずです。従って(7)は(9) の言質をそのまま満たすものではなく、
(9)はかなり曖昧な言い方である事もわかります。
(7)が(8)の一般解であるのは、以下のような具体的理由に基づきます。
任意関数f1,f2 の具体的な関数形は境界条件によって決まりますが、
1次元の波動方程式(8)の場合、それは普通、
t=0 において、A=g(x).
x=0 において、A=h(t).
という境界条件になります。ここでxとtの1変数関数であるg(x)とh(t) は任意です。
f1(x−ct) でξ=x−ct とした場合、ξの値を一個決めれば、f1 の値も一つに決まり、
ξ=一定のライン上では、f1の値も一定です。
すなわち、(x,t)平面上にf1のグラフを描けば、x−ct=ξという直線は、
(x,t)の2変数関数であるf1 の等高線になっています。
上記を(x,t)平面上の時刻t のラインで考えてみると、x≧ct では、t=0 における波形g(x) が、
(x,0)から(ct,t) だけ平行移動するのがわかります。これは、t=0 における波形g(x) が、
速度cでx方向に伝播すると読めます。
時刻tラインの0≦x<ct の領域では、x=0におけるf1の値h(t−x/c)が、
(0,t−x/c) から(x,x/c) だけ平行移動するのがわかります。
これは、x=0 における波源h(t−x/c) の値が、速度cでx方向に伝播すると読めます。特に、
t=0 において、A=0.
とすれば、時刻tラインのx≧ct では、常にf1(x,t)=0であり、
波動が存在するのは0≦x<ct の領域で、しかもその値は、
位置xでAの値はx/c秒前の波源の値と同じなので、f1(x−ct) とはまさに、x=0における波源h(t)が起こす、
x方向に前進するhの値の伝播を表わしています。
よって1次元の波動方程式(8)の解は、t=0 における全空間の波形g(x) と、
x=0 における全時間に対する波源の振る舞いh(t) で、完全に記述される事がわかります。
gとhは任意に与えられます。これがこの場合の2階の偏微分方程式の解の、関数2個分の不定性です。
この事情に関しては、2階の常微分方程式の解の不定性が、2個の任意定数に由来するのと同じですが、
「任意関数」のタイプが、偏微分方程式の種類に依存する事も見て取れます(常微分方程式に、
任意定数のタイプという考えはありません)。
1次元の波動方程式(8)の場合、任意関数のタイプは、2個の任意の1変数関数g(x),h(t) というものでした。
一方(7)において、ξ=x−ct と η=x+ct は、2つの独立した変数なので、
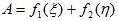 (10)
(10)
は、2個の任意の1変数関数の和になっています。変換(x,t)→(ξ,η) は変数変換なので、(10)の関数の任意性は、2個の任意の1変数関数g(x),h(t) の任意性と本質的に同等になり、境界条件に由来する解の不定性を表わしている事になります。したがって(7)は、(8)の一般解です。
境界条件に関する以上の事情に注意して、次に2次元の波動方程式、
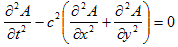 (11)
(11)
に進みます。1次元のときと同様に、微分作用素の分解を行っても、あんまり上手くいきません。
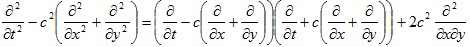
と相互作用項が出てしまうからです。このためもあってか、
2次元以上の波動方程式の形式的一般解の話は、ほとんど聞いた事がありません。
理論上(11)の解には変数分離形を仮定して、フーリエ級数かグリーン関数法に持ち込むのが普通です
(解法に一般性があるので)。実用上は、差分法や有限要素法で数値的に解きます。
これに対して1次元の波動方程式の形式的一般解は、理論上も実用上も同じくらいに有用です。
こういう状況ですが、ここでは(11)が、波動を表わす事を(電磁波が存在する事を)定性的に見たいので、
形式解の導出を試みます。
とはいえ2次元以上で形式解を扱っている本は見た事もないので、以下の議論には不備がある可能性大です。
ぜひ不備をご指摘頂ければ、幸いです。
微分作用素の分解が上手くいかないので、以下では解が見つかっちゃったぞ方式をとります。
つまりいくつかの解候補を探してきて、一般解になるかどうか判定します。
判定条件はもちろん(9)ですが、(9)を適用するためには、境界条件のタイプを決める必要があります。
2次元の場合は、
t=0 において、A=g(x,y).
x=0 において、A=h1(y,t).
y=0 において、A=h2(x,t). (12)
となります。
ここで1次元の作用素の分解を、別の角度から見てみます。
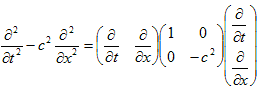 (13)
(13)
と書けます。2次形式論を用いれば、適当な線形変換(x,t)→(p,s) によって(13)は、
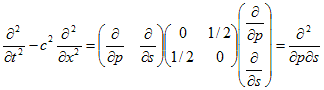
に出来るはずです。
それこそが、
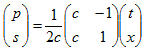
でした。
重要なのは、この方法は一般化できる事です。
(11)に対して適当な線形変換L:(x,y,t)→(ξ,η,τ) を行う事により(11)は、
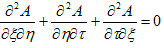 (14)
(14)
の形に出来ます。そして境界条件(12)から、
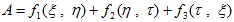 (15)
(15)
を仮定できます。ここでf1,f2,f3 は、任意の関数です。(15)を(14)に代入すれば、
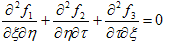 (16)
(16)
になりますが、(16)においてf1,f2,f3 は互いに関連付けられているので、
このままでは独立な任意の関数になれません。f1,f2,f3 が条件(16)を満たし、
かつ独立な任意の関数であるためには(16)は、恒等式、
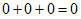
になる必要があります。よって、
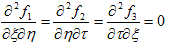 (17)
(17)
です。そうすると、それぞれの項は1次元の波動方程式なので、その一般解は、
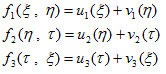
とわかっています。ui,vi は任意の関数です。これらを(15)に代入して、3つ足せば、
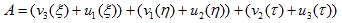
となり、ui,vi が任意関数である事を使うと結局、
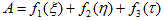 (18)
(18)
とおける事がわかります。ここでf1,f2,f3 は、再び任意の関数です。
ξ,η,τの具体的な形は、線形変換L:(x,y,t)→(ξ,η,τ) を定めれば、
出てきます。Lを定めるために、
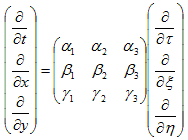 (19)
(19)
とおきます。αi,βi,γi は定数です。
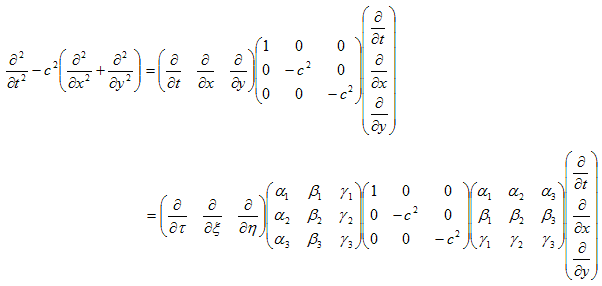
と書けます。ここでは、αi,βi,γi を面倒にしないために、
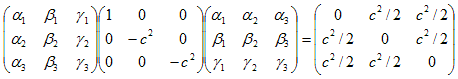 (20)
(20)
の形のものをさがします。右辺を直接計算します。
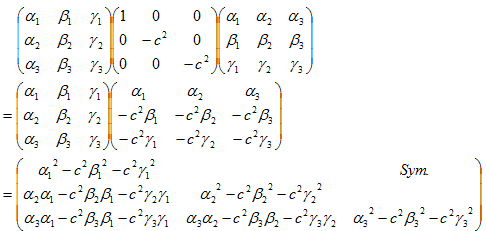
上記のSym.は、対称行列の意味です。上記と(20)により、
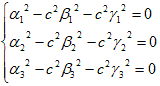 (21)
(21)
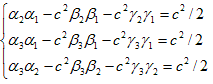 (22)
(22)
が得られます。αi,βi,γi,i=1〜3 は9個ありますが、条件(21),(22)は6個です。
よって内3個は勝手に決められます。そこで(21)から、
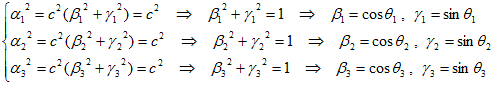 (23)
(23)
と決めます。従って(22)より、
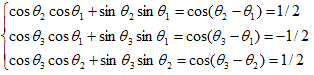
とおけるので、
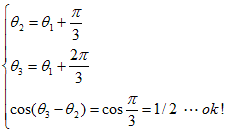
です。これより(23)から、
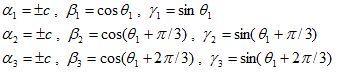
が得られます。従って(19)より、
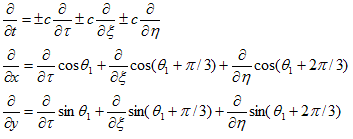
なので、
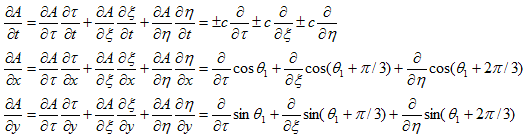
となり、
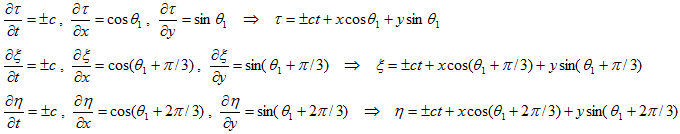
ですが、これらは、
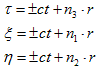 (24)
(24)
と表わせます。ここでn1,n2,n3 は、(x,y) 平面の単位ベクトルで、
互いにπ/3 だけずれていて、r=(x,y) です。(18),(24)より、2次元の波動方程式の形式的一般解は、
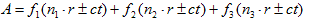 (25)
(25)
と決まります。(25)は、3方向の1次元波動の重ね合わせである事がわかります。
1次元というのは、各fi は、niへのrの正射影距離xi=ni・r で、
1次元の波動方程式の解、fi(xi±ct) と等価になるからです。
これで、目出度し目出度しと行きたいのですが、2次元の場合は解析領域の形も問題になります
(本当は1次元も)。境界条件(12)は、全空間,全時間を解析領域とした場合です。
しかし2次元の場合には、下図のような解析領域で解きたい場合もあり得ます。
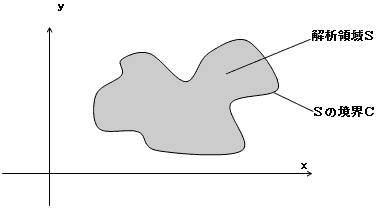
この場合の境界条件は、
t=0 で、A=g(x,y),(x,y)∈S.
C上 で、A=h(x,y,t),(x,y)∈C. (26)
となります。境界条件(26)の指定は、(12)と本質的には変わらないのですが、
(26)から直接導かれる解Aの形は、(18)ではありません。そこで次のように考えます。
波動方程式(11)と境界条件(26)のもとでS上に解Aが定まるなら、
Sの外部にも外部解A'が定まるはずです。何故なら、Sの外部でも波動方程式(11)が成り立つとして、
t=0 で、A'=g'(x,y),(x,y)∈Sの外部,g'(x,y)はC上で、S上のg(x,y)と滑らかにつながる.
C上 で、A'=h(x,y,t),(x,y)∈C. (27)
という境界条件は可能です。
従ってS上のAと滑らかにつながる、Sの外部解が存在する事になります。
S上の解とSの外部解を用いれば、t=0 における全空間のg(x,y) と、
x=0,y=0におけるh1(y,t),h2(x,t) を定義する事ができます。
よって(26)を導くような境界条件(12)の構成は可能になり、
この場合にも(25)は、一般解の資格があります。
さて、3次元、
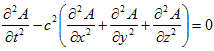 (28)
(28)
の場合です。2次元の場合で本質的な部分は尽くされている(と思える)ので、概略にとどめます。
境界条件は、
t=0 において、A=g(x,y,z).
x=0 において、A=h1(y,z,t).
y=0 において、A=h2(x,z,t).
z=0 において、A=h3(x,y,t). (29)
です。適当な線形変換L:(x,y,z,t)→(ξ,η,ζ,τ) を行う事により(28)は、
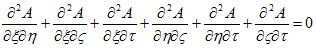 (30)
(30)
の形に出来ます。そして境界条件(29)から、
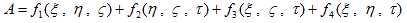 (31)
(31)
を仮定できます。ここでf1,f2,f3,f4 は、任意の関数です。(31)を(30)に代入すれば、
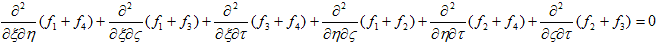 (32)
(32)
になりますが、(32)においてf1,f2,f3,f4 は互いに関連付けられているので、
このままでは独立な任意の関数になれません。f1,f2,f3,f4 が条件(32)を満たし、
かつ独立な任意の関数であるためには(32)は、恒等式、
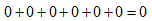
になる必要があります。よって、
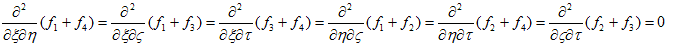
です。しかしこれでもまだ、f1,f2,f3,f4 は互いに関係しているので、例えばf1 では、
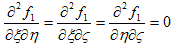
でなければなりません。1番目の条件より、
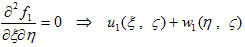
となりますが、これを2番目,3番目の条件に代入すれば、
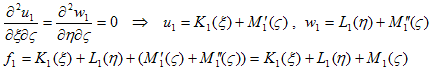
とおけます。よって、
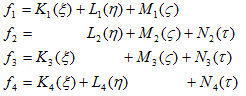
の形になり、Ki〜Ni が任意の関数である事から、あらためて、
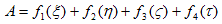
とおけます。ξ,η,ζ,τの具体的な形は線形変換L:(x,y,z,t)→(ξ,η,ζ,τ)
を定めれば得られます。ここではそれは省略しますが(もうやりたくない・・・)、
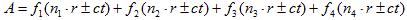 (33)
(33)
となるであろうことは、容易に想像できます。(x,y,z) 空間の単位ベクトルn1〜n4 には、
何らかの拘束条件が付くはずです。またr=(x,y,z) です。
結局3次元の波動方程式の解も、4方向の1次元の波動方程式の解の重ね合わせになっています。
従って(33)も、何らかの波動現象を表わしています。3次元の場合も、
任意の解析領域に対する考え方は同じです。