NO.2015 コロキウム室 2012.3.31. Junko
都合により、しばらくの間お休みさせてください。
これまでの皆さまの投稿、励ましのメッセージ等、多数いただきました。
心から感謝しております。
また、折りをみて、再開したいと思っておりますので、
よろしくお願いいたします。
☆Challenge!☆ 毎月の問題は、
継続しますので、ご参加ください。よろしくお願いいたします
ColloquiumNO.280
|
都合により、しばらくの間お休みさせてください。
これまでの皆さまの投稿、励ましのメッセージ等、多数いただきました。
心から感謝しております。
また、折りをみて、再開したいと思っておりますので、
よろしくお願いいたします。
☆Challenge!☆ 毎月の問題は、
継続しますので、ご参加ください。よろしくお願いいたします
[ファンデル・ワールス方程式を調べてみる]
ファンデル・ワールス方程式の名前は、一回くらいは聞いた事があると思います。 理想気体の状態方程式PV=nRT(P:圧力,V:体積,T:温度,n:気体のモル数,R:気体定数)を、 実在気体の挙動を考慮して修正したものです。最近ファンデル・ワールス方程式を調べる機会を得たのですが、 実際にやってみると必要な数学は、ほとんど高校の数Ⅲまでに含まれる範囲でした。 ただし高校数学を限界まで使う必要はあります。しかし、このような物件(?)を扱う限り、 数学技術的には高校とほとんど差はない訳です。そこで感じたのが、大学で要求される数学的な構成力でした。 別に理論を作る、という訳じゃないのですが・・・。
1.気相-液相の混在状態
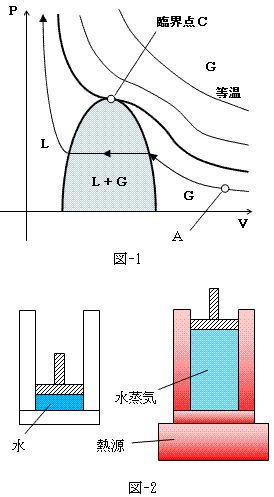 最初にファンデル・ワールス方程式と重要な関係を持つ、気相-液相の混在状態について述べます。
図-1の曲線群は、温度Tを一定にして体積Vと圧力Pを変化させた場合の、とある気体(例えば水蒸気)
の等温曲線の模式図です。ある圧力(例えば1気圧)の純粋な水蒸気というのは考えにくいかも知れませんが、
図-2に示したように一定体積の水にぴっちりとピストンで蓋をし、それを十分熱容量の大きい一定温度の熱源に接触させて、
全部気化したらできあがりという、他愛もないものです。熱に強い注射器さえあれば実現できます。
図-2の右の状態が、図-1のA点だったとします。
最初にファンデル・ワールス方程式と重要な関係を持つ、気相-液相の混在状態について述べます。
図-1の曲線群は、温度Tを一定にして体積Vと圧力Pを変化させた場合の、とある気体(例えば水蒸気)
の等温曲線の模式図です。ある圧力(例えば1気圧)の純粋な水蒸気というのは考えにくいかも知れませんが、
図-2に示したように一定体積の水にぴっちりとピストンで蓋をし、それを十分熱容量の大きい一定温度の熱源に接触させて、
全部気化したらできあがりという、他愛もないものです。熱に強い注射器さえあれば実現できます。
図-2の右の状態が、図-1のA点だったとします。
A点からピストンを押して体積を減少させて行くと、理想気体の状態方程式から予想されるように、
圧力Pは上昇します。図-1の太実線の下側の、G(Gas)でマークした領域にある矢印曲線です。
このとき熱源の熱容量が十分大きく、圧縮速度が十分遅ければ、容器も水蒸気の温度も、
熱源の一定温度Tに保てるので、圧縮は等温過程になります。
ところが、ある体積に達すると、水蒸気は液化を始め、圧力は変化しなくなります。
L+Gでマークしたハッチ領域です。LはLiquidの略です。ハッチ領域では、
圧力一定になるように水蒸気が液化し、気相の(水蒸気の)体積を減らしたと考えられます。
図-1の水平線は、液化しなかった水蒸気に関するものです。このときも先の理由から、等温圧縮が可能です。
L+Gの左端に達すると、水蒸気は全部液化し、太実線の下側のLでマークされた領域に入ります。
そこには水(お湯かも)しかなく、そこにある矢印線は液相の等温曲線と考えられます。
液体(液相:水)の非圧縮性は非常に大きいので、ここの等温曲線は極端な単調減少性を持ちます。
太実線は臨界曲線と言われ、これより高温の等温曲線では、気相はいくら圧縮しても液化しません。
臨界曲線と気相-液相の混在領域の接点を、臨界点と言います。以上が、気相-液相の混在状態についての概要です。
2.ファンデル・ワールス方程式
ファンデル・ワールスは、この謎(?)を解くために、次の形の理想気体からの状態方程式の修正を提案します。

です。排除体積bの意味は明らかと思います。気体も分子や原子の集団なのだから、
圧縮できるところまで圧縮した時の物質の固有体積をbとすれば、(2)の適用範囲はb<Vと考えるべきだ、という意味です。
V→bの時は、P→∞になります(理想気体と同じ)。
aの意味は一議論必要なのですが(たぶん高校では無理)、
分子間力を非常な短距離で有効な重力のようなものと考えると、この形になるとだけ、ここでは述べておきます。
(1)と(2)を比べると、aはモル数nの2乗に比例し、bはnに比例し(これは当然と思います)、
見落とされがちですが、気体定数Rもnに比例します。Rがnに比例する事については、
もしかすると高校範囲でも説明可能と思います。
3.ファンデル・ワールス方程式の概形
ファンデル・ワールス方程式2.(2)を、圧力Pについて解くと、次の形に変形できます。
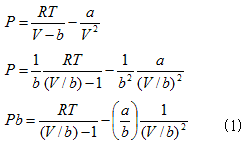
ここでa,bが気体に固有の定数である事を考慮すると、ファンデル・ワールス方程式の挙動は、
一般的に次のようになるはずです。
一定のTに対し、V/b~1の近傍では、(1)の右辺1項目が2項目に対して優勢なので、V/bに対して単調減少。V/bが十分大きくても、(1)の右辺1項目と2項目はともに単調減少でPbは0に近づくが、2項目の方が速く減少するから、0へはPb>0の方から近づく。中間領域では、1項目と2項目のせめぎ合いで、Pbは極小や極大を持ちそうだが、a/bが気体に固有の定数で、Tはいくらでも大きくできる事を考えると、十分大きいTに対してPbは、V/bに関して単調減少の可能性がある(全て高校範囲)。
上記のようなグラフの概形は、図-1のようなものだと想像できます。図-1では極値は2個のように描いています。極値が何個出てくるか確認するために、(1)を(2.(2)を)体積Vについての方程式とみなしますが、こう思い立つのは、やはり大学の発想かも知れません。
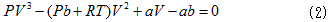
(2)はVについての3次方程式なので、与えられたPについて最大3個の解を持ちます。V/b→1でP→∞,V/b→∞でP→0,P>0(当然)を考慮すると、極大が1個でも出ればペアになる極小が必要で、極大と極小の間にPを設定すれば、Pの上下限における挙動から、(2)は3個の解を持つはずです。よって図-1の臨界曲線の下側の等温曲線の概形は、(1)が本当に極値を持つなら妥当という事になります。
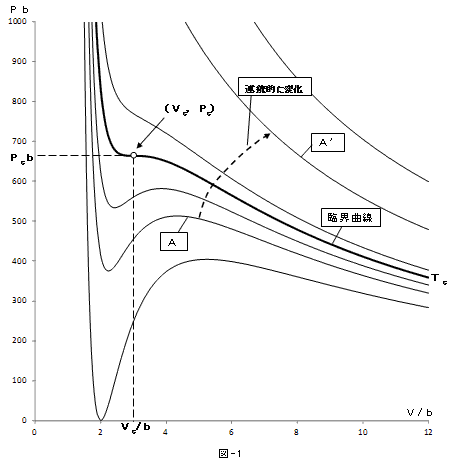
図-1の臨界曲線が、1.で述べた臨界曲線と同じものかどうかは、まだわかっていませんが、 図-1に、Tcでマークした等温曲線が現れるであろうという事も、じつは定性的な想像です。 理由は4つあります。Tが十分大きければ極値はないであろうという事、その概形は理想気体のものに近づくであろう事(2.(2)は、理想気体の修正だから)、 Tが大きいほど等温曲線は上にずれる事(理想気体の性質)。そして4つ目が、例えば図-1の曲線Aは、Tを連続的に大きくすれば、 曲線A'へ連続的に形を変えるはずだ、という想像です。連続的なので境い目があるはずです。 それを曲線Tcとすると、Tcより上で(1)は極値を持たず、下では一組の極値ペアを持ち、Tcは両者の境い目なので、Tc上で極値ペアは合体するはずです。 これは極小値=極大値という事なので、(2)は3重根を持つ事になります。3重根をV=Vc,その時の圧力,温度を、P=Pc, T=Tcで表わせば、3次方程式の解と係数の関係より、

と計算できます。こうして臨界体積,圧力,温度、Vc,Pc,Tcは、
高校数学の技術でほとんど計算する事もなく決まります。大学式の発想で、定性的想像を逞しくしたためです。
しかし臨界状態(Vc,Pc,Tc)を計算できた以上、その想像は正しかった事になります。
ところで(6),(7),(8)を眺めていると、無次元量、

が得られます。(13)を対応状態方程式と言います。物質固有の定数a,bなどに関わる事なく、
何でもかんでも無次元化して扱おうというのも、大学の発想です。ファンデル・ワールスが(10)を導いた仮定は、
ある程度普遍的に正しいと考えられます。そうすると対応状態方程式(13)は、その仮定の適用範囲内にある全ての物質で普遍的な、
(10)の一般化です。
(13)と(10)を比較すると、対応状態方程式の中で、aは3に、bは1/3に、Rは8/3に規格化されているのがわかります。臨界状態(Vc,Pc,Tc)は、もちろん(1,1,1)です。
4.ところがファンデル・ワールス方程式には問題がある
ところがファンデル・ワールス方程式には、大問題があります。3.(13)を規格化された圧力ξについて解き、
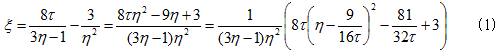
の最右辺の符号を、1/3<ηの範囲で調べてみると(分子が2次関数なので可能)τ<27/32の範囲で、ξは必ず負になる部分を持ちます。
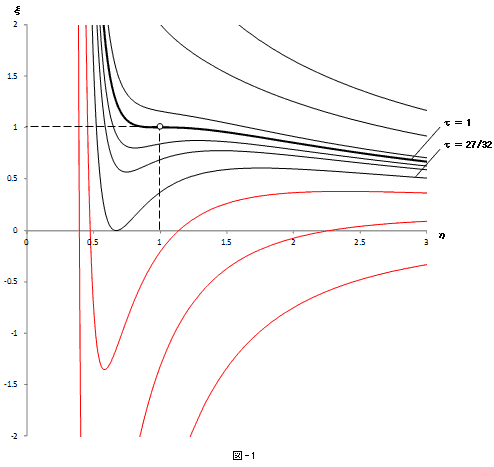
図-1の赤ラインに対して、果たして物理的意味はあるのか、と問うのは正当です。何故なら、状態方程式の圧力が負になるという事は、物質が自立できない事を示し、ある体積より小さい範囲では、物質は自然にどこまでも潰れる事になるからです(ブラックホールじゃあるまいし・・・)。ファンデル・ワールス方程式は理想気体の状態方程式の修正なので、圧力ξの零点は真空,温度0<τは絶対温度です。ξを1気圧に対する相対圧力とみなしたり、τに適当な制限を設ける事はできません。τ<27/32の範囲でξ<0になるケースは、避けられない訳です。この事実はファンデル・ワールス方程式が、一つの近似式である事を端的に示します。
これには悩みました。3.(10)のa,bは、気体の2つの状態がわかれば計算できるので、理科年表なんかを持ちだして計算してみたところ、τ=1は摂氏に直して365(℃),τ=27/32は265(℃)となり、100(℃),1気圧の水蒸気なんか、少し圧縮したらすぐに圧力負になり兼ねません。もっとも100(℃),1気圧,1mol(1/18(g))の水蒸気の体積は、η=330くらいなので、図-1のξが負の領域は余り目立たない事にはなりますが・・・。でもη~1程度になるモル数だって可能です。
それでも次のように想定する事はできます。現実の物質がファンデル・ワールス方程式に厳密に従うとして、ξが負になり物質が自立できなくなった時に、人間が人工的に負圧(真空以下の圧力って、どう作るかは問いません)を与えて、本当にファンデル・ワールス方程式を成り立たせた、という想定です。ここからトリビアルでない結果を引き出せなければ、この想定は無意味ですが、そうではないのです。その一つが、Maxwellの規則の適用です。
5.気相-液相の混在領域を導く
例えばτを水蒸気の等温曲線とし、ξが負にならないケースで、
水蒸気は実験的に図-1に示すような挙動を実際に示します。
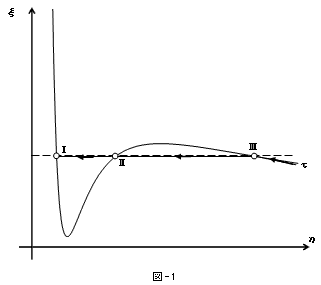
1.で述べたように、十分大きな体積の純粋な水蒸気を圧縮して行くと圧力は次第に上昇し、ある圧力に達したときに水蒸気は、液化を始めます。それが図-1のⅢの点です。さらに体積を減少させると、圧力は一定のまま液化は進行し、Ⅱを通過してⅠにいたります。
この現象は、圧力を一定に保つように水蒸気が液化して行く過程だと言えます。Ⅲ→Ⅱ→Ⅰの直線は、気化したままの水蒸気の状態を表わしたもので、水蒸気のモル数は減少する事になります。モル数が減少した状態に対しても、ファンデル・ワールス方程式は成り立っているはずです。
そうするとまず興味があるのは、ある与えられたξ,τに対してファンデル・ワールス方程式を満たすようなモル数の減少は可能か、という事です。2.(1)に戻り強引に計算すれば明らかなのですが、問題はこの状態を手に取ったように表現したい、という点です。対応状態方程式の規格化を利用します。
最初のモル数をnとし、それがkn,0<k≦1に減ったとして、対応状態方程式を書き直します。臨界状態をa,bで表わした3.(6),(7),(8)で、aはn2に、bとRはnに比例する事に注意すれば、

で、明らかに対応状態方程式は、任意の0<k≦1で成り立ちます。
ここで使った数学技術は実際のところ、割り算とη方向へのグラフの縮小/拡大だけです。モル数がk倍に変化すれば対応状態方程式のグラフは、η方向へk倍に拡大されるので、ηもそれに伴ってk倍されれば対応状態方程式は不変なので、k倍のモル数に対応する状態は、必ずファンデル・ワールス方程式を満たすという発想です。計算技術は簡単ですが、これはやはり大学の発想だと思います。
こっからはしばらく、大学の知識を使います。直線Ⅲ→Ⅱ→Ⅰで表わされる過程は、じつは可逆過程です。直線Ⅲ→Ⅱ→Ⅰは、液化していない水蒸気の状態変化を表わしています。それらに対しては、図-2に示すような可逆実験が原理的には設定可能だからです。
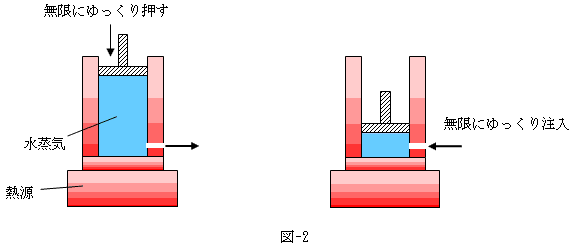
一定温度,一定圧力の純粋な水蒸気が入った容器のどこかに無限小の穴をあけ、ピストンを無限にゆっくり押してやれば、一定温度と一定圧力を保ったまま、水蒸気を望むままに排気できます(左側)。この過程は、直線Ⅲ→Ⅱ→Ⅰの液化していない水蒸気の状態変化と同等です。排気された水蒸気が液化した訳です。反対に右側では、無限にゆっくり注気し、Ⅰ→Ⅱ→Ⅲと一定温度と一定圧力を保ったまま、Ⅲの状態に戻してやる事が可能です。このように往復可能な過程を可逆過程と言います。
一方Ⅰ,Ⅱ,Ⅲを通る1個のファンデル・ワールス方程式で表わされる状態も、実験条件を十分に整えてやれば実現可能である事が、知られています。状態方程式を満たす過程は、全て可逆過程です。
よって図-3に示した、Ⅰ→A→Ⅱ→B→Ⅲ→Ⅱ→Ⅰのサイクル上の全ての状態はファンデル・ワールス方程式を満たすので、サイクルは可逆過程です。
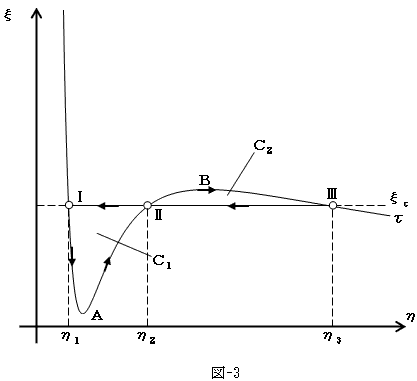
図-3のサイクルは等温状態で行われるので、等温可逆サイクルでもあります。任意の過程のエントロピーsは、

をηで積分すれば、(8)を考慮して、
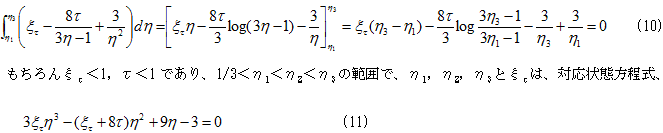
を満たします。(11)は、ξτ,η1,η2,η3について3個の条件なので、(10)と合わせて4個の条件から、与えられたτに対する4個の未知数ξτ,η1,η2,η3は、(10)と(11) から決定できるはずです。
以上の関係が、ξが負になる場合にも正しいと仮定すると、任意のξτ<1,τ<1に対して、
気相と液相が混在する範囲を、定性的に決定できる可能性が出てきます。ここではそれを、数値的に実行しますが、
ここは本当に大学生の構成力が試されるところだと思います。
まず(11)が(重根も含む)3実根を持つためには、等温曲線τの極小値ξLと極大値ξuの間に、
ξτがなければなりません。
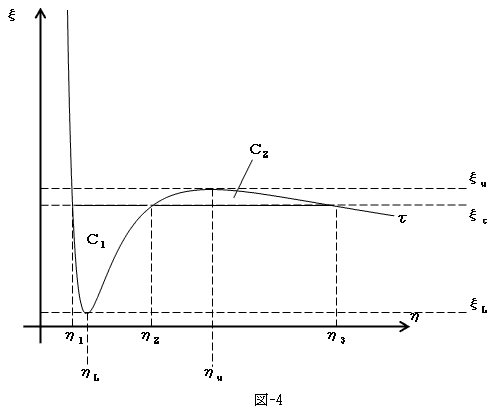
そこで0<τ<1,1/3<ηの範囲で、4.(1)の極小値,極大値を求めます。4.(1)をηで微分し、
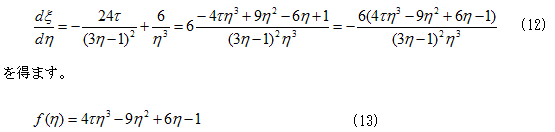
とすれば、

の解になります。よって図-4より、
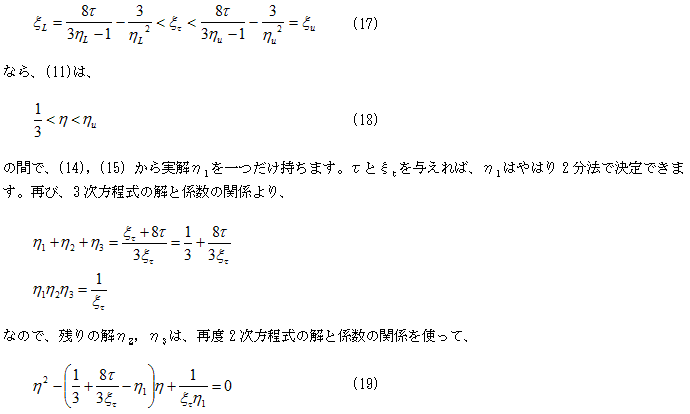
の解になる事がわかります。
よってτとξτを与えればη1,η2,η3は計算できるので、(10)も計算できます。従ってτを与えて、(17)の区間でξτに関する2分法を実行すれば、ξτも決定できます。(17)におけるξτの一意性は、図-4の面積C1,C2が、ξτについて単調増加,単調減少である事から明らかです。
後は、十分細かい刻み値で0<τ<1を分割し、全てのτのサンプル値に対して、以上の3回の2分法手続きを適用すれば、(10)を満たすようなξτ,η1,η3を、τの各サンプル値に対して十分細かく決定できる事になります。補足の留意点としては、ξL<0となった場合、ξ<0の領域には(10)を満たすξτは存在しないので、ξτの2分法の下限として、ξτ=0を設定する必要があるという事です。
2分法は、ちょっと変わった漸化式に過ぎません。そして上記で述べた計算手順の全体も、解を得るための繰り返し計算について述べただけなので、少々複雑な漸化式の説明に過ぎません。特殊な計算技術などどこにも出てきません。そう考えると、技術的には高校範囲です。
しかし上記の説明から、τを刻む最外殻Loopを想像し、その中にある一つの2分法Loopと、2重にネストした2分法Loopを、あっさり想像できたなら、もう十分大学学部レベルの数値計算プログラマーとして食っていけると思います。これが数学的構成力ではないでしょうか?。
以上の方針のもとに求めた図が、下図です。プログラム環境としては、Excelマクロを使いました(グラフにするのが便利なので)
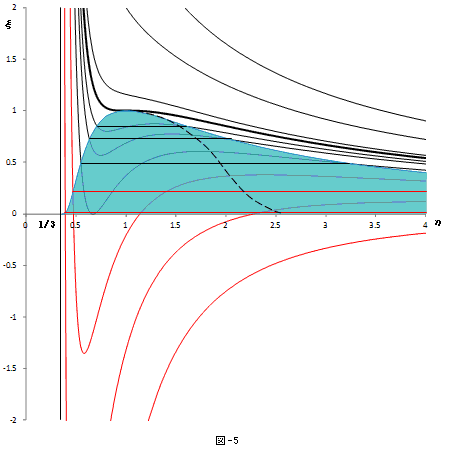
青色の領域は、τ=0でη=1/3とη=∞の上下限を持ちます。実験的には点線で示したような領域になるそうですが、ξ<0に対してもMaxwellの規則を認める事によって、とにかく気相-液相の混在領域を、定性的には再現できます。また通常の過程では、気相の液化が起こるので、気体の圧力は決して負にならない事もわかります。
気相-液相が混在する直線の下限で、実験的には全ての気相が液化します。従って混在領域の左側と、臨界曲線、およびη=1/3に囲まれた領域は、液相の状態方程式を表わしていると考えられます。そうすると、液相(液体)の体積変化の温度依存性も、ファンデル・ワールス方程式から定性的には、予想できる事になります。それ以外の領域で物質は、気相として振る舞います。特に臨界曲線より上の温度では、液化しません。
ここで「物質は」と言ったのは、ファンデル・ワールス方程式のモデルが近似として正しい限り、臨界状態で規格化した対応状態方程式は、どんな物質の相においても近似的に成立すると考えられるからです。という事は、固体-液相間の事情も同じになります。Maxwellの規則は、熱力学に基づいた一般的規則なので。
このようにファンデル・ワールス方程式は、以上の話だけでなく、色々な物性物理の謎を定性的に理解するためのツールとして、前代未聞に有効でした。式が簡単であるというのは、数学的な観点としてはとても重要だと思います。
そのためにファンデル・ワールス方程式には、圧力が負になるという致命的な欠陥があるにも関わらず、「気体と液体の連続性について」という論文で、ファンデル・ワールスはノーベル賞を取ります。ノーベル賞委員会は、確かにプロですね。
ところで固体-液相間にも同じ事情が成り立つならば、図-5のどこかに固体-液相の混在領域が現れるはずです。氷点を下回った温度でも液体でいる水は、過冷却水などと言われ現実に存在します。過冷却蒸気は、図-5のどこでしょう?。
そういう事を考えると、固体-液相の混在領域を調べるためには、液体のファンデル・ワールス方程式があれば良いのです。
その時には「それと」気体と液体のファンデル・ワールス方程式の関係は?、などが問題になります。そういう事ができたとき、先人の二番煎じは猿でも出来ますが、「気体と液体と固体の連続性について」を語った事になります。ちょっと、調べてにようかなぁ~、という気にはなりました。誰かがやってるはずなので。
●準備
○頂点が放物線上にある三角形の面積について
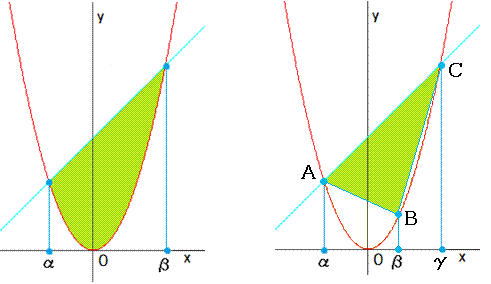
y=ax2 のグラフと直線が交わってできる部分の面積(上の左黄緑色部分)は、
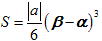 です。
です。
これを使うと右の図で△ABCの面積は、
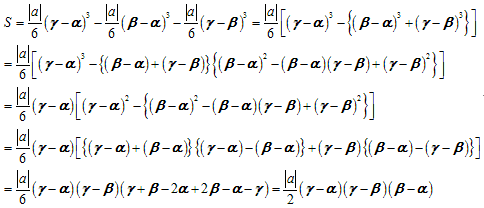
○原点と他2点で決まる三角形の面積について(ついでに)
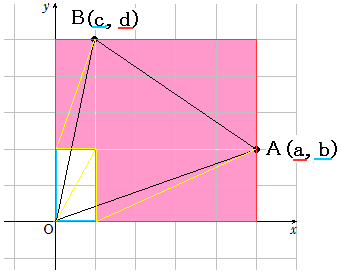
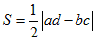
これを使うと、上の右の△ABCの面積は、
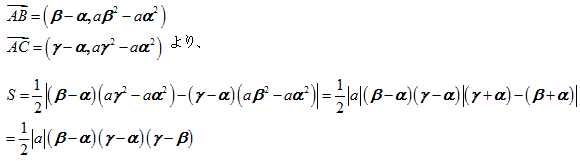
○放物線上の2点を結ぶ直線の平均変化率と微分係数
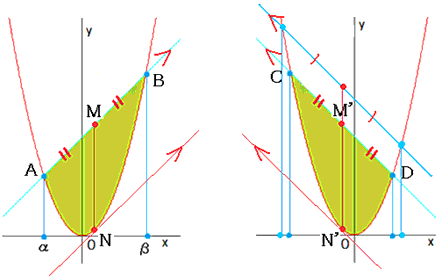
放物線上の2点A,Bを結ぶ直線の平均変化率は、その中点Mからx軸に垂線を下ろしたとき、 放物線と交わる点Nでの微分係数と等しくなります。
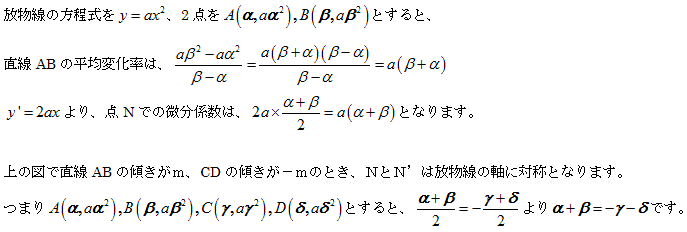
●解答
1.問題1
(1)放物線の方程式が y=2x2 なので、3点は、A(1,2),B(2,8),C(4,32) です。
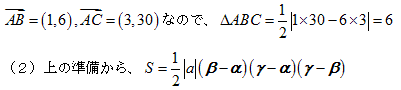
問題2
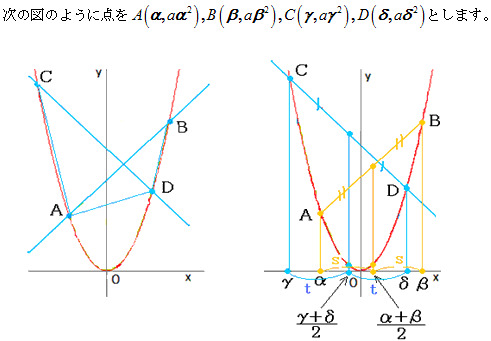


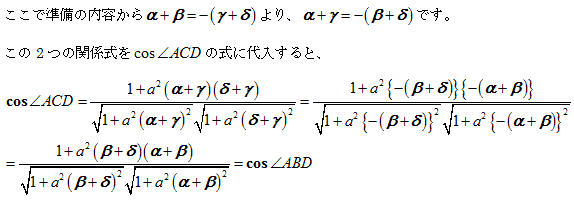
故に、 となり4点A、B、C、Dは同一円周上にあります。

問題1
(2)から解きます
求める三角形の面積をA
放物線を
y=ax2+bx+c・・・[1}
xがα,β,γのときの放物線のy座標をy1,y2,y3
(α,y1)と(γ,y3)を通る直線とy=βの交点を(β,y4)
(α,y1)、(γ,y1)、(γ,y3)を頂点とする直角三角形をA1
(α,y1)、(β,y1)、(β,y4)を頂点とする直角三角形をA2
とします。
次の関係が成り立ちます 問題2
P1とP2の中点は ( (m-b)/2a , m(m-b)/2a )
y1=aα2+bα+c・・・[2]
y2=aβ2+bβ+c・・・[3]
y3=aγ2+bγ+c・・・[4]
変形して
y2-y1=a(β2-α2)+b(β-α)=(β-α)(a(β-α)+b)・・・[5]
y3-y1=a(γ2-α2)+b(γ-α)=(γ-α)(a(γ-α)+b)・・・[6]
y3-y2=a(γ2-β2)+b(γ-β)=(γ-β)(a(γ-β)+b)・・・[7]
A2はA1に相似なので
(y4-y1)/(y3-y1)=(β-α)/(γ-α)
y4=(y3-y1)(β-α)/(γ-α)+y1・・・[8]
上式に[6]を代入すると
y4=(γ-α)(a(γ-α)+b)(β-α)/(γ-α)+y1
さらに両辺からy2を引くと
y4-y2=(γ-α)(a(γ-α)+b)(β-α)/(γ-α)-(y2-y1)
上式に[5]を代入すると
y4-y2=(γ-α)(a(γ-α)+b)(β-α)/(γ-α)-(β-α)(a(β-α)+b)
y4-y2=(β-α)((a(γ-α)+b)-(a(β-α)+b))
整理して
y4-y2=a(β-α)(γ-β)・・・[9]
求める三角形の面積Aは
A=(y4-y2sub>)(γ-α)/2・・・[10]
で表されるので[9]を代入して
A=a(β-α)(γ-β)(γ-α)/2・・・回答
(1)
(2)の結果に代入して
A=2(2-1)(4-2)(4-1)/2=6・・・回答
傾きが±mである2直線と放物線の相対的な位置関係をフリーにとればよいので
2直線の交点を原点に取り
放物線 y=ax2+bx+c・・・[1]
直線 y=mx ・・・[2]
y=-mx ・・・[3]
とします。
[1]と[2]を連立し交点を求めP1,P2(xの小さいほうから)とすると
P1 ( (m-b-((m-b)2-4ac)0.5)/2a , (m(m-b-((m-b)2-4ac)0.5))/2a )
=(P1x,P1y)
P2 ( (m-b+((m-b)2-4ac)0.5)/2a , (m(m-b-((m-b)2-4ac)0.5))/2a )
=(P2x,P2y)
[1]と[3]を連立し交点を求めP3,P4(xの小さいほうから)とすると
P3 ( (-(m+b)-((m+b)2-4ac)0.5/2a , (m(m+b+((m-b)2-4ac)0.5))/2a )
=(P3x,P3y)
P4 ( (-(m+b)+((m+b)2-4ac)0.5/2a , (m(m+b-((m-b)2-4ac)0.5))/2a )
=(P4x,P4y)
P3とP4の中点は (-(m+b)/2a , m(m+b)/2a )
P1とP2の中点を通り傾きが-1/mの直線はP1、P2から等距離で
y=-x/m+m(m-b)/2a+(m-b)/2am ・・・[4]
P3とP4の中点を通り傾きが1/mの直線はP3、P4から等距離で
y=x/m+m(m+b)/2a+(m+b)/2am ・・・[5]
[4]と[5]を連立し交点を求めPoとすると
Po ( -(1+m2)b/2a , (1+m2)/2a ) =(Pox,Poy)
P1,P2,P3,P4が同一円周上にあるとすればPoはその円の中心となります
線分P1Po=線分P2Po,線分P3Po=線分P4Poは明らかなので
線分P1Po=線分P3Poを示せばP1,P2,P3,P4が同一円周上にあると言えます。
そこで
((P1x-Pox)2+(P1y-Poy)2)0.5
((P3x-Pox)2+(P3y-Poy)2)0.5
を計算すると何れも
((b2+1)(m2+1)2-4ac(m2+1))0.5/2a ・・・[6]
となります
よってP1,P2,P3,P4が同一円周上にありその半径は[6]です。
以下すべて、放物線の頂点を原点とするが、その他の場合も平行移動により得られるので等価でり、一般性は失われない。
問題1
(1)これは(2)で一般の場合を示せば、その式において、a=2、α=1、β=2、γ=4とすればよいので略。
(2)便宜のため、図1のように長さを定める。
まず、△ABC = 1/2 × あ × い ・・・[1]
ここで、直線ABの式 y = a(α+γ)x - aαγ より
あ = {a(α+γ)β - aαγ} - aβ2 = -a{β2 - (α+γ)β + αγ} = -a(β-α)(β-γ) =a(β-α)(γ-β) = a × う × え ・・・[2]
[1][2]より、△ABC = 1/2 × a × い × う × え …(答)
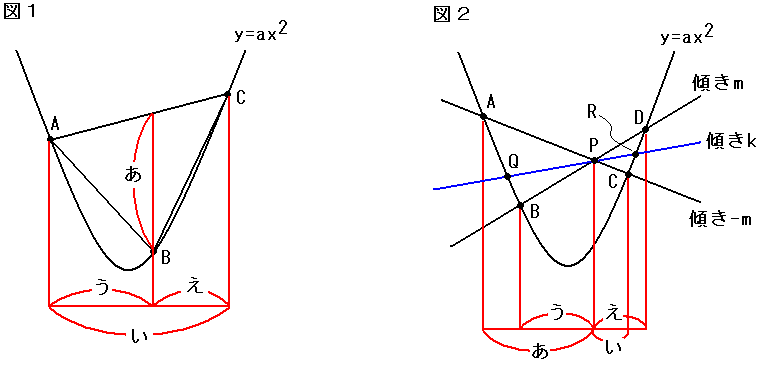
問題2
便宜のため、図2のように長さを定める。
題意を示すための準備として、まず、あ × い = う × え …(☆)を示す。
点P(s,t)を通る直線の傾きをkとすると、この直線の式は、y = k(x-s) + t であり、
直線と放物線との交点Q、Rのx座標をそれぞれu、vとすると
ax2 = k(x-s) + t ax2 - kx + sk - t = 0
解と係数の関係より、u+v = k/a、uv = (sk-t)/a
このとき、(s-u)(v-s) = -(s-u)(s-v) = -{s2 - (u+v)s + uv} = -{s2 - (k/a)s+ (sk-t)/a} = t/a - s2 = (一定)
(s-u)(v-s)の値はkの値によらず一定であることから、(☆)が成り立つことは示された。
つぎに、傾きmと傾き-mの正射影より、PA:あ = PC:い = PB:う = PD:え …(★)が成り立つ。
(☆)(★)より、PA × PC = PB × PD が成り立ち、方べきの定理の逆から、題意は示された。
