Weekend Mathematics／コロキウム室／1999.7〜9／NO.70

コロキウム室



NO.605 '99 9/1Junko源氏香（２）

香の種類に関係なく形の違いだけを数え上げていけばいいということなので、 以下のように場合分けします。
同じ種類の香がいくつあるかで場合わけです。
香の形場合の数
５１
４−１５Ｃ１＝５
３−２５Ｃ２＝１０
３−１−１５Ｃ３＝１０
２−２−１５Ｃ２×３Ｃ２／２！＝１５
２−１−１−１５Ｃ２＝１０
１−１−１−１−１１
合計５２




NO.606 '99 9/2水の流れジャンケン（１）

西欧には、何かを決めるときコインでの表・裏を当てて決めています。
それに対して、日本では順番や鬼を決めるとき、ジャンケンで決めています。
２人でやったとき、アイコ（同じ、グー、チョキ、パーを出したとき）でない限り、 すぐに勝負がつきます。
３人でやったとき、全員同じもの出したり、３人が異なるものを出したりすると、 アイコでなかなか勝負がつかないことがあります。
そこで、問題です。何人かでジャンケンをした場合１回で勝負がつく平均回数を求めてください。
２人、３人、４人、５人、６人、・・・、１０人のときまで、調べてください。
一般のＮ人のときは、どうなるのでしょう。私はまだ、求めていません。」



NO.607 '99 9/4浜田　明巳ジャンケン（２）

Ｎ人でジャンケンをした場合，次の３つの場合，１回で勝負がつきます．
１人がグー，(Ｎ−１)人がチョキ
１人がチョキ，(Ｎ−１)人がパー
１人がパー，(Ｎ−１)人がグー
グーを０，チョキを１，パーを２で表し，パソコンの乱数を使って， 平均値を求めるプログラム（エクセル・マクロ）を作りましたので，紹介します．
このプログラムによると，試行回数１００００００回で，
Ｎ平均
20.667106
30.334096
40.148154
50.061988
60.024455
70.009632
80.003711
90.001371
100.000487
110.000188
120.00006
130.000019
140.000011
150.000004
160.000002
170
180
190
200

となります．実際の答Ｎ／３(N-1)と比べてもまずまずの値でしょう．
ただし１７回以上では平均は０となってしまいます．
試行回数をもっと多くとれば，それなりに近い値となるでしょうが， 計算終了まで大変な時間がかかってしまいます． 

Sub janken()
    '何人かでジャンケンをした場合１回で勝負がつく平均回数を求めよ．
    Dim j, n, n_max, katta As Integer: n_max = 20
    Dim shikoukaisuu, shikoukaisuu_max, kaisuu(20) As Long
    shikoukaisuu_max = 1000000
    For n = 2 To n_max: kaisuu(n) = 0: Next
    Dim a(20), b(2) As Integer
    Randomize Timer
    Range("B1").Select
    ActiveCell.FormulaR1C1 = "計算中"
    For n = 2 To n_max
     Range("A1").Select
     ActiveCell.FormulaR1C1 = "Ｎ＝" + Str$(n)
     For shikoukaisuu = 1 To shikoukaisuu_max
      For j = 0 To 2: b(j) = 0: Next
      For j = 1 To n: a(j) = Int(Rnd * 3): b(a(j)) = b(a(j)) + 1: Next
      katta = 0
      For j = 0 To 2
       katta = katta - (b(j) = 1 And b((j + 1) Mod 3) = n - 1)
      Next
      kaisuu(n) = kaisuu(n) + katta
     Next
    Next
    Range("A3").Select
    ActiveCell.FormulaR1C1 = "Ｎ"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "回数"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "試行回数"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "平均"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "N/3^(N-1)"
    For n = 2 To n_max
     SendKeys "{down}", True
     For j = 1 To 4: SendKeys "{left}", True: Next
     ActiveCell.FormulaR1C1 = n
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = kaisuu(n)
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = shikoukaisuu_max
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = kaisuu(n) / shikoukaisuu_max
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = n / 3 ^ (n - 1)
    Next
    Range("A3").Select
End Sub




NO.608 '99 9/5Junkoジャンケン（３）

Ｎ人で１回だけジャンケンをしてそれがアイコになる確率をＰＮとしてこれを求めますす。
まずＮ人でジャンケンをするとそれぞれが独立に３通りの手の出し方があり全部で３Ｎ通りになります。
逆にアイコにならない場合を考えます。
Ｎ人の手の出し方が、グ−、チョキ、パ−のうちただ２つの手しか出ない場合です。
これが３通りです。
たとえばグ−とチョキだとします。
Ｎ人それぞれがグ−とチョキのどちらかを出すわけですから、全部で２Ｎ通り。
ただし、全員がグ−を出す場合と全員がチョキを出す場合の２通りについてはまずいので、これを排除します。
以上のことにより、



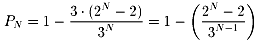
Ｎ人でジャンケンをして何回目で勝負がつくか、いいかえれば何回目でアイコが途切れるかを ｆ(Ｎ)とします。
その期待値は以下のような無限級数になります。




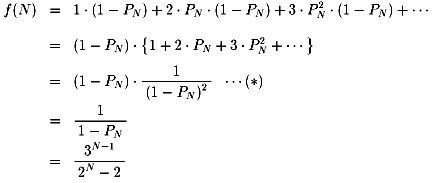
(*)について
０＜ｒ＜１に対して、
Ｓｎ＝１＋２ｒ＋３ｒ２＋４ｒ３＋　　　・・・　＋ｎｒｎ−１　　　　　　　　・・・(1)
ｒＳｎ＝　　　ｒ＋２ｒ２＋３ｒ３＋４ｒ４＋・・・＋(ｎ−１)ｒｎ−１＋ｎｒｎ　・・・(2)

(1)-(2)より、


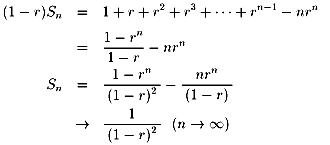
NO.607で、浜田　明巳さんはただ１人の勝者がでる場合としていますが、 私はアイコ以外(つまり何人かの勝者と何人かの敗者に分かれる)こととしました。

ジャンケンについては「IDAHO POTATE」さんが、 気まぐれ数学談話室の中で話題にしていらっしゃいます。
なかなか興味深い提案もありますので、是非のぞいてみてください。





NO.609 '99 9/8浜田　明巳ジャンケン（４）

前回，私の解答に誤りがあったようなので，訂正します．申し訳有りませんでした．
Ｎ人でジャンケンをした場合，出た目が２種類のみの場合，１回で勝負がつきます．
グーを０，チョキを１，パーを２で表し，パソコンの乱数を使って，平均値を求めるプログラム （エクセル・マクロ）を作りましたので，紹介します．
このプログラムによると，試行回数１００００００回で，
Ｎ平均
20.666726
30.666953
40.51869
50.369903
60.255203
70.172508
80.117154
90.077759
100.051915
110.034605
120.023291
130.015396
140.010256
150.007055
160.004571
170.003048
180.002031
190.001405
200.000898

となります． 試行回数をもっと多くとれば，いい近似値となるでしょうが， 計算終了まで大変な時間がかかってしまいます． このくらいが妥当でしょう．
このプログラムは，前回のプログラムより簡単に作成することが出来ました．

Sub janken2()
    '何人かでジャンケンをした場合１回で勝負がつく平均回数を求めよ．
    Dim j, n, n_max As Integer: n_max = 20
    Dim shikoukaisuu, shikoukaisuu_max, kaisuu(20) As Long
    shikoukaisuu_max = 1000000
    For n = 2 To n_max: kaisuu(n) = 0: Next
    Dim a(20), b(2) As Integer
    Randomize Timer
    Range("B1").Select
    ActiveCell.FormulaR1C1 = "計算中"
    For n = 2 To n_max
     Range("A1").Select
     ActiveCell.FormulaR1C1 = "Ｎ＝" + Str$(n)
     For shikoukaisuu = 1 To shikoukaisuu_max
      For j = 0 To 2: a(j) = 0: Next
      For j = 1 To n: a(Int(Rnd * 3)) = 1: Next
      kaisuu(n) = kaisuu(n) - (a(0) + a(1) + a(2) = 2)
     Next
    Next
    Range("A3").Select
    ActiveCell.FormulaR1C1 = "Ｎ"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "回数"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "試行回数"
    SendKeys "{right}", True
    ActiveCell.FormulaR1C1 = "平均"
    For n = 2 To n_max
     SendKeys "{down}", True
     For j = 1 To 3: SendKeys "{left}", True: Next
     ActiveCell.FormulaR1C1 = n
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = kaisuu(n)
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = shikoukaisuu_max
     SendKeys "{right}", True
     ActiveCell.FormulaR1C1 = kaisuu(n) / shikoukaisuu_max
    Next
    Range("A3").Select
End Sub




NO.610 '99 9/11水の流れ三平方の定理

第２８回数学的な応募問題

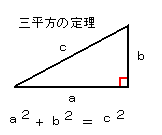
三平方の定理は、数学の中でも最も大切な定理の１つです。 この定理は直角三角形の３辺の長さの間に成り立つ単純で明快な関係を与えています。 その応用については、実際に起こりうるような身近な問題を今回は考えてみましょう。

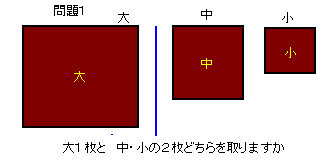
問題１：

図のような正方形のチョコレートが３枚ある。 このチョコレートを次のように２組に分ける。
大１枚のチョコレートと中・小のチョコレート２枚
このとき、どちらの組のチョコレートの方が量が多いか、 ３枚のチョコレートを配置するだけで調べてみることができる。 どのように配置すればよいか。ただし、チョコレートの厚さはすべて同じとする。

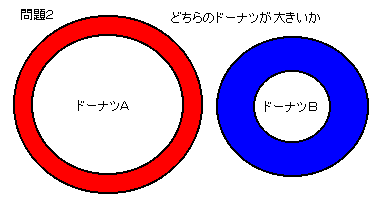
問題２：

図のような形の異なるドーナツ状のクッキー（どれも境界は同心円）が２個あります。 １本の糸を用いて、どちらのクッキーの量が多いか調べるには、 どうしたらよいでしょうか？ただし、クッキーの厚さはどちらも同じとする。

太郎さんは、授業で取り扱い、生徒にどちらを選ぶか考えさせたいと思っています。
＜出典：作って試して納得数学：監修秋山仁（数研出版）＞



NO.611 '99 9/13月の光オイラーの「無限解析入門（１）」（２９）

NO.540　オイラーの「無限解析入門（１）」（１６）にある 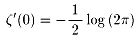を示せ、について


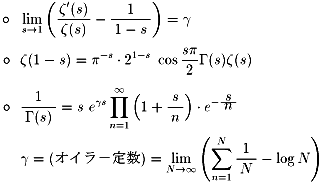
を用いて証明してください。



NO.612 '99 9/14Idaho Potatoハワイアン・イヤリング（１）

今月の問題　円の問題 を見て、次のような円の面積に関する問題を思い出しましたので、 紹介します。
これは、私のオリジナルではなく、ある数学者(誰かは思い出せない)から 聞いて知ったものです。

直径1の円に、直径1/2, 1/4, 1/8, ..., 1/(2n), ... の(無限個の)円が 同一の点で内接している図形を、「ハワイアン・イヤリング」といいます。
この図形において、
直径1の円と直径1/2の円にはさまれた領域、
直径1/4の円と直径1/8の円にはさまれた領域、
... というように、外側から「1つおきに」領域に色をつけます。
このとき、色のついた領域の面積を求めてください。

まぁ、すべての円が1点で接していることは本質的ではなく、 同心円でも同じことですけどね。
(ハワイアン・イヤリングは、それ自体位相的に興味深い性質を もっていることから、トポロジーの研究対象になっているのです。)





NO.613 '99 9/19Junkoハワイアン・イヤリング（２）

ハワイのイヤリングはこういう形をしているのでしょうか？　もちろん有限でしょうが・・・。
一番大きい円の半径を１とするとその面積はπです。
たとえば１番外側を赤、２番目を青と言う風に交互に色をつけていき、 赤の部分の面積をＲ、青の部分の面積をＢとします。
両者を足せば一番大きい円の面積になりますから、Ｒ＋Ｂ＝π
赤の部分を1/4倍すると青の部分に一致しますので、(1/4)Ｒ＝Ｂ
これより、Ｒ＝４／５π、Ｂ＝１／５πとなります。

円を内接させていくときに、直径を1/2ではなく、 一般にｐ(0＜p＜1)という比で作っていくとします。
先ほどと同様に、Ｒ＋Ｂ＝π
赤の部分をp２倍すると青の部分に一致しますので、p２Ｒ＝Ｂ
これより、Ｒ＝(1/1+p２)π、Ｂ＝(p２/1+p２)πとなります。





NO.614 '99 9/24水の流れ試験の採点

第２９回数学的な応募問題

太郎さんの学校では、２４日から定期考査が始まります。 数学の試験において、２０点満点の問題を５題出題しました。 各問題とも０点、５点、１０点、１５点、２０点のいずれかで全部を採点するつもりです。 次の問に答えよ。

問題１．
可能な採点方法は何通りあるか。

問題２．
少なくとも３問が正解で、あとは部分点の場合の採点方法は何通りあるか。

問題３．
総得点が８０点以上である採点方法は何通りあるか。

　

太郎さんは、採点を始める前に考えておきたいと思っています。



　
NO.615 '99 9/27水の流れオイラーの「無限解析入門（１）」（３０）

オイラーの無限解析入門（１）の第１５夜の始まり、始まり。

皆さん！お久しぶりです。９月２４日の中秋の名月を鑑賞されましたか。
いつ見ても、夜空に輝く美しい満月はいいですね。宇宙への夢を奏でてくれます。

さて、NO.542の第９夜の話をご存じですか。 もう一度、書きます。
オイラーは１７４０年の秋に、フランスの数学者フィリップ・ノードから、 「自然数を異なる自然数の和として表わす方法がいくるあるか？」という手紙を受け取りました。 これが、オイラーの興味を引きました。少し説明します。
例えば、ｎ＝６のとき、異なる自然数の和として、次の４通りがあります。
６，５＋１、４＋２，３＋２＋１　です。
６を構成している数字は１回だけしか使えません。 だから、異なっている数字なら、数字はいくつ使ってもよいです。
ここで、ある自然数ｎを異なる自然数の和で表わす方法をＡ（ｎ）とします。 つまり、Ａ（６）＝４　です。
次に、６を構成している数字が奇数だけになっている方法を考えて見ます。
５＋１，３＋３，３＋１＋１＋１，１＋１＋１＋１＋１＋１ の４通りです。
奇数という制限はありますが、同じ数字を繰り返して使ってもよいです。 ある自然数を奇数の和で表す方法をＢ（ｎ）とすれば、 Ｂ（６）＝４となります。
皆さん、Ａ（６）＝４　、Ｂ（６）＝４　が偶然でしょうか。

そして、NO.544の第１０夜を見て下さい。 当然ある関数の係数として表れてきます。これが、母関数です。
そこで、皆さん、次の関数を展開してくださいね。
当然係数に注目ください。 そして、この係数がどうして、数列｛Ａ（ｎ）｝なのかも考えてください。
Ｆ(ｘ)＝(１＋ｘ)(１＋ｘ２)(１＋ｘ３)(１＋ｘ４)・・・・・・
＝１＋ｘ＋ｘ２＋２ｘ３＋２ｘ４＋３ｘ５ ＋４ｘ６＋５ｘ７＋６ｘ８＋８ｘ９＋１０ｘ１０ ＋１２ｘ１１＋１５ｘ１２＋・・・・・・


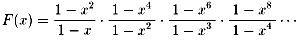
ところが、展開しないで、これを　(１＋ｘｎ)(１−ｘｎ)＝１−ｘ２ｎ を用いて書き変えてみます。



１−ｘｎ　はｎが偶数のものは約分されて消えて、ｎが奇数のものだけが分母に残ります。 よって、



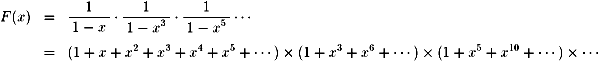
この式の持っている意味を説明します。

ここから、、「数学の宇宙」＜現代数学社＞のオイラーの９１ページから引用します。
例えば、ｘ５の係数は　ｘ５、ｘ３・ｘ２、ｘ５から得られます。
だから、ｘｎの項の数と、指数がすべて奇数ですから奇数の和として 　ｘ　と書き方法は同じです。
言い換えればこのことは、異なる自然数の和で表わす方法をＡ（ｎ）と 奇数の和で表す方法をＢ（ｎ）は正確に等しいことを示しています。
これが、オイラーが見つけた証明です。 自然数を分解することについて、微妙で曖昧だった真実を明確にしたこの論証は、 まさに傑作といわねばなりません。
そしてこれは、次のようなオイラー数学の典型的な正確を表しています。

１．オイラーは抽象的な記号を用いた式の扱いが素晴らしく巧みでした。 その能力はこの証明にもはっきり現れています。 よって彼は”どんな場合にも、最も偉大な記号の使い手”という評判を得ています。

２．オイラーの最も実り豊かな数学的戦略の１つは、同じ式を二種類の方法で書き表すことで、 その二つの式を等式化することによって力強い結論を引き出していくものです。 これがまさにその通りです。 また、読者の皆さんは、既に、「ゼーター関数ζ（２）物語」のときにも、 どこまでも異なる二つの見地から１つの目標を見出していく美しい論証で、 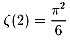を発見したことも良い例です。

３．彼の代数学に高度な操作や技術的に優れた技量を取ってみたとき、 そこに残るのは創意工夫の力です。これはもうただただ驚くほかありません。

この章の最後に、こんなことばが書いてありました。 

『誰よりも洞察力にあふれ、
　　　誰よりも影響力をもち、
　　　　　　誰よりも創造性豊かな数学者！
　　　　　　　　　それはスイスのレオナルド・オイラー！』

これで、まだ幾つかの課題を気にしつつ、第１５夜を閉じます。







E-mail 戻る