
Weekend Mathematics/コロキウム室/1999.10〜12/NO.76
| NO.663 | '99 11/17 | Junko | ロケットの性能(2) |
少なくとも1つが故障して打つ上げに失敗する確率は、
すべての部品に故障がない確率を1から引けばいいわけです。
「mathematica」で計算してみました。「Excel」でもOKですね。
問1:
1-(0.999)1000=0.6323045752
問2:
1-(0.999)10000=0.9999548266
問3:
1-(0.99999)100000=0.6321223982
問4:
1-(0.999999)100000=0.0951626272
問5:
1-(0.9999999)100000=0.0099501667
この結果から、精度0.999(スリ−ナイン)はおおあまということですね。
10万個の部品に対しては精度0.9999999(セブンナイン)でも失敗する確率が1%程度もあるわけです。

| NO.664 | '99 11/17 | kiyo | 大縄跳び (3) |
この問題は、ベーシック言語のFOR〜NEXT文の構造と同じですね。
水の流れさんの
「カタラン数のレポート」として、
歴史的経過を含めて詳細が報告されています。
Junko先生の一般式の他に色々表現があるようですがシンプル
なのは以下のものではないでしょうか。
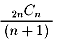

| NO.665 | '99 11/17 | Junko | 大縄跳び (4) |

Combination と言えば、パスカルの三角形です。
2nCn は、左図のように
パスカルの三角形において1段おきに中央に現れます。
これを順に (n+1) で割れば、カタラン数となるわけですね。
{1,2,5,14,42,132,429,1430,・・・}

| NO.666 | '99 11/18 | Junko | 大縄跳び (5) |
縄の左側を持つ人をL、右側を持つ人をRとします。
n個のLとn個のRを1列に並べることを考えます。
ただし縄が交差してはまずいわけですから、左から数えていった時に常にLの数がRの数より等しいか
大きくなくてはなりません。
そう考えると、NO.121 つり銭の問題(1)
と同じだということがわかります。
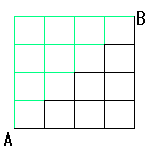 更に、NO.127 つり銭の問題(3)で、
「水の流れ」さんがおっしゃっているように、Lを「→」、Rを「↑」で表せば、
まさにこれを1列に並べることと同じです。
更に、NO.127 つり銭の問題(3)で、
「水の流れ」さんがおっしゃっているように、Lを「→」、Rを「↑」で表せば、
まさにこれを1列に並べることと同じです。
もちろん、左から数えて常に「→」の数が「↑」の数より等しいか
大きくなくてはなりません。
それは左図(n=5)で、AからBへ黒い道だけを通って行く行き方を数えればよいということになります。

| NO.667 | '99 11/19 | ch3cooh | ロケットの性能(3) |
ロケットの問題では、単純に部品点数と信頼性から
不良率を計算していますね?
実際の製品の製造では、全体としての不良率を削減
するためにさまざまな工夫が行われています。
その手段として、良く使用されているのがモジュール
単位による製造です。
自動車も、構成部品点数の多い製品ですが、製造時の
コスト削減や、機能向上のために部品のモジュール化が
進んでいます。
これは、車の構成要素である"エンジン"や"ブレーキ"
等の単位でいったん組み立て、そのモジュールに対して
動作試験を行うことで、不良品を落とすというものです。
(これにより、不良率を下げることが可能)
ただし、製品の不良は、製造時の不良のみでなく、"初期不良"
や、"寿命"というものもあります。
"初期不良"というのは、多くは製造時に軽微な不良が
発生しているものの、検査で検出できないものです。
これに対する対処として、"エージング"が行われます。
"エージング"は、その装置に対して負荷動作をある一定
期間行わせるものです。
(これにより、初期不良品の市場における発生を抑制する)
ロケットのエンジンなどでも、"予備燃焼試験"等で"エージング"
を行い、故障率を下げています。
(それでも、過酷な動作が要求されるために、難しい技術
であることは確かですが・・・)
・・・ 物の設計・製造をしているため、弁解のような文章を
書いてしまいましたが、これは"数学"とはあまり関係ないような・・・
(注: 工学的には、"品質管理工学"という分野が存在していて、
不良品の発生によるロスコストと、検査に必要とするコストを
統計処理によりバランスを取り、生産性を上げることも行われ
ている。
ちなみに、これは第2次世界大戦で、USAが飛行機の不良率を
下げるために研究され、発達した。
戦後は、USAの産業界ではあまり重視されず、日本の産業界で
発達し、"品質"の高さで物が売れるようになった。
'80後半からは多大なダメージを受けたUSAが逆輸入し、ユーザに
受け入れてもらえるような品質になっている。)

| NO.668 | '99 11/20 | 水の流れ | 大縄跳び (6) |

カタラン数はパスカル三角形の中で、
F(n)=2nCn-2nCn-1という観点から、
偶数段の中央値を n+1で割らなくても、中央値をから隣の数字を引くと生まれてきます。

| NO.669 | '99 11/21 | 水の流れ | 橋を渡る(1) |
太郎さんの勤務している学校に行くには、大きな川(揖斐川)を渡らなければなりません。
こんな問題を考えました。
この川にはn個の橋が架かっています。
太郎さんは自転車で後戻りせず、自転車の轍に交差がないように、
すべての橋を一度渡りきってみたくなりました。
川上から順に、橋に自然数をつけて、1番から渡り始めて、
最後に渡り終える橋は何番でも良いとします。
次の問に答えてください。
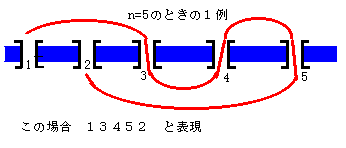
問題1:
n=2,n=3,n=4,n=5,n=6のときの轍の数は何通りですか。
(ただし、n=1のときは、便宜的に1通りとすます。)
参考図のように、数字の順番にて、轍を表現して、何通りか答えてください。
問題2:
一般の場合の轍の数をnで表すことは、現在分かっていないようです。
何か漸化式とか、ここまで発見したとかレポートみたいで結構ですので、知らせてください。
太郎さんは、「数学100の発見(数学史を彩る発見と挑戦のドラマ):数学セミナー編集部」
<日本評論社>を読んでいて、考えました。

| NO.670 | '99 11/23 | Junko | 橋を渡る(2) |
問題1:
 の1通り。
の1通り。
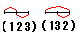 の2通り。
の2通り。
 の4通り。
の4通り。
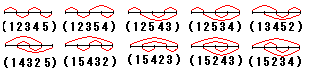 の10通り。
の10通り。
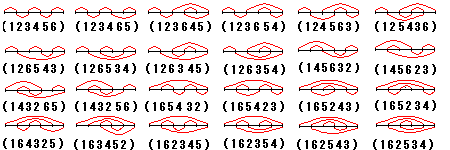 の24通り。
の24通り。
ここまでは地道に数えましたが、私には漸化式も規則性も見えてきません・・・。

 E-mail
E-mail
 戻る
戻る