
Weekend Mathematics/コロキウム室/1999.10〜12/NO.77
| NO.671 | '99 12/1 | 水の流れ | タクシーの相乗り(1) |
一部訂正(12/1,19:00)
「太郎さんは、昨夜、割り勘の約束で3人がタクシーに相乗りしました。
次郎さんは全行程の16分の3の所で降り、2分の1の所で三郎さんも降りた。
最後に、太郎さんは4320円払ったが、次郎さんや三郎さんにいくら請求したらよいか
考えました。」
「割り勘といったって、3等分というわけにもいかないし、
乗った距離は、3:8:16だから、・・・」
と悩んでしまいました。
一体、合理的に、次郎さん、三郎さんにいくら請求するのがよいか考えてください。

| NO.672 | '99 12/2 | sambaGREEN | タクシーの相乗り(2) |
こういった問題の「公平」,「平等」は捉え方がむずかしいですが,
次のように考えるのも1つの方法でしょう。
16分の3(810円分)は3人で乗っていたので,
ひとりあたり 810円÷3=270
16分の5(1350円分)は2人で乗っていたので,
ひとりあたり 1350円÷2=675円
16分の8(2160円分)は1人で乗っていたので,
ひとりあたり 2160円÷1=2160円
したがって,次郎・・・270円,三郎・・・270+675=945円,
太郎さん・・・270+675+2160=3105円

| NO.673 | '99 12/2 | 浜田 明巳 | タクシーの相乗り(3) |
最初の3/16の所までは,3人の割り勘で太郎さん,次郎さん,三郎さんが
1/16ずつ負担します.
次に1/2の所まで,つまり次の5/16の行程は,
2人の割り勘で太郎さん,三郎さんが5/32ずつ負担します.
最後の所まで,つまり次の1/2の行程は,1人の割り勘で太郎さんが1/2負担します.
つまり太郎さんは1/16+5/32+1/2=23/32の負担,
次郎さんは1/16+5/32=7/32の負担,
三郎さんは1/16の負担となります.
故に太郎さんは次郎さんに4320円×7/32=945円を,
三郎さんに4320円×1/16=270円をそれぞれ請求すればよいでしょう.

| NO.674 | '99 12/2 | ch3cooh | タクシーの相乗り(4) |
単純な距離と、その間の利益を受けている人数から計算すると・・・
行程の距離/人数 となるでしょう。
そこで、
次郎さん : 3/16 × 1/3= 1/16
三郎さん : 上の分は計算清算されたとして
1/2 × 1/2= 1/4
となるでしょう。
ただ、実質的な計算をする場合は、行程がまったくの直線状で
他の人の家に寄ることによって、伸びないことと、
乗り降りの時間、タクシーのスピードの増減が無いこと(飛び降り?!!)
が前提となります。
タクシーの料金体系が2時曲線的に増加すること等を考えに入れる等 を考えると、書いてある通り 3/16, 1/2 でも良いかと思います。 (ただし、次郎さんはもう少し減らしてあげても良いかもしれない。)
どちらにしても、対人関係なども考えて、そこそこ納得の行く値にすると
良いでしょう。

| NO.675 | '99 12/3 | ふじけん | タクシーの相乗り(5) |
まず、初乗り料金をa円とします。
この金額は距離に従わないのでみんなで3等分します。
残りの金額4320−a円をタクシー代が距離に比例すると考えると
(実際はどうだかわかりませんが・・・。)
NO.673の浜田 明巳さんと同じ考え方で
太郎さんは4320−a円の内23/32の負担
次郎さんは4320−a円の内1/16の負担
三郎さんは4320−a円の内7/32の負担
となります。
したがって、太郎さんは
次郎さんに(4320−a)/16+a/3円
三郎さんに(4320−a)×7/32+a/3円
を請求すべきだと思います。
ただ、こんな細かい所まで請求するとケチだと思われそうですね。

| NO.676 | '99 12/3 | Junko | タクシーの相乗り(6) |

皆さんの考え方を図にするとこういうことでしょうか?
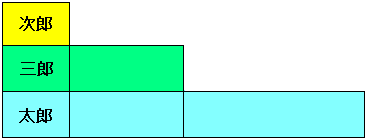
こういう考え方もあっていいですよね?
つまり乗った距離が 3:8:16 ですから、この比で分配するということです。
こう考えると、
次郎さん:4320×(3/27)=480
三郎さん:4320×(8/27)=1280
太郎さん:4320×(16/27)=2560
の負担ということになります。

| NO.677 | '99 12/4 | Idaho Potato | まきの問題 |
今月の「まきの問題」はなかなかおもしろいですね。
登場人物は日本人らしいのに、通貨単位がロシアだったり…(笑)
でも、私が思うに、これは「数理的」な問題というよりは、
むしろ「社会的」な問題ではないでしょうか?
水の流れさんの「タクシーの相乗り」問題も同じですが、 このような分配問題は、どんな分け方をしても、 それで当事者どうしが納得すればかまわないわけで、 その意味で「客観的に正しい分け方」というのは、 必ずしも一意的には定まらないといえます。
「まきの問題」
について言えば、どのような分配が妥当であると考えるかは、
共用ストーブをめぐる二人の社会的関係に依存して定まる性質のもので、
問題文には、二人の社会的関係について、妥当な分配方法を考えるために
十分な情報が含まれていないと思うのです。
このことを明確にするために、「まきの問題」に、
次のような問題を追加して考えてみます。
次の日、三木さんと五木さんの共通の友人である八木さんが遊びに来て、
お土産に8本のまきを持ってきてくれました。
二人は、これをどのように分配すればよいでしょうか。
この問題と、木無君からもらった8コペイカの分配問題を、
「本質的に同じ」と考えるか、それとも「異なる」と考えるかによって、
答え方はまるで変わってくると思います。
私は、これらは「本質的に同じ」ような気がしてなりません。
そういうわけで、近いうちに、上述の「社会的見地」からの解答を
お送りしたいと思います。
それが出題者の意図した解答だとは、とても思えないのですが…(^^;)

| NO.678 | '99 12/5 | 水の流れ | ドアーの破損数(1) |
太郎さんは、生徒と共に修学旅行に行きます。
ホテル泊まってシングルルームで休んでいたとき、
「先生大変です。すぐ来てください。」と言う生徒の声に夢中で飛び出して、
失敗しことがあります。
実は、自動ロックのドアーでして、鍵を持たずに飛び出したのです。
幸いフロントに言って、合い鍵を使って、助かったことがあります。
さて、あるいたずら好きな子供が、幾つかの部屋の別々な鍵を、
適当に各室に1個ずつ入れ、自動ロックのドアーを閉めてしまいました。
あいにく、合い鍵がないので、ドアーをこわさなければなりません。
その部屋に別の部屋の鍵があれば、そこはこわさずに開くことができます。
全部の部屋を開けるのに、
こわさなければならないドアーの個数の期待値を求めなさい。
問題1:
まず、部屋の数をnとして、n=1,2,3,4の場合を考えてください。
問題2:
部屋の数をnとして、n=5のときの場合を考えてください。
<発展>
一般のn部屋の場合、こわさなければならないドアーの個数の期待値を求めたいのですが、
太郎さんは、正直なところ、まだ、解答に至っていません。
解けた人は教えてください。

| NO.679 | '99 12/7 | Junko | ドアーの破損数(2) |
部屋の数をnとするとき、こわさなければならないドアーの個数の期待値を f(n) とします。
問題1:
地道に数えてみました。
A室、B室、C室、D室・・・として、その部屋の中にある鍵、
そしてその際にこわすドア−数を表にしました。
鍵がない状態でこわすドア−の優先順位はABCDとします。
(これは結果に影響しないので。)
| A室 | こわすドアー数 |
|---|---|
| A | 1 |
| A室 | B室 | こわすドアー数 |
|---|---|---|
| A | B | 2 |
| B | A | 1 |
| A室 | B室 | C室 | こわすドアー数 |
|---|---|---|---|
| A | B | C | 3 |
| A | C | B | 2 |
| B | A | C | 2 |
| B | C | A | 1 |
| C | A | B | 1 |
| C | B | A | 2 |
| A室 | B室 | C室 | D室 | こわすドアー数 |
|---|---|---|---|---|
| A | B | C | D | 4 |
| A | B | D | C | 3 |
| A | C | B | D | 3 |
| A | C | D | B | 2 |
| A | D | B | C | 2 |
| A | D | C | B | 3 |
| B | A | C | D | 3 |
| B | A | D | C | 2 |
| B | C | A | D | 2 |
| B | C | D | A | 1 |
| B | D | A | C | 1 |
| B | D | C | A | 2 |
| C | A | B | D | 2 |
| C | A | D | B | 1 |
| C | B | A | D | 3 |
| C | B | D | A | 2 |
| C | D | A | B | 2 |
| C | D | B | A | 1 |
| D | A | B | C | 1 |
| D | A | C | B | 2 |
| D | B | A | C | 2 |
| D | B | C | A | 3 |
| D | C | A | B | 1 |
| D | C | B | A | 2 |
問題2:
上述のn=4の時の表を見ながら、何か規則性はないものかと考えました。
4!=24の組み合わせのうち、A室にどこの鍵があるか(A or B or C or D)によって規則性が見えてきます。
A室をこわして入ったとき、そこのあった鍵がAだとすると、
次にB室のドア−をこわすことになり、そこから先はn=3の時と同じになります。
しかし、最初にA室のドア−をこわしていますから、こわすドア−数はそれぞれ+1となります。
一方A室をこわして入ったとき、そこのあった鍵がBだとします。(C、Dも同様)
その鍵を持ってB室をあけることになります。
この時点でB室をA室と読み替えればn=3のときと同じになります。
従って、f(4)を次のようにして求めることもできます。
f(4)={(11+6)+11×3}/4!=50/24=25/12
同じように、
f(5)={(50+24)+50×4}/5!=274/120=137/60
発展:
一般にも同じことがいえますから、
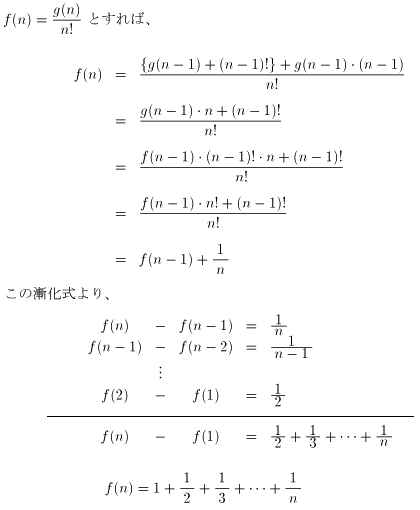

| NO.680 | '99 12/12 | 水の流れ | 13の倍数 |
太郎さんは、ある整数がどんな倍数であるかを見分けるのに、ときどき使っています。
それは、4桁から6桁の整数のときに、13の倍数である判定方法があります。
千位以上の部分と百位以下の部分の差を作る。それが13の倍数になれば
元の整数は13の倍数である。
例えば、53092のとき、
千位以上は53,百位以下は092で、その差は92−53=39であるから、
元の数字は13の倍数である。
どうして、いつもこんな判定ができるか考えてください。

 E-mail
E-mail
 戻る
戻る