Weekend Mathematics/コロキウム室/テーマ別/43.ガウスの発散定理の応用
| NO.1318 | 2002.11.5. | DDT | ガウスの発散定理の応用(1) |
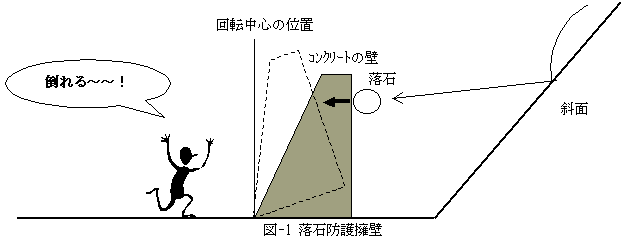
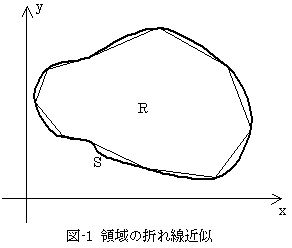
最近、落石防護擁壁の転倒計算に関わりました。落石防護擁壁とは、図-1に示すようなコンクリートの壁のことで、斜面を転げ落ちて来た落石に衝突されても、倒れないだけの自重を持たなければなりません。

どれほどの自重(重さ)があれば良いのでしょうか?。斜面を転げ落ちて来る落石は、運動エネルギーを持ちます。もし落石の運動エネルギーがそのまま全部、擁壁に伝わるなら、面倒はありません。擁壁重心の位置エネルギーを落石の運動エネルギーに等しいとおいて、擁壁重心の変位を計算し、それが回転中心の位置を越えなければOKです。しかし現実のエネルギー伝達には、常にエネルギー損失が憑き物(?)で、全てが擁壁に伝わるわけではありません。エネルギー損失の定量理論は現在に到っても難しい問題で、一般的な傾向を述べる概論めいたものはあっても、個々の特殊事情までも考慮して使用できるような、完璧な理論化はなされていません。いきおい実験ということになります。ところがエネルギーは直接測定できる量ではありません。
ではいったい何が測定できるのかというと、例えば、コンクリート擁壁に鉄球をぶつけるような実験では、鉄球に加速度計を仕込んでおきます。加速度計は、鉄球が擁壁に衝突する際に生じる、鉄球の加速度を記録します。その衝突加速度波形に鉄球の質量をかければ、衝突の際に擁壁から鉄球に作用した衝撃力波形が得られます。これは鉄球から擁壁に作用した衝撃力でもあるはずです。要するに直接測れるのは、力の時間変動の様子だけです。衝撃力波形の記録を数値的に時間積分すれば、衝突時に鉄球から擁壁に伝達された運動量(力積)が出ます。この運動量によって擁壁は動き出すのですから、伝達運動量に見合う擁壁の運動速度を定めれば、運動エネルギーの形で鉄球から擁壁へ伝達されるエネルギーを計算できます。この伝達エネルギーは、衝突の際に生じる力の実測から得られたものなので、衝突時に起きたエネルギー損失を全て含む、正しい伝達エネルギーであるはずです。
すいません。やっと本題です。愚痴っぽく言うと、伝達運動量から擁壁の運動速度を算出するために、剛体回転の運動方程式を解く破目に陥りました。剛体回転の運動方程式には、次の3つの定数が必要です。
質量M,重心位置(x0,y0,z0),固有慣性モーメントI0(重心回りの慣性モーメント)
で、密度が一様な2次元剛体の場合は、それぞれ、
面積A,重心位置(x0,y0),固有極断面2次モーメントIp
の計算に帰着されます。計算式は以下となります。
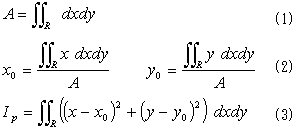
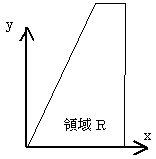
対象とする積分領域Rは、右図にように比較的簡単なものです。まず(1)の面積は台形公式で簡単に計算できますが、(2)になると、もう単純な公式はすぐには出てきません。それでも構造力学公式集やデザインデータブックを検索すると、何とか使う気になる程度の公式は出てきました。でも(3)については公式すらありません。
しかたないので、右図のような座標系を入れ、x,yに関する2重積分を使って計算しましたが、かなり面倒な微積分計算となり(高校レベルです)、久しぶりにやったので3時間もかかってしまい、その上結果に自信が持てないという有様でした。
じつは最初に述べた実験では、せっかくだからということで、加速度計のほかに歪み計(擁壁の変形を測定する)やレーザー変位計(擁壁の変位を測定する)を沢山盛り込み、実験は相当に高額なものでした。もちろん実験資金は、発注者の金です。「こりゃ、ちゃんとした結果を出せないと首がとぶぞ」と皆で薄笑いを浮かべる始末。(3)の結果の検算に迫られました。
 (1)~(3)は、ガウスの発散定理を利用して計算できます。これが思いのほか便利だったので、報告します。しかも、どんなにいびつな領域に対しても、それを詳しく折れ線近似しておけば、十分な精度で答えを出せます。任意多角形に対してはもちろん正解を与え、Cadの利用を前提に考えれば、折れ線近似をCad上でスケッチしただけで、折れ点の座標データをファイル出力できるので、プログラム化(自動化)にはもってこいです。
(1)~(3)は、ガウスの発散定理を利用して計算できます。これが思いのほか便利だったので、報告します。しかも、どんなにいびつな領域に対しても、それを詳しく折れ線近似しておけば、十分な精度で答えを出せます。任意多角形に対してはもちろん正解を与え、Cadの利用を前提に考えれば、折れ線近似をCad上でスケッチしただけで、折れ点の座標データをファイル出力できるので、プログラム化(自動化)にはもってこいです。
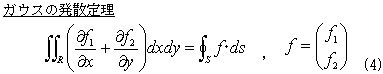
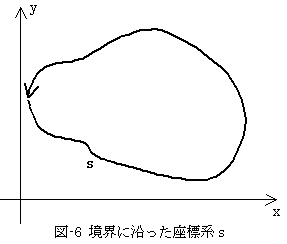
Rは積分領域,Sはその境界,dsは境界の接線線素ベクトルdnと右回りに直行する外法線線素ベクトル,
一周積分の方向は、もちろん左回り.
式(4)において、
f=(x/2,y/2)TでAが,f=(x2/4,xy/2)Tでx0が,f=(xy/2,y2/4)Tでy0が,f=((x-x0)3/3,(y-y0)3/3)TでIpが出ます。

| NO.1320 | 2002.11.11. | DDT | ガウスの発散定理の応用(2) |
ガウスの発散定理について説明します。
1.2重積分について
2重積分とは、図-1のように平面領域Rがあり、Rに含まれる点(x,y)において2変数関数f(x,y)が定義されているとき、
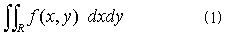
のように表わされるもので、関数f(x,y)をxで積分した後、yで積分せよ、という意味です。
最も簡単な例として、f(x,y)が変数(x,y)について定数1である場合を考えます。
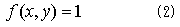
なので、2重積分(1)は、
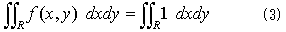
となります。式(3)は、領域Rの面積を与えます。どうしてかというと、まずyを一つ固定して、定数1をxで積分するので、
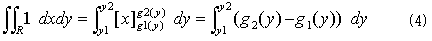
となりますが、g1(y)とg2(y)とは図-1に示したように、領域Rの境界Sをx方向の高さに関して上下に分けて、縦線①~②までの境界Sの部分をx=g2(y),縦線②~①の部分をx=g1(y)と表わしています。縦線①と②に直交する点線は、x軸に平行な境界Sの接線を表わします。g2(y)-g1(y)は 明らかに、固定したyに応じた領域Rの横幅です。
次にg1(y)とg2(y)の不定積分をG1(y),G2(y)とした場合、 (4)の最右辺では最初に固定したyを、今度は動かして積分するので、
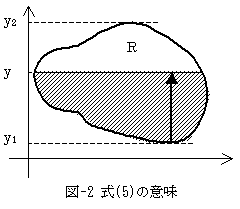
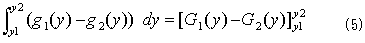
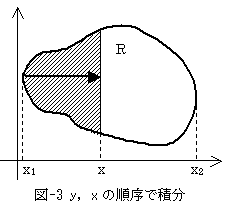
となり、確かに領域Rの面積です。何故なら式(5)は、各yに対して変化する領域Rの横幅を、yの下限から上限まで順番に積算していったものだからです(図-2)。同じ結果は、yで積分した後、xで積分しても得られるはずです。図-3は、各xに対して変化する領域Rの縦幅を、xの下限から上限まで順番に積算していったことを意味します。
よって、
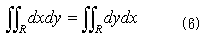
です。うるさい事さえ言わなければ、もっと一般に任意の関数f(x,y)に関して、
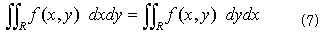
も成り立ちます。横に積算してから縦に積算するか、それともその逆かの違いしかないからです。式(7)の左辺を、図-2方式で2重積分すれば、
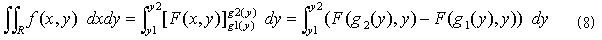
となります。
2.ガウスの曲面論[1]
多様体の概念の基礎を与えたのは、恐らくリーマンです。こんにち多様体の一分野となった、微分幾何学や微分多様体を出発させたのは、しかしガウスです。ガウスの曲面論は疑いもなく、リーマンの多様体の概念の出発点にもなりました。幾重にも広がった量として、その就任公演で多様体のイメージを初めて述べたリーマンですが、就任公演は当時、大学への就職試験のようなものでした。その面接官であったガウスは、リーマンに完全な満点評価を付けました。多様体の概念は、ガウスの曲面論をより一般的に具体化するものだったからです。
多様体の重大な理論的成果の一つに、図形はその内部性質のみによって、完全に自己を記述できる、というのがあります。これはある図形を、その図形を含むより高次元の空間から、外から見なくても、図形に貼りついた視点で図形を詳細に調べれば、外から見た図形の姿を再現できるという意味です。考えようによっては、ものすごい結果だと思います。例をあげれば一般相対性理論です。
我々は3次元空間に住んでいますが、その3次元空間を詳細に調べれば、一般相対性理論が言うように宇宙は曲がった4次元時空だとわかる、という意味です。実際、4次元の中の3次元宇宙の曲率を測る実験の数々が、現在進行形で考案されている現実があります。これを3次元の中の2次元曲面論の形で最初に提出したのは、ガウスでした。

曲面を外から見た姿を曲面内部から知る方法は、私の狭い理解範囲内で言えば、曲面に沿った座標系を曲面に入れることによって実現されます。曲面に沿った座標系とは、図-4の右図のようなものです。対比として、平面に対する平面に沿った座標系を書いてあります。図-4においては、平面の格子点が、そのまま曲面の格子点に対応していると想像して下さい。余りにも面倒なので図-4の座標格子では省略してしまいましたが、曲面に沿った座標格子の格子点間隔は一定でなくても良いのです。曲面の格子点間隔を平面格子に対応付けて、どのように自然に与えれば良いかは、ガウスの理論に述べられています。そして、曲面の格子点間隔の変化を丹念に追跡することで、曲面の曲がり方がわかり、ひいては曲面を外から見た姿も再現でき、かつ格子点間隔の測定は曲面内部の性質だけから決定できるはずだ、というのがガウスの曲面論です。だって格子点間隔は、曲面に沿って測るだけですから。逆に言えば、曲面と仮定して測った格子点間隔がどこでも一定なら、図-5に示したように、どんなに傾いていても、どんなに遠い場所にあろうと、どんなに大きさが違っても、平面は平面で平らだということが内的性質のみを使って、もってまわったやり方ではありますが、ともかく一目瞭然となります。ここで、図形の傾きや位置やスケールは、外的性質であって、図形の形とは無関係です。
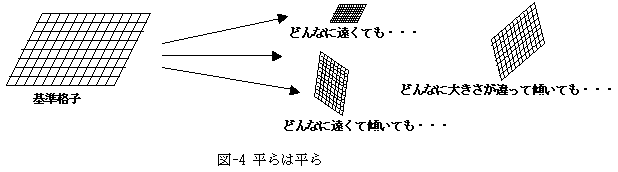
現在ではガウスの曲面論のアイデアは、3次元CadのRuled Surface(線織面)や、Meshed Surfaceの計算法として、コンピュータ内で実現されています。もしガウスがいなかったら、CGも造れなかったかもしれません。
3.内部座標系の威力
もう一度、式(8)と図-1を、式(9)と図-5として並べて書きます。
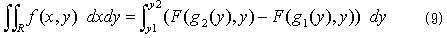
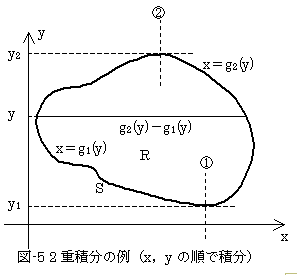
式(9)の右辺において、F(x,y)のxは、g1(y)とg2(y)におきかわっています。g1(y),g2(y)は、二つ合わせて式(9)左辺の積分領域Rの境界Sを構成します。ということは、式(9)の右辺のFは、一見2変数関数の形をしていますが、実質は境界Sに束縛された、1次元の(1変数の)関数です。それを、FS(y)と書きます。
FS(y)のyに関する積分値は、関数x=g1(y)とx=g2(y)の形で決まるので、じつは境界Sの形で決まります。
よって式(9)は本来、
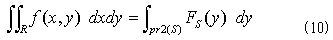
のように書かれるべきです。ここで右辺の積分範囲pr2(S)は、境界曲線Sのy軸への正射影で、区間[y1,y2]を表わします。ところで曲線は曲面の一種と考えることができます。境界曲線Sの形とは、まさに曲線Sに固有な内部的性質です。式(9)の値が、ということは式(10)の値が境界Sの形で決まるということは、言い直せば、積分値が境界Sの内部的性質から定まることを意味します。領域Rは境界Sの形をその定義とするので、領域Rに固有な、形という内部性質だけから、積分値が定まるといっても同じです。これが式(10)の意味です。この見方は事の本質を捉えていると思います。それは面積の例を考えれば明らかです。
事の本質が上記の通りなら、その通りに式を変更すべきです。2.で述べたように、曲面に沿った座標系とは、座標系自身が載る曲面の形すら再現するほど強力なものでした。そして式(10)の積分値は、積分領域の形から定まるものです。積分を実行する座標系として、境界に沿った座標系sを採用します。以後内部座標と呼びます。
次式は正しい式ではありません。
話を簡潔にするための模式図と考えて下さい。式(9)より、
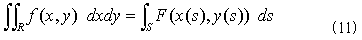
と大変簡潔な形になります。式(11)と(9)を比べてみると、何故あんなに式(9)が不細工になったのかが理解できます。境界Sを外部座標x-yで表わしていたからです。まさに境界Sの形を外から観察し、x=g1(y),x=g2(y)と境界の形を表わす情報を外から与える必要に迫られました。式(10)においても、積分区間pr2(S)=[y1,y2]は、境界Sに固有な表現ではなく、やはり不満足なものです。[y1,y2]をy軸への正射影とする曲線は無数にあるからです。その責任は、外部座標yを積分パラメータとし、それを偏重したからです。式(11)では、それらの情報の全てが、内部座標系sの中に含まれています。よって式を不細工にした責任は外部座標にある!。お前が悪い!!。
とはいえ計算を実行する人間は、境界内部には住んでいません。問題をスケッチするために、最初は何らかの外部座標に頼らざるえません。理屈の上では、領域Rも境界Sも最初からその内部座標で表わしておけば、外部座標不要で済ませられますが、上の理由からそれは実用的ではありません。だから式(11)のように、外部座標を介在させる書き方が、最もバランスの良いやり方と思えますが、そうすると外部座標と内部座標とを結ぶ変換則が必要になります。Frenet-Serretの公式がそれですが、それを用いてx(s)やy(s)を求めようとすると、初等関数で積分できなくなったりしてなかなか辛い目に会います。だから式(9)のタイプも多用されるわけです。
4.ガウスの発散定理
長い前ふりでした。すいません。理屈の上では、2重積分の実行は、境界の内部座標で実行すべきだということになりましたが、その方法にはほとんど実用性がないのも事実です。しかし次の形の2重積分、
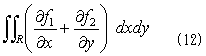
に関しては、内部座標での積分の実行を行うと、結果をきれいなベクトル形式にまとめられます。外部座標と内部座標の変換もFrenet-Serretの公式を使わずに、その関係をスケッチするだけで済みます。式(12)は、ガウスの発散公式(発散定理)の一部で、その名の示すとおり、彼はこのタイプの積分を考える機会が多かったはずです。そしてガウスは、内部座標の威力に、恐らく世界で初めて気づいた人です。
ガウスの発散定理
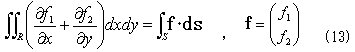
Rは積分領域,Sはその境界,dsはSの外法線線素ベクトル,・は内積を表わし、線積分の方向は左回り.
[説明]
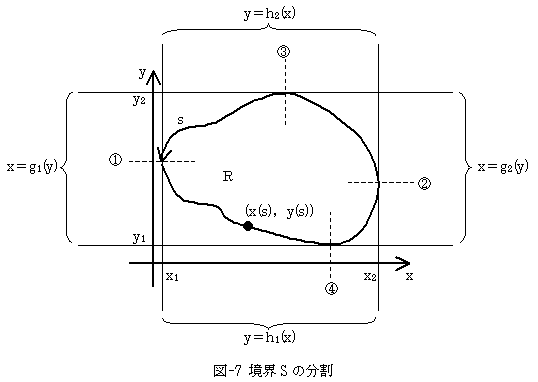
まず問題を定式化するために、表式がいかに不細工になろうとも、外部座標を利用します。問題の定式化に関しては、それが唯一の現実的手段だからです。そのためにRの境界Sを、4つの部分に分けます(図-7)。
図-7で、境界Sの①→②の部分をy=h1(x),②→①の部分をy=h2(x)で、③→④の部分をx=g1(y),④→③の部分をx=g2(y)で表わします。
次に式(13)の、
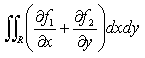
の部分ですが、ガウスでなくてもというか、ガウスでさえも、とりあえずは第1項はxで、第2項はyで積分したくなったに違いない思われます。1.で述べたように、x,yの順序で積分しても、y,xの順序で積分しても、2重積分の積分結果に違いはありません。f1=f1(x,y),f2=f2(x,y)と堂々と書くことにして、
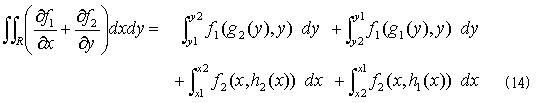
です。ただし後で便利に書き換えられるように、積分区間の上下限の順序を適宜変えて、積分記号の前の符号を揃えています。内部座標sでの積分を実行したいので、式(14)をsで書き換えることを考えます。
上式右辺上段のf1(g2(y),y)は、f1(x,y)の(x,y)が曲線Sに束縛されたために、(x,y)=(g2(y),y)とパラメータ表示された状態だと読めますが、Sは、(x,y)=(g1(y),y)または(x,y)=(g2(y),y)と表わされる点全体のことなので、右辺上段の積分を実行するために、yをy1からy2まで動かせば、曲線Sに束縛された点(x,y)は、自動的に曲線S上の全ての点を通ります。しかも同じ点は2度と通りません。よって曲線Sの内部座標sと点(x,y)との間に関数関係が成立し、(x,y)=(x(s),y(s))という記述が可能です。下段のf2の(x,y)=(x,h1(x)),(x,h2(x))についても同様で、(x,y)=(x(s),y(s))の記述が可能です。そこで内部座標sによるパラメータ表現を用いれば、式(14)は、
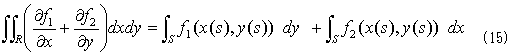
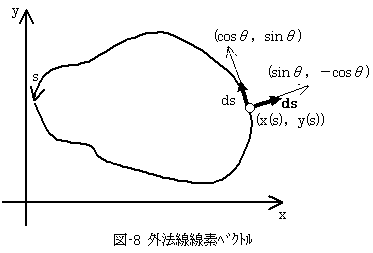
と書けてしまいます。このときsの原点は、S上であればどこでもOKです。どこに原点をおいても結果は変わらないのは、積分の一般的性質です。この段階で、外部座標(x,y)と内部座標sとの関係をスケッチします。
式(15)において、sへの書き換え作業として残っているのは、dx,dyをsで表わすことだけです。
図-8に示すように、S上の一点(x(s),y(s))での単位接線ベクトルを(cosθ,sinθ)とすれば、接線ベクトルは線素をdsとして、
(ds cosθ,ds sinθ) (16)
となります。これのx,y軸への正射影が-dxとdyなので、
dx=-ds cosθ
dy= ds sinθ (17)
です。dxに負符号がつくのは、図-8のdsがsに載って動いたときの正射影の方向と、式(14)の積分方向を比較するとわかります。
式(17)を(15)右辺に代入すれば、
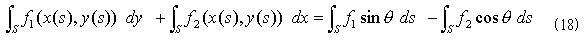
を得ます。図-8に示したように、単位外法線ベクトルは(sinθ,-cosθ)なので外法線線素ベクトルを、
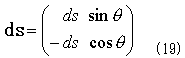
で導入し、f1とf2をまとめて、
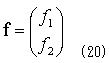
と書くことにすれば、式(18)の右辺の積分記号内は、f・dsとなり、
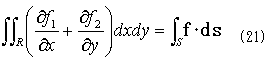
が得られます。
5.発散公式の実用性
式(13)または(21)の計算を内部座標で行う必要は全くありません。まず領域Rが任意多角形の場合は、隣り合った角点の(x,y)座標から、辺上の座標値をたやすく補間できるので、f1(x,y)やf2(x,y)の関数値は、その座標値を代入することで即座に出ます。線素ベクトルdsの方向についても、隣り合った角点を結ぶ矢線ベクトルの方向から簡単に計算できます。そして線素の大きさdsは、多くの場合、矢線ベクトルの長さで代用すれば十分です。Sが任意の曲線の場合は、解析的計算は不可能なケースがほとんどなので、Sを細かく折れ線近似し、任意多角形の場合と同様に扱います。
参考文献
[1]多様体,萩上紘一,共立講座 21世紀の数学6,共立出版1997

| NO.1333 | 2002.11.25. | DDT | ガウスの発散定理の応用(3) |
ガウスの発散公式を利用した、任意多角形の面積,重心,慣性モーメントの計算法です。
1.面積
例えば右図の領域R(滑らかな太線)の面積を計算する手順です。Rの境界Sの表式がわかっている場合でも、それを折れ線近似して(R内部の細い実線として)扱ったほうが、計算が速くて便利だったりするので、以後任意多角形の場合のみ扱います。もちろん図-1は、もう数倍細かく近似したほうが良いです。
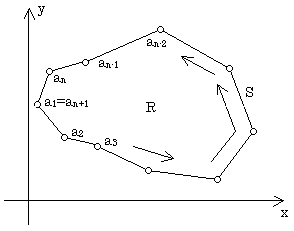 図-2の任意多角形に対して、その角点を、左回りの順番にa1,a2,・・・,anとします。a1は、どこから始めようとOKです。また出発点a1は1周して元に戻った時、aiの添数iが、nから1に突然ジャンプしないように、a1=an+1と二重化しておくと便利です。
図-2の任意多角形に対して、その角点を、左回りの順番にa1,a2,・・・,anとします。a1は、どこから始めようとOKです。また出発点a1は1周して元に戻った時、aiの添数iが、nから1に突然ジャンプしないように、a1=an+1と二重化しておくと便利です。
図-2の任意多角形Rの面積に関する通常の考えでは、Rの境界Sをy方向の高さに関して2つの関数、y=h1(x)とy=h2(x)に分け、その差(h2(x)-h1(x))をxで積分することによって計算するか、または多角形領域Rを三角形分割して、部分三角形の面積の合計として算出します。しかしこれらの方法では、面積は形から決まるという至極当然の事実が、直截には使われていません。
面積Aは、NO.1320で述べたように、
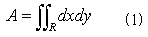
で計算できます。一方ガウスの発散公式(発散定理)は、
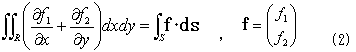
でした。式(1),(2)の意味は申し訳ないですがNO.1320を見てください。式(2)の右辺の線積分は、積分領域Rの境界Sなので、左辺の2重積分が境界曲線Sの形から直接決まることを示します。よって、もし式(1)の右辺の2重積分が(2)の左辺に等しいなら、面積Aが境界曲線Sの形から直接決まることになります。式(1)の右辺=式(2)の左辺とは、
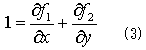
を意味します。そこで(3)を成り立たせる2変数関数f1(x,y)とf2(x,y)を探します。(3)を満たせばf1とf2は何でも良いので、
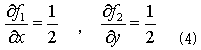
とします。ここから、
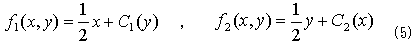
がただちに出ます。ここでC1とC2は、y,xに関する1回微分可能な任意の関数です。再び(3)さえ満たせば良いことから、C1=C2=0でもOKなので、
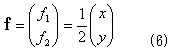
と決めます。明らかに(6)の決め方には、任意性がありますが、ここでは(x,y)について対称なものを選びました。面積という量は、座標系の取り方によって癖があってはいけないので、たとえ結果は同じであっても、(x,y)について対称な表式を選択するのが、妥当と思えます。
fの形が決まったので、図-2で定義した多角形の角点aiの座標から、(2)の右辺を算出する計算にかかります。角点aiの座標は多角形の形を定めるので、この情報だけから面積を計算できるはずです。
角点aiからai+1への辺上では、
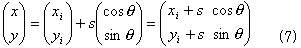
と書けます。ここでai=(xi,yi)T,ai+1=(xi+1,yi+1)T,sは、 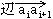 に沿った座標系,(cosθ,sinθ)Tは、
に沿った座標系,(cosθ,sinθ)Tは、 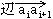 の単位接線ベクトルで明らかに、
の単位接線ベクトルで明らかに、
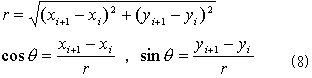
で計算できます。外法線線素ベクトルは、(8)のθを右にπ/2回した方向なので、
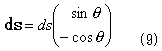
となり、(7),(8),(9)を式(2)右辺に代入すれば、 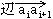 では、
では、
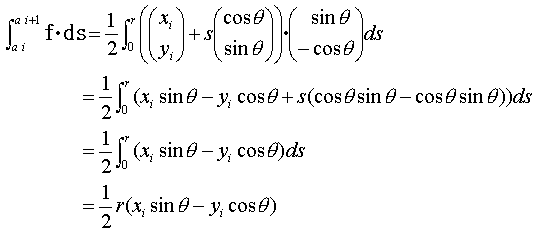
となり、式(8)を考慮すれば、
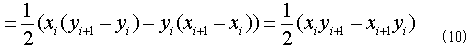
となります。これが多角形の1辺上での式(2)右辺の値なので、式(2)右辺全体としては(境界S全体では)、これらを寄せ集めて、
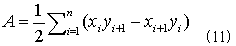
(後で気づきましたが、原点を中心に多角形領域を3角形分割した場合の、部分三角形の符号付面積の合計です。・・・当たり前の結果でした・・・)
が得られます。
2.重心位置
任意の領域Rの重心座標(x0,y0)は、NO.1320より、
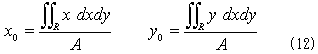
で計算できます。面積Aは、すでに1.でやっつけているので、右辺分子が計算できればOKです。x方向の重心座標x0についての計算は、1.と同様に、
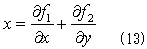
となるf1(x,y)とf2(x,y)を探します。ここでも(x,y)に関して対称になるように、
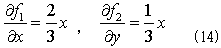
を採用します。式(4)から(5)を得たのと同じ発想で、
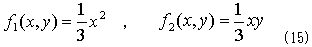
で十分です。よって、
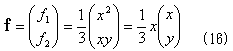
となりますが、式(16)のどこが(x,y)について対称なのでしょう?。まずこれは、x方向の重心位置を計算する式なので、x方向への偏りがなければなければなりません。それが式(16)最右辺のベクトルの係数xです。そしてベクトルの中身は1.のfに等しく、(x,y) について同じ式で構成されるので対称です。式(7)と(9)より、
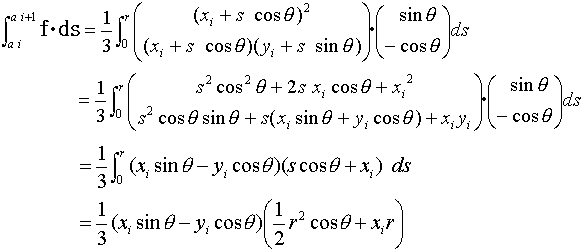
であり、式(8)を考慮すると、
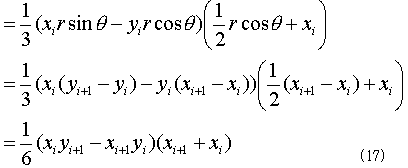
従って、
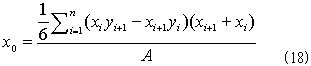
(さっきの部分三角形の重心の、面積の重み付き平均です。・・・知ってる人には、当たり前の結果でした・・・)
となります。y0に関しては、最初の座標系を右にπ/2回転させれば、古い座標系のy軸を新しいx'軸とでき、x軸 → -y'軸,y軸 → x'軸の関係があるので、x → -y,y → xの交換を行えば、
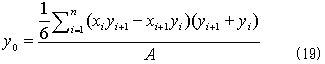
となります。
3.慣性モーメント
慣性モーメントはふつう、重心まわりで計算されますが、任意の点(x0,y0)を中心としても同じです。
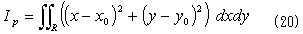
式(20)は、極断面2次モーメントといわれる一種の断面係数で、物体の面密度一定なら、これに面密度ρをかけたものが慣性モーメントです。回転中心(x0,y0)を原点とする座標系に移ります。
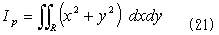
x2+y2は最初から、(x,y)について対称性を持っているので、
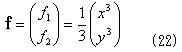
と決めます。
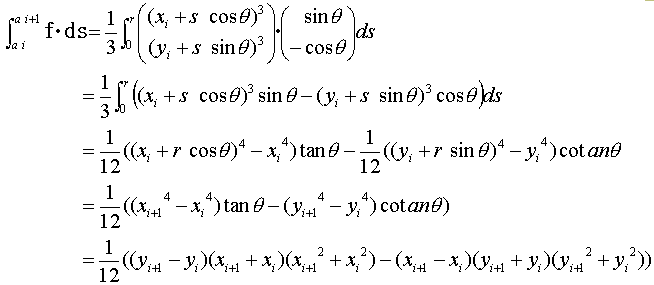
なので、
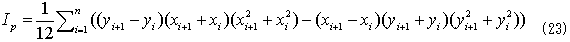
です。cosθ=0の場合や、sinθ=0の場合の場合分けをやっていないので少々反則気味ですが、場合分けしてやっても結果は変わりません。さらにこの(x,y)は、Ipの回転中心を原点とした座標系です。式(23)も幾何学的に解釈できますが、複雑になります。工学屋の発想としては、領域境界の座標を押さえれば各種量を計算できるということだけが重要です。ここでは都合良く工学屋に徹します。

| NO.1336 | 2002.12.7. | かつ | ガウスの発散定理の応用(4) |
DDTさんが曲面論についてお話をしていたので多少補足してみたいと思います。
曲面の状態を考えるときに外的なことは必要ないのはそのとおりですが、もう
ちょっと詳しく説明してみたいと思います。
曲面に座標系を作る事というのは多様体の定義です。曲面上に格子点を作り局所
的に平面座標に落として考ようと考えるからです。
そこで、曲面は曲がったりしているわけですから局所的に格子点を作るだけでは
何も理解できません。そこで曲がり具合というのを調べることにしました。それ
がガウス曲率と呼ばれるものです。はじめガウス曲率は高さ(平面座標に落とし
たとしても高さが必要、これが外的性質)が必要だとしたのです。しかしなが
ら、このガウス曲率を調べると外的性質(高さ)を必要としない局所座標内の接
ベクトルによって表現することができました。これにはガウスも驚いたそうで
す。なのでこれは「ガウスの驚異の定理」とも呼ばれています。これによって、
たとえばこの地球が球状だということをスペースシャトルや人工衛星などを使わ
なくても地球上にいて理解できるのです。
なんだか文章で書いてしまったのでわかりにくくてすみません。
ちょっと解釈がDDTさんと違うかもしれませんがそのところはご容赦ください。

| NO.1342 | 2003.1.5. | DDT | ガウスの発散定理の応用(5) |
ガウスの発散定理の応用(2)は、全て理解もしていないくせに、けっこう知ったかぶりして書きました。「ガウスの驚異の定理」は、かつさんのおっしゃる通り、曲率についてのお話です。職業柄「測量」が身近にあるもので、直接測れない曲率を、直接測れる「距離の変化」におきかえてしましました(言われてみれば、曲率を距離の変化におきかえて良いんだろうか?)。いずれにしろ正確な姿を伝えて頂きありがとうございます。
「驚異の定理」に気づいたガウスが、図形は図形自身で形を決められる事にも気づいて、累次積分の発散形式への定式化に向かったのだとしたら・・・そんな事を考えていたら、なにかわくわくして知ったかぶりしてでも書きたくなった、というのが本音です。

 戻る
戻る