�P�S�T�D�Q�O�O�X�N�̖��
[��]�ł����Ȃ��ő�̐�����\���܂��B���Ƃ��A[�Q�D�T]���Q�A[�O�D�Q]���O�ł��B
�����P����Q�O�O�X�܂ł̐����̒l���Ƃ�Ƃ��A
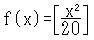 �@�@
�@�@
�́A���ʂ�̒l���Ƃ肦�܂����B
�@�� �����Ȃ��ő�̐�����\��[��]���K�E�X�L���ƌĂт܂��B
���̏o�T
�L���t�n�C���x�����w���w�ɒ���
�Z���I�����s�b�N�ψ���ďC
�u�k�Ѓu���[�o�b�N�X
2002�N�t�@�C�i����� ����
�����Ɖ��
�E����1
�i�y���l�|���F�J�̖��j
���̏������l�Ƒ傫�Ȓl�������ĕ\�ɂ܂Ƃ߂�ƁA�ȉ��̗l�ɂȂ�B
| x | x2/20 | [x2/20] | ������ | ������ |
|---|---|---|---|---|
| 1 | 0.05 | 0 | �@ | �@ �@ |
| 2 | 0.2 | 0 | �@ | �@ �@ |
| 3 | 0.45 | 0 | �@ | �@ �@ |
| 4 | 0.8 | 0 | �@ | �@ |
| 5 | 1.25 | 1 | �@ | �@ |
| 6 | 1.8 | 1 | �@ | �@ |
| 7 | 2.45 | 2 | �@ | �@ |
| 8 | 3.2 | 3 | �@ | �@ |
| 9 | 4.05 | 4 | �@ | �@ |
| 10 | 5 | 5 | �@ | �@ |
| 11 | 6.05 | 6 | �@ | �@ |
| 12 | 7.2 | 7 | �@ | �@ |
| 13 | 8.45 | 8 | �@ | �@ |
| 14 | 9.8 | 9 | �@ | �@ |
| 15 | 11.25 | 11 | 10 | 1 |
| 16 | 12.8 | 12 | 13 | 1 |
| 17 | 14.45 | 14 | 15 | 1 |
| 18 | 16.2 | 16 | 17 | 1 |
| 19 | 18.05 | 18 | 19 | 1 |
| 20 | 20 | 20 | 21 | 1 |
| 21 | 22.05 | 22 | 23 | 1 |
| 22 | 24.2 | 24 | 25 | 1 |
| 23 | 26.45 | 26 | 27 | 1 |
| 24 | 28.8 | 28 | 29,30 | 2 |
| 25 | 31.25 | 31 | 32 | 1 |
| 26 | 33.8 | 33 | 34,35 | 2 |
| 27 | 36.45 | 36 | 37,38 | 2 |
| 28 | 39.2 | 39 | 40,41 | 2 |
| 29 | 42.05 | 42 | 43,44 | 2 |
| 30 | 45 | 45 | 46,47 | 2 |
| 31 | 48.05 | 48 | 49,50 | 2 |
| 32 | 51.2 | 51 | 52,53 | 2 |
| 33 | 54.45 | 54 | 55,56 | 2 |
| 34 | 57.8 | 57 | 58,59,60 | 3 |
| 35 | 61.25 | 61 | 62,63 | 2 |
| 36 | 64.8 | 64 | 65,66,67 | 3 |
| 37 | 68.45 | 68 | 69,70,71 | 3 |
| 38 | 72.2 | 72 | 73,74,75 | 3 |
| 39 | 76.05 | 76 | 77,78,79 | 3 |
| 40 | 80 | 80 | 81,82,83 | 3 |
| 41 | 84.05 | 84 | 85,86,87 | 3 |
| 42 | 88.2 | 88 | 89,90,91 | 3 |
| 43 | 92.45 | 92 | 93,94,95 | 3 |
| 44 | 96.8 | 96 | 97,98,99,100 | 4 |
| 45 | 101.25 | 101 | 102,103,104 | 3 |
| 46 | 105.8 | 105 | 106,107,108,109 | 4 |
| 47 | 110.45 | 110 | 111,112,113,114 | 4 |
| �@ | �@ | �@ | �@ | �@ |
| 2003 | 200600.45 | 200600 | �@ | 199 |
| 2004 | 200800.8 | 200800 | �@ | 200 |
| 2005 | 201001.25 | 201001 | �@ | 199 |
| 2006 | 201201.8 | 201201 | �@ | 200 |
| 2007 | 201402.45 | 201402 | �@ | 200 |
| 2008 | 201603.2 | 201603 | �@ | 200 |
| 2009 | 201804.05 | 201804 | �@ | �@ |
�����A�������̐��Ɍ��炸�A1�`199�܂ł͓������̔��������K��10�ӏ��Â��݂���B �A���A������200��4�ӏ��ł���B�����āA
�i1+2+3+�E�E�E�E�E+198+199�j�~10+200�~4��199800�ƂȂ�B
���̐���201804��������ƁA2004�ƂȂ邪�A0�����݂���̂ň�����A���߂���̂�2005�ł���B
�E����2
�i�y���l�|���F�l�c�����j
�G�N�Z���̃}�N���ʼn����܂����D����2005�ʂ�ł��D2009�ʂ�̓��ɂȂ�悤�Ȗ�肾�Ƃ���ɗǂ��������ȁH
Option Explicit
Const MAX As Long = 1000000
Sub Macro1()
Sheets("Sheet1").Select
Cells(1, 1).Value = 0
Dim x As Long
Dim xx As Long
Dim a(MAX) As Long
Dim kotae As Long
Dim j As Long
For j = 1 To MAX
a(j) = 0
Next j
For x = 1 To 2009
xx = Int(x * x / 20)
a(xx) = 1
Cells(x, 2).Value = x
Cells(x, 3).Value = xx
Range("C" & x).Select
Next x
kotae = 0
For j = 0 To MAX
kotae = kotae + a(j)
Next j
Cells(1, 1).Value = kotae
Range("A1").Select
End Sub
--------------------------------------------------------------------------------
Power up the Internet with
�E����3
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�����@�Q�O�O�T�ł��B
���P�D
F(1)=INT(1`2/20)=0 F(2)=INT(2`2/20)=0 F(3)=INT(3`2/20)=0 F(4)=INT(4`2/20)=0
F(5)=INT(5`2/20)=1 F(6)=INT(6`2/20)=1�@F(7)=INT(7`2/20)=2�@F(8)=INT(8`2/20)=3
��L����F(7)�`F(2009)�܂ł͂��ꂼ��قȂ鐮���ł��鎖��������܂��B
�]���āi�Q�O�O�X�|�V�j�{�P���Q�O�O�R
F(1)F(6)�܂ł̂Q�����Z����2003+2=2005�ł��B
���Q�D
CASIO�@FX -870P�y��FX-890P�Ńv���O��������萔���܂����B
�@�P�O, PRINT �h2009�l���@�m�@�����_�C�h ; C=1: D=0 �@�Q�O, IF INKEY$= �h �h THEN 20 �@�R�O, FOR X=1 TO 2009 �@�S�O, E=INT(X^2/20) : PRINT �h * �h ; �@�T�O, IF E>D THEN C=C+1 �@�U�O, D=E �@�V�O, NEXT �@X �@�W�O, CLS : BEEP : BEEP : PRINT�h�Z�C�X�E�@�m�@�J�Y�n�h ;C; �h�R �f�X�h �@�X�O, IF INKEY$= �h �h THEN 90 �@�P�O�O, GOTO 10
��L�̃v���O�����̐���
�Q�O�s�Ńv���O�����͒�~���Ă��܂��̂ʼn����̃L�[�������ƂQ�O�s�`�V�O�s�̂Q�O�O�X��̌v�Z�����܂��B
�W�O�s��CLS�ŕ\����ʂ�������2���BEEP���Ōv�Z���ʂ��o�����Ƃ������Ă���܂��B
�����ĂX�O�s�Ńv���O�����͒�~���Ă��܂��̂ʼn����̃L�[�������ƂP�O�s�ɖ߂�܂��A
�v�Z���͂S�O�s�̃v���O�����łP��̌v�Z�Ł����\������܂��̂łQ�O�O�X���A�����ĕ\������v�Z���ł��邱�Ƃ�������܂��B
CASIO FX-870P�Ōv������ƃX�^�[�g���ĂU���P�W�b�Ō��ʂQ�O�O�T�ƕ\������܂��B
Office2007�̃G�N�Z���̃��[�U�[�t�H�[���ō��܂����B�������u���ɕ\������܂��B
�e�L�X�g�{�b�N�X�ɐ���������ƑO�̓����������܂��B�E���ɃR�[�h�������Ă���܂��B

�E����4
�i�y���l�|���F�̂�����j
f(1)=f(2)=f(3)=f(4)=0
f(5)=f(6)=1
f(7)=2
f(8)=3
f(9)=4
f(10)=5
(x+1)2-x2=2x+1 ������
x��10 �̎��A(x+1)2��x2+20
�����x��10�̎��Af(x)��f(x+1)�������l���Ƃ邱�Ƃ͂Ȃ�
2009-4=2005�i�����j
�E����5
�i�y���l�|���Fkohji�j
x��9�̂Ƃ�
(x+1)2-x2=2x+1��20
�]����[x2/20]�̒l��x�͈�Έ�ɑΉ�����B�܂�
[12/20]=0,[22/20]=0,[32/20]=0,[42/20]=0,[52/20]=1,
[62/20]=1,[72/20]=2,[82/20]=3,[92/20]=4,[102/20]=5
�Ȃ̂ŁAf(x)�͑S����2009-4=2005�ʂ����肤��B
�E����6
�i�y���l�|���F�I���W�j
(�T�j�P�������P�O�̂Ƃ�
�@�i�@�j�P�������S�̂Ƃ�
�@�@�@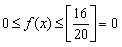
�@�@�@�]���ā@���i���j���O
�@�i�A�j�����T�A�U�̂Ƃ��@�@���i���j���P
�@�i�B�j�V�������P�O�̂Ƃ�
�@�@�@���i�V�j���Q�A���i�W�j���R�A���i�X�j���S�A���i10�j���T
�i�U�j�����P�O�̂Ƃ�
�@�i���{�P�j�Q�|���Q���Q���{�P���Q�P���
�@���i���{�P�j�����i���j�F���i���{�P�j�A���i���j�͎��R��
�@���߂鐔�́A�@�Q�O�O�X�@�\�i�R�{�P�j���Q�O�O�T
�@���@�Q�O�O�T
�E����7
�i�y���l�|���F�]�ʔ����j
��=1,2,3, �c10�ɑ��āA���i���j�����߂�ƈȉ��̒ʂ�B
| �� | [���Q/20] | ���i���j |
|---|---|---|
| 1 | �m1/20�n | 0 |
| 2 | �m4/20�n | 0 |
| 3 | �m9/20�n | 0 |
| 4 | �m16/20�n | 0 |
| 5 | �m25/20�n | 1 |
| 6 | �m36/20�n | 1 |
| 7 | �m49/20�n | 2 |
| 8 | �m64/20�n | 3 |
| 9 | �m81/20�n | 4 |
| 10 | �m100/20�n | 5 |
���āA��̘A�����鐮����,�@���{�P�ɑ��āA���i���j���قȂ鐮�� ����邽�߂ɂ́A
�@�@�@���i���{�P�j�|���i���j���m�i���{�P�j�Q�^�Q�O�n�|�m���Q�^�Q�O�n���P�@
�m���Q�{�Q���{�P�n���m���Q�{�Q�O�n�@�ƕό`����
�Q���{�P���Q�O�@����@�����X�D�T
����āA���������P�O�ɑ��āA���i���j�͑S�ĈقȂ鐮�������
��=1,2,3, �c9 �ɑ��āA5�ʂ�
x=10,�c,2009�ɑ��āA2000�ʂ�
�v�@2005�ʂ� �i��)
�E����8
�i�y���l�|���F�X���[�N�}���j
(10*k+a)2=100k2+20ak+a2
�Ȃ̂ŁA�A�A
[x2/20]=5k2+ak+[a2/20]
0��a��4�E�E�Ea2��20�E�E�E0
52=25�E�E�E1
62=36�E�E�E1
72=49�E�E�E2
82=64�E�E�E3
92=81�E�E�E4
k ��1�ȏ�Ȃ炷�ׂĈقȂ�B
�܂�Ax ��10�ȏ�Ȃ炷�ׂĈقȂ�B
2009-9=2000
1�`9 �܂ł́A�ォ��A5��ނȂ̂ŁA
2000+5=2005 �ʂ�
�ł����̂��� ��
�E����9
�i�y���l�|���F�O�p��K�j
x��10 �̂Ƃ�
�@{( x�{1)2�|x2}/20��( 2x�{1)/20��( 2�E10�{1)/20��1
������
x��10 �̂Ƃ��@[ ( x�{1)2/20 ]��[ x2/20 ]
����āCx �� 10 �ȏ�̐����̂Ƃ� [ x2/20 ] �͈قȂ�l���Ƃ�B
x��1�C2�C3�C4 �̂Ƃ� [ x2/20 ]��0
x��5�C6 �̂Ƃ��@�@�@ [ x2/20 ]��1
x��7 �̂Ƃ� �@�@�@�@�@[ x2/20 ]��2
x��8 �̂Ƃ� �@�@�@�@�@[ x2/20 ]��3
x��9 �̂Ƃ� �@�@�@�@�@[ x2/20 ]��4
x��10 �̂Ƃ��@�@�@�@�@[ x2/20 ]��5
�ł��邩��Cx �� 1 ���� 2009 �܂ł̐����l���Ƃ�Ƃ��C[ x2/20 ]�@�́C2005 �ʂ� �̒l���Ƃ�B
�E����10
�i�y���l�|���F���q�̗Y�L�j
���i���j�@�̒l�͕K�������ł���B
�i����P�j���@���P����P�O�܂ł̐����̒l���Ƃ�Ƃ��A
�@�@�@���i���j�@�͂U�ʂ�̒l���Ƃ�B
�i����Q�j�����P�O�@�̏ꍇ�A���i���j�@���@���i���{�P�j�@�ł���B
�@�@�@����ƁA���@���P�P����Q�O�O�X�܂ł̐����̒l���Ƃ�Ƃ��A
�@�@�@���i���j�@�͂P�X�X�X�ʂ�̒l���Ƃ邱�ƂɂȂ�B
����āA�����P����Q�O�O�X�܂ł̐����̒l���Ƃ�Ƃ��A���i���j�́A�Q�O�O�T�ʂ�̒l���Ƃ肦��B
�i����P�j�̏ؖ�
���i�P�j�@���m�P���Q�O�n���O
���i�T�j�@���m�T�~�T���Q�O�n���m�Q�T���Q�O�n���P
���i�V�j�@���m�V�~�V���Q�O�n���m�S�X���Q�O�n���Q
���i�W�j�@���m�W�~�W���Q�O�n���m�U�S���Q�O�n���R
���i�X�j�@���m�X�~�X���Q�O�n���m�W�P���Q�O�n���S
���i�P�O�j�@���m�P�O�~�P�O���Q�O�n���m�P�O�O���Q�O�n���T
���i�P�P�j�@���m�P�P�~�P�P���Q�O�n���m�P�Q�P���Q�O�n���U
��L���A
���@���P����P�O�܂ł̐����̒l���Ƃ�Ƃ��A���i���j�@�͂U�ʂ�̒l���Ƃ�B
�ؖ��I���
�i����Q�j�̏ؖ�
�P���炁�Q�܂ł̐����ŁA�Q�O�̔{���ł��鐮���̌����A���i���j�Ɠ������B
���i���j�����Q�ƒ�`����B
���@���@�P�O�̏ꍇ�A
���i���{�P�j�|���i���j�|�P
�@���i���{�P�j�Q�|�i���j�Q�|�P
�@���@���Q�{�Q���{�P�|�i���j�Q�|�P
�@���@�Q���{�P�|�P
�@���@�Q�O
�ł��邩��A���i���j���Ă��i���{�P�j�ȉ��̐����̂����A�Q�O�̔{���ł��鐮��
�����Ȃ��Ƃ��P�͊܂܂��B
�ؖ��I���
�E����11
�i�y���l�|���Fteki�j
�����@�@�Q�O�O�T�ʂ�
�ŏ��͐ݒ肪�Q�O�O�X�܂łȂ̂ŁA���傦�`�I�Ǝv���܂������A�P�P�܂�
�v�Z��������Ƃ킩���āA�ق��Ƃ��܂����B
�Ȃ��A�P�P�܂ł��Ƃ����ƁA���Q�|�i���|�P)�Q���Q���|�P�@�Ȃ̂ŁA����ȏ�
�́A�O�̐��Ƃ̍����P���邽�߁A�^���͑S�ĈقȂ鐔�ƂȂ邩��ł��B
���ۂɂP�P�܂ł́A�^�����O�C�O�C�O�C�O�C�P�C�P�C�Q�C�R�C�S�C�T�C�U�@�ƂȂ�A�V��ނ̐�������܂��B
�ŁA�Q�O�O�X�|�P�P�{�V���Q�O�O�T�ʂ�@���Ă킯�ł��B
�E����12
�i�y���l�|���F����܁j
���߂Ɂ@��1, x2��10 �̂Ƃ��A ��1����2 �Ȃ�A���i��1�j�����i��2�j �������܂��B
x1����2 �Ȃ̂ŁAx1��x2�Ƃ��܂��B
��12�|��22 �� (x1�{x2)(x1�|x2) �� 20(x1�|x2) �� 20
����āA�@�@x12 /20 ���@x22/20�{1
�]���āA�@�mx12 /20�n ���@�mx22/20�n
�����A�@f(x1) �� f(x2) �����藧���܂��B
���̂��Ƃ���A�� ��10����2009�܂ł̂Q�O�O�O�̒l���Ƃ�A���i���j�͂Q�O�O�O�̈قȂ�l���Ƃ�܂��B
����Af(1)��f(2)��f(3)��f(4)��0,�@f(5)��f(6)��1,�@f(7)��2,�@f(8)��3,�@f(9)��4,�@f(10)��5�@�ł�����A
�� ���P����X�܂ł̂Ƃ��́Af(��)�͂S�ȉ��̈قȂ�T�̒l���Ƃ�A
�� ���P�O�ȏ�̂Ƃ��́Af(��)�͂T�ȏ�̂Q�O�O�O�̈قȂ�l���Ƃ邱�ƂɂȂ�܂��B
�ȏ�̂��Ƃ���A��(��)�́A�قȂ�Q�O�O�T�̒l���Ƃ�܂��B�E�E�E�E�E�E�E�i���j
�E����13
�i�y���l�|���Fhaya�j
���145 2009�N�̖�� �̉��� 2005 �ł��B
�y�������z
�ׂ荇���������������l�ɂȂ����Ƃ���ƁA
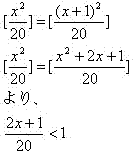
�@�@�@x �� 9.5
�]���āA�������� 1�`8 �܂ł͈̔͂̐����̏d���ׂď��O����悢�B
���ہA
| x | f(x) |
|---|---|
| 1 | 0 |
| 2 | 0 |
| 3 | 0 |
| 4 | 0 |
| 5 | 1 |
| 6 | 1 |
| 7 | 2 |
| 8 | 3 |
�ƂȂ�A�d����4�Ȃ̂ŁA��蓾��l�̐��� 2009 - 4 = 2005
�E����14
�i�y���l�|���FT_Tatekawa�j
�܂��Cx=k �̏ꍇ�� x=k+1 �̏ꍇ���r���܂��D
(k+1)2 = k2 + (2 k+1)
�ł��D���� (2k+1) > 20 �Ȃ�C
[(k+1)2/20] �� [k2/20] �͈قȂ�l�����܂��D
2k+1 > 20 �ƂȂ鐮�� k �� 10 �ł��D����� x �� 10 �ȏ�
2009 �ȉ��͈̔͂ł́C[x2/20] �͑S�ĈقȂ�l�ƂȂ�܂��D
x �� 1 ���� 9 �܂ł̎��́C�e�X�� 2 ���
1, 4, 9, 16, 25, 36, 49, 64, 81, 100
�Ȃ̂ŁC[x2/20] ��
0, 0, 0, 0, 1, 1, 2, 3, 4, 5
�� 6 �ʂ�ł��D������
(2009-10) + 6 = 2005 �ʂ�
�E����15
�i�y���l�|���F�o���^�����l�j
�����F�Q�O�O�T
������ƌ��A�Ƃ����ɂ������ł����A�w���P���������ɐV���Ȑ��ƂȂ邩�ǂ�
�����l����Ηǂ������̊ȒP�ȐV�t�T�[�r�X���B
�w���P�`�S�ł͂��i���j���O
�w���T�`�U�͂��i���j���P
�w���V�łQ�A�w���W�łR
�w���X�łS�C�w���P�O�łT
�w���P�P�ȏ�ł́A�w���P�������Ƃ����̐��͂Q�O�ȏ㑝������̂�
���i���j�͕K���P�ȏ㑝���A�V�������ƂȂ�B
���Ԃ��Ă��鐔�͂S�Ȃ̂łQ�O�O�X�|�S���Q�O�O�T
�E����16
�i�y���l�|���F��ӂ����̂炢��������j
��(��)��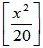
(���{�P)�Q�|���Q���Q���{�P���Q�O���
�����P�O�̐�����
��(��)����(���{�P)�ƂȂ�܂��B
������A�����P�O�܂łׂĂ݂܂��B
| x | ���Q | 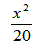
| 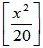
| �Ȃ��� |
|---|---|---|---|---|
| 1 | 1 | 0.05 | 0 | �@ |
| 2 | 4 | 0.20 | 0 | 1 |
| 3 | 9 | 0.45 | 0 | 2 |
| 4 | 16 | 0.80 | 0 | 3 |
| 5 | 25 | 1.25 | 1 | �@ |
| 6 | 36 | 1.80 | 1 | 4 |
| 7 | 49 | 2.45 | 2 | �@ |
| 8 | 64 | 3.20 | 3 | �@ |
| 9 | 81 | 4.05 | 4 | �@ |
| 10 | 100 | 5.00 | 5 | �@ |
�ȏォ��
��(��)�̎�肦��l�̌���
�Q�O�O�X�|�S���Q�O�O�T�ʂ�B
������
| teki | �o���^�����l | �X���[�N�}�� |
| �̂����� | �]�ʔ��� | ��ӂ����̂炢�������� |
| �l�c���� | �J�̖� | haya |
| ��̂������� | ���q�̗Y�L | �I���W |
| T_Tatekawa | ����� | �O�p��K |
| kohji |
�R�����g
�Ƃ肠����������������m�F���āA10���炢�܂ł����Ό��������܂��ˁB
f(x)�̂Ƃ肤��l��m�肽���̂ŁA�d�Ȃ肾�����ׂ�悢�킯�ł��B
�����āA10���炢�܂Œ��ׂĂ���A��������ŏ[���Ƃ����킯�ł��B
 top
top