���180�@�R�ƂV�̖��
2001 �ȉ��̐��̐����̂����A��̈ʂ��R�܂��͂V�ł�����̂��ׂĂ̐ς��w�Ƃ���B �w�̏\�̈ʂ����߂Ă��������B
���̏o�T
���w�I�����s�b�N
���{�]�_��
��21����{���w�I�����s�b�N�\�I(2011�N)
��
�`�������ɂ��Љ�܂��`
�E����1
�i�y���l�|���FT_Tatekawa�j
�\�̈ʂɂ͕S�̈ʁC��̈ʂ��܂ފ|���Z�͉e����^���Ȃ��̂ŁC�����̉��ɒ��ڂ���D
�܂�C1����100�܂ł��l����D�����ň�̈ʂ� 3 �܂��� 7 �ł�����̂�
�@�@3, 13, 23,..., 93
�@�@7, 17, 27,..., 97
�ł���D�\�̈ʂƈ�̈ʂ����C�\�̈ʂ��O�ɂȂ�Ȃ��|���Z�̕������o��
�����l����D
�\�̈ʂ�1��C��̈ʂ�19��|�����|���Z�ƁC��̈ʂ������|�����|���Z�����ɂȂ�D
�@�@(0+10+20+...+90) * 39 * 710+ (0+10+20+...+90) * 310 * 79
+ 310 * 710
�@= 450* 39 * 79 * (3+7) + 2110
�ƂȂ�C�Ō�� 2110 �������\�̈ʂɉe�����y�ڂ��D
�@�@2110 = (20+1)10 = A * 100 + 10 x 20 x 19 + 110
= 100 A + 200 + 1
������A�͎��R���D
����āC1����100�܂łň�̈ʂ� 3 �܂��� 7 �ł�����̂̐ς̉�2���� 01 �ɂȂ�D
2001�ȉ��̐��̐����ŁC��̈ʂ� 3 �܂��� 7 �ł�����̂̑S�Ă̐ς�
��2���� "01" �� 20 ��Ȃ̂ŁC��͂� "01" �ɂȂ�D
����� X �̏\�̈ʂ� 0 �ł���D
�E����2
�i�y���l�|���F�̂�����j
X=3�E7�E13�E17�E23�E27�E�@�E�E�E�E�E�E�@�E1983�E1987�E1993�E1997
�@3�E7��21
�@13�E17��221
�@23�E27��621
�@�E�E�E�E�E�E�E�E�E�E
�@1983�E1987��3940221
�@1993�E1997��3980021
�i�P�jX�̉�2�������߂�̂ɕK�v�Ȃ̂͊e�X�ɂ��Ẳ�2���ł���
�i�Q�j�e�X�ɂ��ĉ�2����21�ł���
�@�@�@�i10a+3)(10a+7)=100a2+10a(3+7)+21=100(a2+a)+21
����ā@21200 �̉�2�������߂���ꂪX�̉�2���ƂȂ�
�@211�̉�2����21
�@212�̉�2����41
�@213�̉�2����61
�@214�̉�2����81
�@215�̉�2����01
�@216�̉�2����21
�@�E�E�E�E�E�E�E�E�E�E�E�E�E�E
�܂�A21m�̉�2����
�@�@m=5n�@ �̎� 01
�@�@m=5n+1 �̎� 21
�@�@m=5n+2 �̎� 41
�@�@m=5n+3 �̎� 61
�@�@m=5n+4 �̎� 81
200=5n ������21200 �̉�2����01 �����X�̏\�̈ʂ�0
�� 3+7=10 ���|�C���g�ł��傤���H
�����N��2011�N������u2011�ȉ��v�Ƃ������ɂ��Ă��悩�����̂ł͂Ȃ����Ǝv���܂����B
�E����3
�i�y���l�|���Fhaya�j
���F X�̏\�̈ʂ� 0 �ł�
�y�������z
���̑Ώۂ� 1 ���� 2001 �܂ł̐��̐����ł����A����10�̈ʂ̐��l�����߂���Ȃ̂ŁA��2���ɒ��ڂ��Ă�悢�B
1�̈ʂ�3�܂���7�̐�����2���ȉ��̐����́A
�@�@3, 7, 13, 17, 23, �c, 93, 97
�ł����A������傫�Ȑ�����10�̌����傫�Ȑ��l�͖{��̐ςɂ͖��Ӗ��ŁA
X�̉�2���͏��97�܂ł̌��ʂ������I�ɌJ��Ԃ��B�]���āA�{��̉��́A
�@�@3*7*13*17*23*�c*93*97
�̐ς̉�2���̐��������߂邱�ƂƓ����B
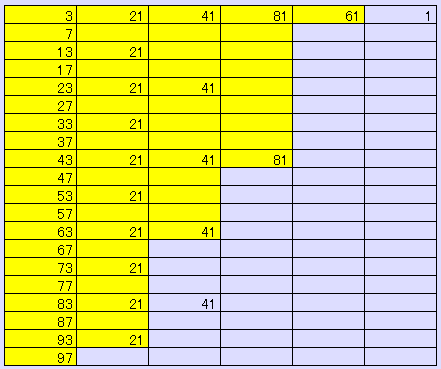
��̐}�ł͓s���̗ǂ����ƂɁA
�@�@3*7, 13*17, �c, 93*97
��2���̑g�ɂ����100�̏�]�͉���� 21 �ƂȂ�B
���l��2���g�ݍ��킹���ς̏�]���E�̗�ɋ��߂�� 61�B
�Ō�ɂ��� 61 �ƑɂȂ葹�˂� 41 �̐ς�100�̏�]�����߂�� 1�B
����ċ��߂���� 0 �ł���B
�E����4
�i�y���l�|���F�}�V���j
�y�z
3, 7, 13, 17, �c, 1993, 1997��1�̈ʂ�3�܂���7�̐����͓�������������B
���̃y�A(10a+3��10a+7�Ƃ���)���������
�@�@(10a+3)*(10a+7)=100a2+100a+21
�ƂȂ�̂�10�̈ʂ�21�݂̂Ɉˑ����邱�ƂȂ�
����Ė���21��200(a=0,1,�c,199)���10�̈ʂ����߂�������ƂɂȂ�B
21200=(20+1)200
=20200+(200C199)20199*11+�c+(200C1)201*1199+1200
�ƂȂ�̂�, 10�̈ʂ�0
�����@0
(�ʉ�)
21�̗ݏ��10�̈ʂ�1�̈ʂ��v�Z�����
21, 41, 61, 81, 01, 21�Əz����B�����200���10�̈ʂ́@0
�E����5
�i�y���l�|���F�X���[�N�}���j
3��7��10�̒��ɂP�g�����邩��...2000/10=200�g
3*7=21
21��212=41��213=61��214=81��215=01��216=21
25=01
200��5�̔{���Ȃ̂�...
2200=(25)40=140=1
10�̈ʂ�...�u0�v
�E����6
�i�y���l�|���F��ӂ����̂炢��������j
��̈ʂ�3��7�̐���2���y�A�ɂ��ĕ��ׂĂ݂܂��B
| No | �O | �� | �� |
|---|---|---|---|
| 1 | 3 | 7 | 21 |
| 2 | 13 | 17 | 221 |
| 3 | 23 | 27 | 621 |
| 4 | 33 | 37 | 1221 |
| ��� | ��� | ��� | ��� |
| 199 | 1983 | 1987 | 3940221 |
| 200 | 1993 | 1997 | 3980021 |
����2�̐ς͉��ꌅ��1�ɂȂ�܂��B
��̕\���݂�ƁA�e�s�̐ς̉���21�ɂȂ��Ă��܂��B����́A
�@�@(10k�{3)(10k�{7)��100k2�{(70�{30)k�{21��100(k2�{k)�{21
���A�[���ł��܂��B
�\�̈ʂ�������Ηǂ��̂ŁA21200 �̌v�Z���l����悢���ƂɂȂ�܂��B
�y�l���P�z
��̈ʂ��P�̂Q���̐��̏\�̈ʂ͏\�̈ʂ̐��̘a�ɂȂ�܂��B
�@�@(10m�{1)(10n�{1)��100mn�{(10m�{10n)�{1��100mn�{10(m�{n)�{1
�@211�̏\�̈ʂ�2
�@212�̏\�̈ʂ�4 (2�{2)�A
�@213�̏\�̈ʂ�6 (4�{2)�A
�@214�̏\�̈ʂ�8 (6�{2)�A
�@215�̏\�̈ʂ�0 (8�{2)
�ȍ~�́A�o2�A4�A6�A8�A0�p�̌J��Ԃ��ł��B
200��5�Ŋ�����̂ŁA�����́A0�ł��B
�y�l���Q�z
(20�{1)200 �̏\�̈ʂ̐���������悢�̂Ńp�X�J���̎O�p�`���l���܂��B
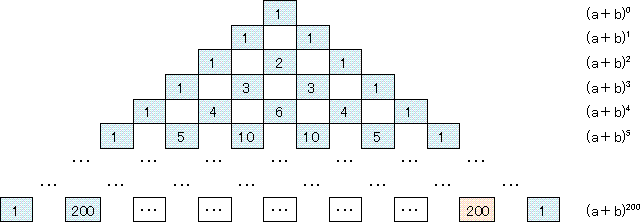
�W�J��201�1199�̍��̌W����200�Ȃ̂ŁA�\�̈ʂ�0�ł��B
�E����7
�i�y���l�|���F�G���h�X�j
�����͂O�ł��B10�̈ʂ������m�肽���̂ŁA�����邽�тɉ��ɂ���悤�ɂ��Čv�Z���܂����B
�P�O�iBASIC
CLEAR LET x=1 FOR i=1 TO 2001 IF MOD(i,10)=3 OR MOD(i,10)=7 THEN LET x=MOD(x*i,100) NEXT i PRINT x-MOD(x,10) END
�E����8
�i�y���l�|���F�l�c�@�����j
�Q�O�O�P�ȉ��̈�̈ʂ��R�̐��̐���
�@�@�R�C�P�R�C�Q�R�C�c�c�c�C�P�X�X�R
�ƁC�Q�O�O�P�ȉ��̈�̈ʂ��V�̐��̐���
�@�@�V�C�P�V�C�Q�V�C�c�c�c�C�P�X�X�V
�̂��ׂĂ̐ς��P�O�O�Ŋ������]����P�O�Ŋ������������ł���D
�@�ς��v�Z����Ƃ��ɂ́C���ꂼ��̂Ƃ��̂P�O�O�Ŋ������]������߂邾���ł悢�D
���̍l����p���ă}�N����������D
�@���͂O�ł���i�ς��P�O�O�Ŋ������]��͂P�ɂȂ�j�D
Option Explicit
Sub Macro1()
�@�@�@Sheets("Sheet1").Select
�@�@�@Dim X As Long
�@�@�@Dim n As Integer
�@�@�@Dim j As Integer
�@�@�@X = 1
�@�@�@For j = 3 To 7 Step 7 - 3
�@�@�@�@�@�@For n = j To 1990 + j Step 10
�@�@�@�@�@�@�@�@�@X = (X * n) Mod 100
�@�@�@�@�@�@Next n
�@�@�@Next j
�@�@�@Cells(1, 1).Value = X \ 10
�@�@�@Range("A1").Select
End Sub
�E����9
�i�y���l�|���F������͑����j
�ς̌��ʂ̏\�̈ʂ����߂�̂ŁA�S�̈ʈȏ�̕����͍l���Ȃ��Ă悢�B
�\�̈ʈȏオ�����ŁA��̈ʂ��R�ƂV�̐����̐ς́A
�@�@(M�~10+3)�~(M�~10+7)=M2�~100+M�~10�~(3+7)+21=(M2+M)�~100+21
�K���A���Q���́A21�ɂȂ�B���lX�́A�����������Q����21�̐����Q�O�O�̐ςł��邩��
���̉��Q���́A�@21200�ƈ�v����B�藝���g���ƁA
�@�@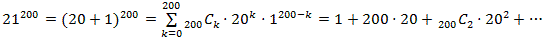
��Q���́@4000�@�@��3���ȍ~���@202�������ɂ��̂ŁA���Q���́A00
�]���āAX�̉�2���́A01�@�ɂȂ�B
�i�����j�@0
�E����10
 �i�y���l�|���F��̂�������j
�i�y���l�|���F��̂�������j
�����@�@�\�ʂ͂O�ł�
�Q�O�O�P�ȉ��̐����̒��ɂR�ƂV�͂Q�O�O����܂��B
�����̐ςw�͎��̒ʂ�ł�
�@�@�w���R�Q�O�O�~�V�Q�O�O���Q�P�Q�O�O
�w�̏\�ʂׂ܂��B
�@�@�Q�P�P���Q�P���Q
�@�@�Q�P�Q���S�S�P���S
�@�@�Q�P�R���X�Q�U�P���U
�@�@�Q�P�S���P�X�S�S�W�P���W
�@�@�Q�P�T���S�O�W�S�P�O�P���O
�@�@�Q�P�U���W�T�V�U�U�P�Q�P���Q
�@�@�Q�P�V���P�W�O�P�O�W�W�T�S�P���S
���̌��̌��ʂT�Ŋ�����Ώ\�ʂ͂O�ł���ƕ�����܂��B
�Q�O�O�͂T�Ŋ����܂��̂ŏ\�ʂ͂O�ƂȂ�܂��B
�E����11
�i�y���l�|���F�܂߁j
2011�N�������ōŌ�E�E�E������2011�ȉ��Ǝv������A2001�Ȃ�ł��ˁB
�ނ��A2001��2011�ł�1�Z�b�g�������Ȃ�����A
2011�Ȃ瓚���́u2�v�Ȃ�ł����A2001�̖��Ƃ��ĉ����܂��B
�o�W���u�Z���I�����s�b�N�v�Ȃ̂ŁA���w�����������̂Ƃ��āA
�܂��͏��w���ł������肻���ȉ������ŁB
��̈ʂ�3�܂���7�̐����������������珇�Ɏ��o���āA
2���ς����߂Ă݂�ƁA
�@ 3�~ 7�� 21
�@13�~17�� 221
�@23�~27�� 621
�@33�~37��1221
�@43�~47��2021
�@53�~57��3021
�@�E�E�E
�ƂȂ�A��2�����K��21�ł��邱�Ƃ�������B
�C���h���v�Z�@�̃A���ł��ˁB
���āA���ɂ����̐ς�����Ă����B
�������A�\�̈ʂ����߂�悢����A�v�Z���ʂ�100�ȏ�̕����͖������āA
�@21�~ 221��21�~21�� 441��41
�@41�~ 621��41�~21�� 861��61
�@61�~1221��61�~21��1281��81
�@81�~2021��81�~21��1701��01
�@01�~3021��01�~21��21
�Ȃ̂ŁA���ԂɊ|���Ă����Ə\�̈ʂ�2�A4�A6�A8�A0�Əz���邱�Ƃ�������B
2001�Ƃ������Ƃ́A���̌J��Ԃ������傤��40��Ȃ̂ŁA�����́u0�v�B
���Z�����炢�̐l�Ȃ玟�̂悤�ɉ����̂ł��傤���B
�܂��A���߂鐔�́A
�@��(10n�{3)(10n�{7)
�Ə�����B
�A���An��0�`199�ł���B
���̎���ό`���āA
�@��(10n�{3)(10n�{7)����{100n(n�{1)�{21}����(100an�{21)
�@��(100a0�{21)(100a1�{21)�E�E�E(100an�{21)�@���@A���Ƃ���
A����W�J���邱�Ƃ��l����ƁA21n+1�̍��ȊO�͑S��100�������Ɏ���
�܂�AA���ŏ\�̈ʂɊ֗^����̂�21n+1�̍��̂݁B
n�{1��m�Ƃ���2���藝��p����ƁA
�@21m��(20�{1)m
�@��mC0�E20m�{mC1�E20m-1�{
�E�E�E�{mCm-1�E201�{mCm�E200
�����ŁA202��4�E100�Ȃ̂ŁA202�ȏ�̍�����͂�S��100�������Ɏ��B
�����ŁAA����W�J�����ۂ�100�������ɂ��S�Ă̍�����A
���ʈ���100������o������������P�Ƃ���ƁAA����
�@��(10n�{3)(10n�{7)��100P�{20m�{1
�Ə����邱�ƂɂȂ�B
20m�̈�̈ʂ�0�ł��邩��A�J��オ����Ȃ��B
����āA�v�Z���ʂ̏\�̈ʂɊ֗^����̂�20m�̍��݂̂ł���B
�i�\�̈ʂ�����������蓾�Ȃ����Ƃ̏ؖ��ɂ��Ȃ��Ă���j
n��199���A20m��20(n�{1)��20�~200��4000�Ȃ̂ŁA�\�̈ʂ́u0�v
�l�@
����͈�̈ʂ�������10�ɂȂ邱�Ƃ��|�C���g�ɂȂ��Ă���悤�ł��̂ŁA
��̈ʂ�1��9�Ƃ��A2��8�Ƃ��ł��l���Ă݂܂����B
�E1��9�F��(10n�{1)(10n�{9)��100P�{9n
�@���̏ꍇ��9n���|�C���g�ƂȂ�B
�@���A9n�̏\�̈ʂȂ�Čv�Z������@�͂�����Ǝv�����Ȃ��B
�@���ۂɌv�Z����ƁA910�̏\�̈ʂ�0�ɂȂ�̂ŁA�����́u0�v�B
�@
�E2��8�F��(10n�{2)(10n�{8)��100P�{16n
�@����������ɂ͌v�Z�ł��Ȃ������ł��ˁB
�@�����A��������ۂɌv�Z���Ă݂�ƁA�\�̈ʂ�
�@1�A5�A9�A3�A7�̌J��Ԃ����ۂ�����A���̏ꍇ�̓����́u7�v�B
�@
�E4��6�F��(10n�{4)(10n�{6)��100P�{24n
�@����܂����ۂɌv�Z���Ă݂�ƁA�\�̈ʂ�2��7�̌J��Ԃ��ɂȂ��Ă���A
�@��͂蓚���́u7�v�B
�@
�E5�F��(10n�{5)
�@���ꂪ��ԓ�V�����B
�@����ς肱������یv�Z����ƁA�\�̈ʂ͍ŏ���0�̌�A
�@7�A7�A2�A2�̌J��Ԃ��Ȃ̂ŁA�ŏI�I�Ɂu2�v�ɍs�����܂��B
4��6�̏ꍇ�̏\�̈ʂ�2��7�̌J��Ԃ��Ȃ̂͂Ȃؖ��ł������ł��ˁB
�ɂȂƂ��ɂł��g���C���Ă݂�`���ƁB
�E����12
�i�y���l�|���FPart Marty�j
2001 �ȉ��̐��̐����̂����A��̈ʂ��R�܂��͂V�ł�����̂��ׂĂ̐ς��w�Ƃ���B
�w�̏\�̈ʂ����߂Ă��������B�܂��A�w�̏\�̈ʂ����߂�̂�����A100��]���Z��p���čl����B
���Q���������l����悭�A��̈ʂ��R�̏ꍇ�A03,13,23,33,43,53,63,73,83,93�̐ς�mod�����߂�B
�i3+0)*(3+10)*....*(3+80)*(3+90)=310+��n*10*39+......�Q�Ԗڂ܂ł̍����l����悢�B
mod(310,100)=mod(35,100)2=mod(43,100)2=49
mod(450*39,100)=mod(450,100)*mod(35,100)*mod(34,100)=mode(50*43*81,100)=50
�����mod(3+0)*(3+10)*....*(3+80)*(3+90),100)=49+50=99=-1�ł���
�e�v�f���Q�O������̂ŁA
��̈ʂ��R�̏ꍇ�́Amod((-1)20,100)=1�ƂȂ�B
��̈ʂ��V�̏ꍇ�A07,17,27,37,47,57,67,77,87,97�̐ς́A
-93-83,-73,-63,-53,-43,-33,-23,-13,-03�̐ςł���A
(40+50)*(-1)10=99=-1�ł���Amod((-1)20,100)=1�ƂȂ�B
��̈ʂ��R�ƈ�̈ʂ��V�̐ς͂P�ƂȂ�A�w�̏\�̈ʂ̐����́A�O�ƂȂ�B
���j��]���Z:mod(m, n)���� m �� n �Ŋ������Ƃ��A���̏�]�������B���L�̗l�ɁA���������̃\�t�gmaxima�Ŋm�F���܂����B
kill(all); nnn:1$for a:0 thru 2 do �@for b:0 thru 9 do �@�@for c:0 thru 9 do �@�@�@for d:0 thru 9 do �@�@�@�@if d=3 or d=7 then �@�@�@�@nnn:mod((a*1000+b*100+c*10+d)*nnn,100) $nnn;�@
�E����13
�i�y���l�|���F�]�ʔ����j
��̓I�Ɍv�Z�������������Ă݂�ƁA�ȉ��̒ʂ�B
�w=3�~7�~13�~17�~23�~27�~�c�~1993�~1997
�@=(3�~7)�~(10+3)�~(10+7)�~(20+3)�~(20+7)�~�c�~(1990+3)�~(1990+7)
�@=21�~(100+30+70+21)�~(400+60+140+21)�~�c�~(3960100+5970+13930+21)
�@=21�~(200+21)�~(600+21)�~�c�~(3980000+21)
���āA���̌v�Z���ɂ����āA�w�̏\�ʂɉe������̂�21������S�Ċ|�����킹�����̂ł���B
21�͑S����200����̂ŁA21200�@�������̑ΏۂƂȂ�B
��̓I�ɏ��������Ă݂�ƁA�ȉ��̒ʂ�B
�@211=21
�@212=21�~21=441
�@213=441�~21=9261
�����ŁA�\�ʂɉe������͉̂��̐����Ȃ̂ŁA441�~21�ɂ��ẮA41�~21���l����Ηǂ��B
�@213 �F 41�~21=861
�@214 �F 61�~21=1281
�@215 �F 81�~21=1701
�@216 �F 1�~21=21
�@217 �F 21�~21=441
�@218 �F 41�~21=861
�@�@�E�E�E
�ȏ���A21n�ɂ��āAn=1,2,3,4,5,6,7,8�E�E�E�ɑ��āA�\�ʂ̐����́A
2,4,6,8,0,2,4,6�E�E�E�Əz����B
���@n=200�̏ꍇ�A�\�ʂ̐�����0�ł���B
���@�w�̏\�̈ʂ̐�����0�ł���B
�E����14
�i�y���l�|���F�I���W�j
���߂�X�̂P�O�̈ʂ̐��́A�ς����ƂP�O�O�ȏ�̐��́A�P�O�O�����̐��ɂ͉e�����Ȃ��̂�
�F�@mod100�@�ōl����Ώ\���ł���B������
�@�@�R�~�P�R�~�Q�R�~�R�R�~�S�R�~�T�R�~�U�R�~�V�R�~�W�R�~�X�R�߂X�X�߁|�P�@mod100�@�E�E(1)
���l��
�@�@�X�V�~�W�V�~�V�V�~�U�V�~�T�V�~�S�V�~�R�V�~�Q�V�~�P�V�~�V
�@�߁i�|�R�j�~�i�|�P�R�j�~�i�|�Q�R�j�~�i�|�R�R�j�~�i�|�S�R�j�~�i�|�T�R�j�~�i�|�U�R�j�~�i�|�V�R�j�~�i�|�W�R�j�~�i�|�X�R�j
�@�߂R�~�P�R�~�Q�R�~�R�R�~�S�R�~�T�R�~�U�R�~�V�R�~�W�R�~�X�R�߂X�X�߁|�P�@mod100�@�E�E(2)
�]����
�P�`�P�O�O���̂P�̈ʂ��R�܂��͂V�ł�����̂̐ςłP�O�ȉ��̐��́A(1)�@(2)���
�@�@�R�~�P�R�~�Q�R�~�E�E�E�~�X�R�~�V�~�P�V�~�Q�V�~�E�E�E�~�X�V�߁@�P�@mod100�@�E�E�i�T�j
����� �P�`�Q�O�O�P�ȉ��̂P�̈ʂ��R�܂��͂V�ł�����̂̐ςłP�O�ȉ��̐��́A
�i�T�j�̂Q�O��@�]����
�@�@�R�~�V�~�P�R�~�E�E�E�~�P�X�X�R�~�P�X�X�V�߁@�P�Q�O�@�߁@�P�@mod100
�@���@X�̏\�̈ʂ̐����O
�E����15
�i�y���l�|���F�\�t�B�A�A�N�g�D�[�_�j
X��3�~7�~13�~17�~23�~27�~�E�E�E�~1993�~1997
�@��(3�~7)�~{(10+3)�~(10+7)}�~{(20+3)�~(20+7)}�~�c�~{(1990+3)�~(1990+7)}
�@��21�~(102 + 10�~10 + 21) �~(202 + 20�~10 + 21) �~�E�E�E�~(19902 + 1990�~10 + 21)
�����W�J����ƁA
X��100N�{21200�@�iN�͐����j�ƂȂ�B
����M�̉�2����F(M)�ŕ\���ƁA
�@F(211) = 21
�@F(212) = 41
�@F(213) = 61
�@F(214) = 81
�@F(215) = 01
�@F(216) = 21
�@�c
�ƂȂ�̂ŁCF(21200)��01
���������āCX�̏\�̈ʂ�0�D
�E����16
�i�y���l�|���F���߂��[�j
�S�̈ʈȏ�̐����ɂǂ�Ȑ����������Ă��\�̈ʂɉe�����Ȃ��̂�mod100�ōl����悢�B
�@�@�w��3�~7�~�c�~93�~97�~103�~107�~�c�~1993�~1997
�@�@�@��(3�~7�~�c�~93�~97)�~(3�~7�~�c�~93�~97)�~�c�~(3�~7�~�c�~93�~97)�@���J�b�R20��
�J�b�R���ɂ��āAa��0�܂��͈ꌅ�̎��R���Ƃ����
�@�@(10a�{3) (10a�{7)��100 (a2�{a)�{21��21
���
�@�@(3�~7)�~�c�~(93�~97)��2110��((21�~21)�~(21�~21�~21))2��(41�~61)2��12��1
�����
�@�@�w��120��1
���߂鐔�͏\�̈ʂȂ̂łO
�E����17
�i�y���l�|���FRyu1128�j
2001�ȉ��̐��̐����̓��A1�̈ʂ�3��7�̐�����ׂ��
�@�@3,7,13,17,23,27,�E�E�E�E1993,1997
�ł��B1����10�܂ł̊Ԃ�1�̈ʂ�1�Â�3��7���܂܂��̂�
�e�X2001�܂ł�200�Âo�Ă��܂��E�E�E�E�E(1)
���̐���̐ς�����������2�����܂Ƃ߂܂�
�@�@�w=(3�~7)�E(13�~17)�E(23�~27)�E(33�~37)�E�E�E�E�E�E(1993�~1997)
�i�j�����ƍl���A���Ԗڂ̐ςɒ��ڂ��܂��B
���Ԗڂ̐ς�
�@((��-1�j�~10+3) �~((��-1�j�~10+7)
=((��-1�j�~10)2�@+�@(3+7) �~((��-1�j�~10)�@+�@3�~7
=100 �~�i (��-1�j2�@+ (��-1�j)�@+�@21
�ƂȂ�A10�̈ʂ͏��2�A1�̈ʂ͏��1�ƂȂ�܂�100�̈ʈȏ�̕�����
�w��10�̈ʂɉe�����܂���A�w��10�̈ʂ����߂�ɂ͌���
�@�@21200�E�E�E�E�E(2)
��10�̈ʂ����߂�悢���Ƃ�����܂��B
������(2)�����̂悤�ɕό`��2���W�J���l���Č��܂��B
�@�@(2)=(20+1)200
����2���W�J��20�ׂ̂��悪10�̈ʂɂƂǂ܂�̂�1��0�����ł��̎���2���W����200��1�ł��B
�܂�200�~201�~1199�@+�@1�~200�~120�E�E�E(3)
�ׂ�悢�킯�ł����4001�ƂȂ�10�̈ʂ�0�ƂȂ�܂��B�E�E�E�E����
�E����18
�i�y���l�|���F�܂��j
����: 0�ł��B
�v�Z�@���g���ĉ����܂����B
(define (seq start end)
; start -- inclusive end -- exclusive (if (>= start end)
'()
(cons start (seq (+ start 1) end))))
(define (remove test l) (apply append (map (lambda (e) (if (test e) '() (list e))) l)))
(define (tens_digit n) (modulo (quotient n 10) 10))
(define (main args) (display (tens_digit (apply *
(remove (lambda (n)
(let ((r (modulo n 10)))
(not (or (= r 3) (= r 7)))))
(seq 1 2002))))) (newline))
scheme�Ńv���O����
#includeintmain(){ int i, x; for (i = x = 1; i <= 2001; i++) { if (i % 10 == 3 || i % 10 == 7) { x = x * i % 100; } } printf("%d\n", x / 10); return 0;}
C����Ńv���O����
�ǂ���̃v���O�������A��蕶��f���Ɏ��s���Ă��邾���ł��B�������A�����ɈႢ������܂��B
scheme�Ńv���O�����́A�ŏ���1�`2001�̃��X�g�����A���̃��X�g�����̈ʂ�3�܂���7�̂��̂�����
�I��(�ʂ�)���X�g�����A���̗v�f�̂��ׂĂ̐ς�(1147���̐��ł�)���߁A���̏\�̈ʂ������o���Ă��܂��B
����AC����Ńv���O�����́A�ŏ��ɁAx��1�ɂ��Ă����Ai��1����2001�܂�1�Â��₵�Ȃ���A�����A
i�̈�̈ʂ�3�܂���7��������ux * i % 100�v���v�Z�����̒l��x�̐V�����l�Ƃ��čĐݒ�A
�Ō�ɁA���̎��_��x�̏\�̈ʂ������o�Ă��܂��B
�v���O���������݂��C����Ńv���O�����̕����V���v���ɂ݂��܂����A����Ƃ͗����ɁA
�u�v�Z�̎菇�v�����ƍׂ����w������Ă����肷�邤���A�Ō�̎��_�ŁAx�̒l��X�̉��ɂȂ��Ă���
�Ƃ����̂��A���܂莩���ł͂���܂���B
�E����19
�i�y���l�|���F���q�̗Y�L�j
2001 �ȉ��̐��̐����̂����A��̈ʂ��R�܂��͂V�ł�����̂̏W����
A�oa1,a2,a3 , ....�p�Ƃ����A�W��A�Ɋ܂܂�鐮�����ׂĂ̐ς��w�Ƃ���B
�W��A�Ɋ܂܂�鐮���́Aw,x,y,z�����ꂼ��0����9�܂ł̐����Ƃ���
�@�@1000�~ w �{ 100�~ x �{10�~y �{ 3
�܂���
�@�@1000�~ w �{ 100�~ x �{10�~y �{ 7
�Ƃ���킹��B
�w�̏\�̈ʂ����߂�ɂ́AX mod 100 ���v�Z����Ώ\���Ȃ̂ŁA�ςƏ�]�̐���
��A�v�Z�r����100�ȏ�̈ʂ͖������Ă��܂�Ȃ��B
��̈ʂ��R�ł��鐮���ƈ�̈ʂ��V�ł��鐮���͓������������݂���̂ŁA�܂�
213,217�̂悤�ɏ\�ȏ�̈ʂ������������m�̐ς��v�Z���Ă݂�B
�@�@�i1000�~ w �{ 100�~ x �{10�~y �{ 3�j�~�i1000�~ w �{ 100�~ x �{10�~y �{ 7�j�@mod100
�@�@���i10�~y �{ 3�j�~�i10�~y �{ 7�j�@mod100
�@�@���i100�~y�~y�{70�~y �{ 30�~y �{ 21�j�@mod100
�@�@���i100�~y�~y�{100�~y �{ 21�j�@mod100
�@�@���i21�j�@mod100
�����X�̏\�̈ʂ�21�����悩�����l�̏\�̈ʂł���B���āA1����100�̊Ԃɂ�
��̈ʂ��R�܂��͂V�ł��鐮�������ꂼ��10���݂���̂ŁAX�̏\�̈ʂ͂�21
��10������悩�����l�A�܂�21��5���2������悩�����l�̏\�̈ʂƓ����ł���B
21��5���4084101�ł���̂ŁAX�̏\�̈ʂ�1�����悩�����l�̏\�̈ʂƓ����ł�
��B1�����悵�悤���l��1�̂܂܂Ȃ̂ŁAX�̏\�̈ʂ�0�B
�E����20
�i�y���l�|���F-hiryu�j
��̈ʂ��R�ł��鐔���ƂV�ł��鐔���́A
���ꂼ��P�`�P�O�̒��ɂP���A�P�P�`�Q�O�̒��ɂP���A�c�A�P�X�X�O����Q�O�O�O�̒��ɂЂƂ�����B
�i�P�O���{�P�j�`�i�P�O���{�P�O�j�i�������A�O�������P�X�X�j�̒��ŁA
��̈ʂ��R�ł��鐔���͂P�O���{�R�A��̈ʂ��V�ł��鐔���͂P�O���{�V�Ƃ���킳���B
������������ƁA
�@�@�@�i�P�O���{�R�j�i�P�O���{�V�j
�@�@���P�O�O��2�{�i�R�{�V�j�P�O���{�Q�P
�@�@���P�O�O�i��2�{�P�j�{�Q�P
�ƂȂ�B
����āA�ǂ̂悤�Ȃ����Ƃ��Ă��A�i�P�O���{�P�j�`�i�P�O���{�P�O�j�i�������A�O�������P�X�X�j�̒��ł�
��̈ʂ��R�ł��鐔���ƂV�ł��鐔���������������̉��͂Q�P�ɂȂ�B
�O�������P�X�X�ł���A�w�͂Q�O�O�P�ȉ��̐��̐����̂����A��̈ʂ��R�܂��͂V�ł�����̂��ׂĂ̐ςł��邩��A
���̏\�̈ʂ͂Q�P�̂Q�O�O��Ɠ����ɂȂ�B
�܂��A
�@�@�@�Q�P1���Q�P
�@�@�@�Q�P2���S�S�P
�@�@�@�Q�P3���S�S�P�~�Q�P���X�Q�U�P
�@�@�@�Q�P4���X�Q�U�P�~�Q�P���P�X�S�S�W�P
�@�@�@�Q�P5���P�X�S�S�W�P�~�Q�P���S�O�W�S�P�O�P
�@�@�@�Q�P26���S�O�W�S�P�O�P�~�Q�P���W�T�V�U�U�P�Q�P
�����ŁA�����Q�P�ɂȂ����̂ŁA�\�̈ʂɒ��ڂ���ƁA
�@�@�@�Q�@���@�S�@���@�U�@���@�W�@���@�O�@���@�Q�@���@���
�ƂȂ�A�@�u�Q���S���U���W���O�v�@���J��Ԃ��Ă���B
�����ŁAX�̉��͂Q�P200�Ɠ����ł������B
�Q�O�O���S�O�~�T�ƕ\�����Ƃ��ł���̂ŁAX�̏\�̈ʂ͂O�ł���B
�E����21
�i�y���l�|���F�O�p��K�j
1�̈ʂ�3�܂���7�ł���A������2����10k�{3�C10k�{7�ik��0�C1�C2�C�c�j�Ə�����B
�����́C�����������珇��2n�{2�̐ς�an�Ə�����
�@�@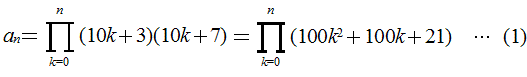
an�̉�2����an��100�Ŋ������]��ł���C(1)���
�@�@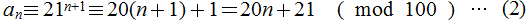
(2)���Can��10�̈ʂ́Cn��0�C1�C�c �̂Ƃ��C2�C4�C6�C8�C0�C2�C�c �Ǝ���5�ŕω�����B
���߂���̂�a1999��2�̈ʂŁCn��0��2���琔����2000��5�~400�Ԗڂł��邩��C����́@0 �c[��]
�R�����g
��̈ʂ��R�̐����V�̐����y�A�ɂ��Đς��l����ƁA
�K�����Q�����u�Q�P�v�ƂȂ��Ă��܂��B
�@�@(10k�{3)(10k�{7)��100k2�{(70�{30)k�{21��100(k2�{k)�{21
�u�R�{�V���P�O�v���|�C���g�ł��ˁB����ɂ��ẮA�܂߂������l�@���Ă��������܂����B
���̖��́A�\�̈ʂ����߂����킯�ł�����A���Q�������ɒ��ڂ���悢�킯�ł��B
�Ƃ��낪�Q�P�̐ς��v�Z���Ă݂�ƁA���Q���͎����I�ɕω������邩��A��͂Q�P��������悢���Ƃ������Ƃ�
�A�������킯�ł��ˁB
���݂ɁA���w�I�����s�b�N�\�I���̃I���W�i���́A�u�Q�O�P�P�ȉ��́v�ƂȂ��Ă��܂��ˁB ���������āA�́u�Q�v�ł��B���炵�܂����B
 top
top