問題187　正十二角形の秘密

辺の長さが１の正十二角形の面積は、辺の長さが１の正三角形ｘ個と辺の長さが１の正方形ｙ個の面積を加えたものとなる。ｘと y を求めてください。

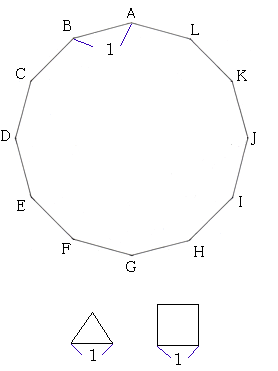
問題の出典

キュートな数学名作問題集
小島寛之著

解答

～到着順にご紹介します～

解答・その1

（ペンネ－ム：浦岡）

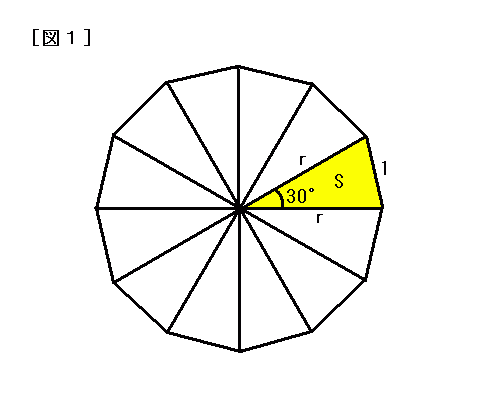
【解答１】
正三角形の面積=√3/4、正方形の面積=1より、正十二角形の面積=(√3/4)x+y ･･･☆とおける。
ここで、図１のように、黄色の三角形の面積をSとすると、S=(1/2)*r²*sin30° ･･･[1]
また、余弦定理より、1=r+r-2*r*cos30° ∴r=2+√3 ･･･[2]
[1][2]より、S=(2+√3)/4
したがって、正十二角形の面積=12S=6+3√3 ･･･★
☆★より、x=12、y=6

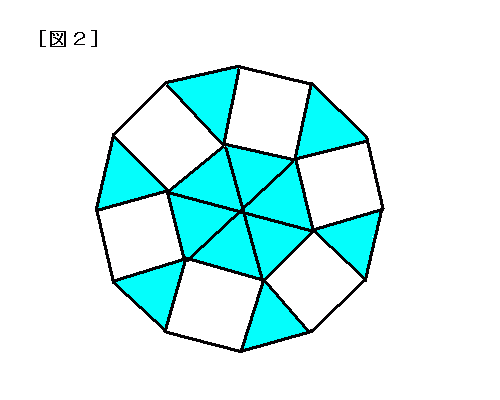
【解答２】
正三角形の内角=60°、正方形の内角=90°、正十二角形の内角={180°(12-2)}/12=150°であり、
60°+90°=150°と、それぞれの辺の長さに着目すると、
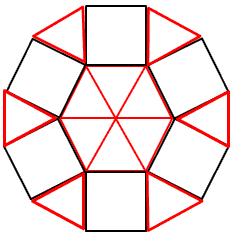
図２のように、正三角形と正方形を正十二角形の内部に隙間なく敷き詰めることができる。
よって、正三角形の個数=x=12、正方形の個数=y=6

（補足）
解答１は三角関数を利用した自然な解法で、図形的考察もほとんど必要なく平易。
解答２は直感によるもので視覚的に明快ではあるが、いつでも上手くいくとはかぎらない。
ただし、問題のタイトルに『正十二角形の秘密』とあるので、
興味深い性質を発見することが今回の趣旨であり、解答２の方を期待された問題といえる。

解答・その2

（ペンネ－ム：スモークマン）

正十二角形が内接する円の半径を x とすると...
面積=x²*sin(π/6)*6=3*x²
１辺が1なので...
1²=2x²-2x²*cos(π/6)=x²*(2-√3)
x²=2+√3

正三角形の面積=√3/4
正方形の面積=1
正十二角形の面積=3*(2+√3)=6+3√3

から...△の数：x=12, □の数：y=6 個
見事な分解図を期待してます ^^v

解答・その3

（ペンネ－ム：転位反応）

角度に着目して考察する。
正十二角形の内角は１５０°である。150＝９０＋60より、下図の通り、
正方形と正三角形の組み合わせでその角を作ることができる。
さらに、新たに生じた内側の角１２０°は、二つの正三角形で作ることができる。

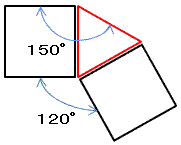
以上の考察から、正十二角形の構造は、
正六角形の各辺に正方形が接し、その正方形の間を正三角形がうめる構造をしている。
∴正三角形x＝１２個、正方形y＝６個である。

解答・その4

（ペンネ－ム：浜田　明巳）

　１辺の長さが１の正三角形と正方形の面積はそれぞれ，
　　√３／４，１
　この正十二角形の外接円の中心をＯとし，ＯＡ＝ｒとする．
　△ＯＡＢにおいて，余弦定理から，
　　ＡＢ^２＝ＯＡ^２＋ＯＢ^２－２・ＯＡ・ＯＢ・cos∠ＡＯＢ
　　∴１^２＝ｒ^２＋ｒ^２－２ｒ^２・cos(２π／１２)
　　∴１＝ｒ^２(２－√３)
　　∴ｒ^２＝１／(２－√３)＝２＋√３
　　∴△ＯＡＢ＝１／２・ＯＡ・ＯＢ・sin∠ＡＯＢ＝１／２・ｒ^２・sin(２π／１２)＝１／２・(２＋√３)・１／２＝(２＋√３)／４
　故に正十二角形の面積Ｓは，
　　Ｓ＝１２△ＯＡＢ＝１２・(２＋√３)／４＝６＋１２・√３／４
　また，
　　Ｓ＝√３／４・ｘ＋ｙ
　ｘ，ｙは非負整数，√３／４は無理数なので，
　　ｘ＝１２，ｙ＝６

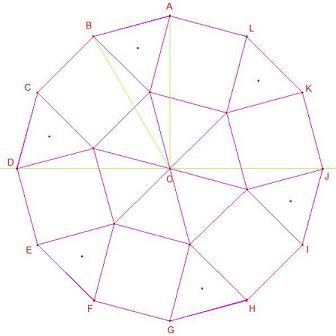
　ＣＡＢＲＩを使って，正十二角形を実際に作図すると，確かに正三角形が１２個，正方形が６個あることが分かる．

解答・その5

（ペンネ－ム：のっこん）

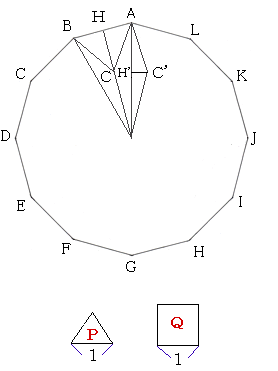
正十二角形の１つの頂点をA、その隣りの頂点をBとする
この正十二角形に外接する円の中心をOとする
辺の長さが1の正三角形の面積をP、辺の長さが1の正方形の面積をQとする

△OABは頂角30°の二等辺三角形である
OからABに垂線を下し、その足をHとする
OH上に点CをAC=ABとなるようにとると
△CABは辺の長さが1の正三角形となる・・・・・・・[1]

∠OAC=15°∠ACO=150°だから∠COA=15°
よって△COAはAC=CO=1の二等辺三角形になる
また△CBO≡△COAである

△CBOをOを中心に30°回転しOBをOAに重ねると
辺の長さが1のひし形ができる
このひし形をC´ACOとすると
∠C´AC=30°だから
C´からACに垂線を下し、その足をH´とした時
C´H´=1/2となる
よってひし形C´ACOの面積=1/2・・・・・・[2]

[1]、[2]より
△OABの面積=P+（Q/2)・・・・・・・[3]

[3]の右辺を12倍すると12P+6Q
従って　x=12 y=6

解答・その6

（ペンネ－ム：次郎長）

正十二角形の中心をＯとして、ＯＡ、ＯＢを結ぶと、三角形ＯＡＢは30・75・75度の二等辺三角形
ＡＢ（一辺１）のＯ側にＰＡ＝ＰＢ＝１となるように点Ｐを取ります。
同様にＣＤの内側にＱを取ります。
すると、三角形ＯＰＱも一辺１の正三角形となり、なんと、四角形ＢＣＱＰは一辺１の正方形となります。
これは、角度から証明できます。
各辺に対して同様の作業？をすると、
点Ｏの周りに正三角形が６個、その周りに正三角形が６個＋正方形６個ができます。
「正十二角形の秘密」って何だろうって考えていたのですが、内側の正三角形の頂点が正十二角形の頂点と１５度傾いているところなんでしょうね。

解答・その7

（ペンネ－ム：夜ふかしのつらいおじさん）

図のように正十二角形の辺のところに、正三角形をつくります。（黄色の正三角形１２個）
次に隣り合う正三角形の頂点を結びます。（空色の二等辺三角形１２個）
次に正三角形の頂点と正１２角形の中心とを結びます。（白色の二等辺三角形１２個）

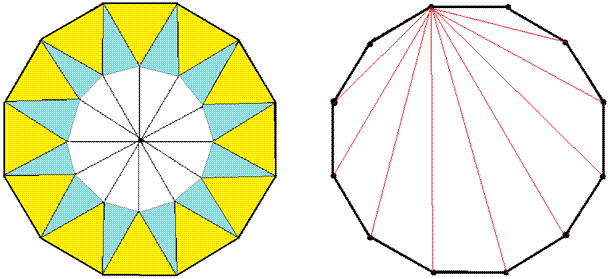
正十二角形に図のように対角線を引くと、１２－２＝１０個の三角形に分かれます。
だから、正１２角形の一つの内角は、１８０°×１０÷１２＝１５０°です。
空色二等辺三角形のとんがった方の角の大きさは、１５０°－２×６０°＝３０°です。（底角は７５°）
白色の二等辺三角形のとんがった方の角の大きさは、３６０°÷１２＝３０°です。（底角は７５°）
空色と白色の二等辺三角形は、底辺を共有しています。（１辺とその両端の角）
だから、この二つの二等辺三角形は合同になります。
この２つの二等辺三角形を図のように置き、等積変形をします。
すると、白の部分は、高さが1／２になります。
つまり、２等辺三角形４個で、１辺の長さが１の正方形になります。

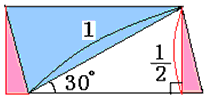
以上から、１辺１の正三角形を１２個、１辺１の正方形を６個合わせたものが、１辺１の正十二角形と同じ面積になります。

解答・その8

（ペンネ－ム：Ｒｙｕ1128）

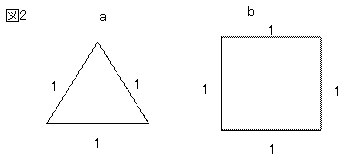
１辺１の正三角形と正方形を図２のように各々ａ、ｂとします。
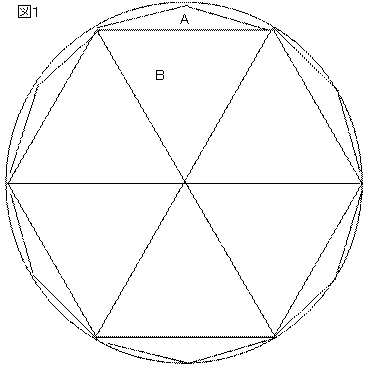
正１２角形を図１のように分割します
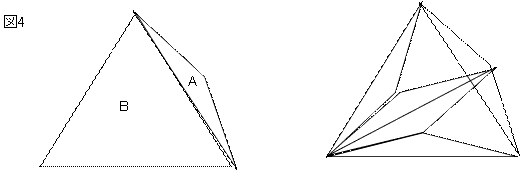
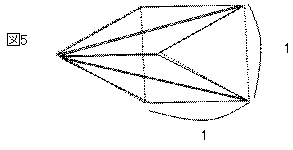
ＡＢに注目し図４のように組みなおすと
ＡＢはＡ×4+ａ×2であることが解ります
また、図５で示すとおりＡ×4＝ｂであることが解ります
従って、Ａ+Ｂ＝ｂ＋２ａとなります。
正１２角形は６×（Ａ+Ｂ）なので
6ｂ+12ａに等しくなります
よってｘ＝12、ｙ＝6　　・・・・回答

別解１
ａの面積は√3/4、ｂの面積は1
正１２角形の面積Ｍは外接円の半径をｒとすると
　　ｒ×ｒ×sin30度×1/2×12＝3ｒ²
1×sin75度＝ｒ/2から
　　ｒ＝（1+√3）×√2×1/2
なので
　　Ｍ＝3√3+6＝12×（√3/4）+6
よってｘ＝12、ｙ＝6

別解２

解答・その9

（ペンネ－ム：オヤジ）

正１２角形の半径 r をとすると、頂点を１個づつ飛ばした正６角形の一辺も r より、
第２余弦定理から、

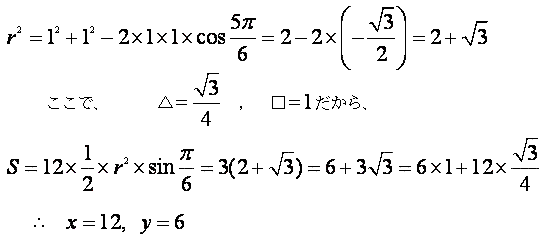
解答・その10

（ペンネ－ム：杖のおじさん）

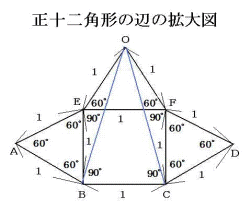
正十二角形の中心Ｏから辺Ｂ点。Ｃ点を結ぶ△は二等辺三角形になります。
∠ＢＯＣ＝３６０°÷１２＝３０°
∠ＯＢＣ＝（１８０°－３０°）÷２＝７６°
∠ＡＢＣ＝７５°×２＝１５０°
１５０°＝９０°＋６０°になります。
一辺１とする正方形の隣には一辺１とする正三角形が並べられる事が分かります。
従って、周囲には□が６個、△が６個出来ます。
中心には一辺１とする正三角形６個による正六角形が出来ます。
∠ＥＯＦ＝３６０°÷６＝６０°
答えは
x△＝６個＋６個＝１２個です。
y□＝６個です。

解答・その11

（ペンネ－ム：まーりんａｎｄさとりん）

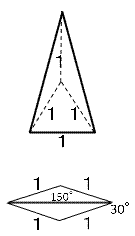求める正12角形の面積をＸとし、左の三角形の面積をＹとすると
　Ｘ＝１２Ｙ
Ｙは「１辺の長さ１の正三角形１つ」と
「頂角１５０°等辺の長さ１の二等辺三角形２つ」の和である。
「１辺の長さ１の正三角形１つ」の面積はｘ
「頂角１５０°等辺の長さ１の二等辺三角形２つ」の面積は、
左の図から内角が１５０°と３０°のひし形の面積と等しく、
これは辺の長さ１と1/2の長方形の面積と等しい。
よって、面積は0.5ｙとなる。
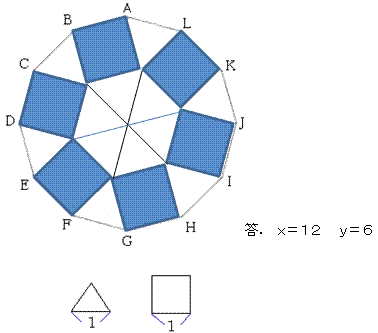
　　Ｘ＝１２（ｘ＋0.5ｙ）＝１２ｘ＋６ｙ
答．　ｘ＝１２　　ｙ＝６

別解

解答・その12

（ペンネ－ム：haya）

答： x=12, y=6
【解き方】

解答・その13

（ペンネ－ム：SOU）

正三角形,正方形,正十二角形の面積は各々
　　　√3/4 , 6 + 3√3 , 1
で与えられる。従って、正方形の個数をA、三角形の個数をBとして
　　　1xA + √3/4xB = 6 + 3√3
を解くことになるが、A,B は自然数なので、
　　　(4A-24) + (B-12)√3 = 0
とした時、A = 6,B = 12 が必要。
以上から正方形が6個、正三角形が12個という組合せが答えで、
また、これ以外の組合せは存在しない。

解答・その14

（ペンネ－ム：三角定規）

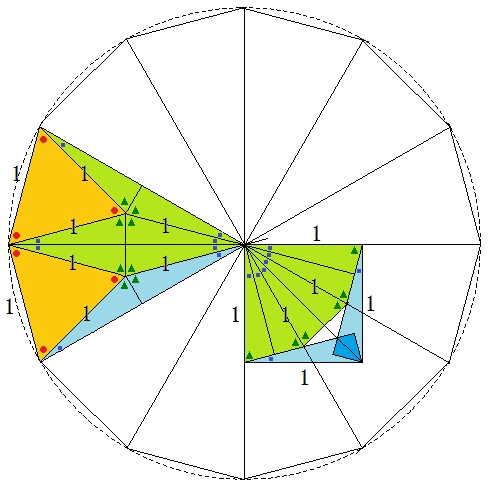
1辺が1の正十二角形は，12個の二等辺三角形（底辺1，頂角30°，底角75°）からなるが，それらのうちの2個は図に着色したように，1辺が1の正三角形2個（●は60°）と， 8個の直角三角形（内角が15°（■），75°（▲））に分割できる。
8個の直角三角形は，並べ替えれば右側のような1辺が1の正方形を作るが，青く重なっている部分は白色の部分と合同だから面積が等しい。
よって，
　2個の二等辺三角形＝2・△＋1・□
　∴ 正十二角形＝12・△＋6・□　［答］

解答・その15

（ペンネ－ム：やなせ）

１辺１ｃｍの正１２角形の面積と正三角形の面積はここで調べました。
数学公式集これによると正１２角形の面積は１１．１９６cm²
正三角形は０．４３３cm²　（数をｙとして）
正方形は当然１cm²　　　（数をｘとして）
ｘ＋０．４３３ｙ＝１１．１９６　といった式が成り立ちます。
連立方程式ではないから、ここからは全く数学的では無いけれど
正方形の数は偶数と思われるので
１１．１９６から
－２、－４､－６と引いた数の中でぴったし０．４３３で割り切れるのを探しました。
正方形が２個の場合　　９．１９６÷０．４３３＝２１．２３７８・・・・
　　　　　　４個の場合　　７．１９６÷０．４３３＝１６．６１８９・・・・
　　　　　　６個の場合　　５．１９６÷０．４３３＝１２（ぴったりです。）
よって
正三角形の数ｘは１２個
正方形の数ｙは６個

解答・その16

（ペンネ－ム：ちょろんは太太）

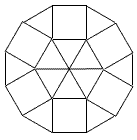
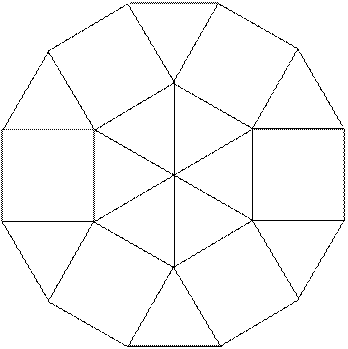
正十二角形を上記のように分割すれば、6個の正方形と12個の正三角形から成ることがわかる。
答　x=12, y=6

解答・その17

（ペンネ－ム：T_Tatekawa）

tan [pi/12] を求める．三角関数の倍角の公式から，
　　2 * tan[pi/12] / (1- tan[pi/12]² ) = tan[pi/6]
よって
　　tan[pi/12]² /sqrt[3] + 2 * tan[pi/12] - 1 /sqrt[3] =0
tan[pi/12] ＞ 0 より
　　tan[pi/12] = 2-sqrt[3]
辺の長さが1の正十二角形の面積は，底辺の長さを1，頂角の大きさを
[pi/6] とする二等辺三角形12個分．二等辺三角形1つの面積は，
　　2 * (1/2) * (1/2)/tan[pi/12] / 2 = (2+sqrt[3])/4
なので，辺の長さが1の正十二角形の面積は
　　12 * (2+sqrt[3])/4 = 3 * (2+sqrt[3])
一方で，辺の長さが1の正三角形の面積は
　　1 * (1*sin[pi/3])/2 = sqrt[3]/4
なので，辺の長さが1の正十二角形の面積は
辺の長さが１の正三角形 12 個と辺の長さが１の正方形 6 個の面積を加えたものとなる．

正方形の面積＝１で有理数、正三角形の面積＝√３/４で無理数です。正十二角形の面積をこの２者の和とするところから、アプローチするやり方と、正方形と正三角形で正十二角形を埋め込むという幾何学的なやり方に大別されましたね。

Challenge!