Weekend Mathematics乛栤戣乛栤戣31
俁侾丏慺悢偺栤戣
擸傔両僷僗儔亅(挧愴偦偺侾)
傾儞僕僃儔丒僼僅僢僋僗丒僟儞曇
孾妛弌斉
乮儁儞僱亅儉丗偝偩傗傫乯
堦偺埵偑嬼悢偺傕偺偼2偺攞悢偱偡偐傜慺悢偱偼偁傝傑偣傫丅
巆傝偺偆偪丆堦偺埵偑5偺傕偺偼5偺攞悢偱偡偐傜慺悢偱偼偁傝傑偣傫丅
偦偺巆傝偺壓偺埵偼
9丆987丆9876543丆987654321丆乧乧
偺孞傝曉偟偱偡偑丆偄偢傟傕丆3偺攞悢偱丆忋偺埵丂987654321亊乮10偺椵忔乯傕傑偨
3偺攞悢偱偡丅
埲忋偵傛傝丆
偁傞傕偺偼丆2傗5偺丆懠偺傕偺偼3偺攞悢偵側傝丆慺悢偼側偟丅丂
丂丂丂丂丂丂丂丂
丂丂摎偊丂夝側偟
姶憐
傁偭偲尒偰丆乽偙傟偼巹偵偼柍棟乿偲巚偄傑偟偨丅
柍尷偵懕偔偲側傞偲堦斒夝偵側傝偦偆偱巹偺擻椡傪挻偊傞偲巚偭偨偺偱偡丅
偦傟偱,堦斣彫偝偄慺悢傪尒偮偗偰,乽搘椡徿乿傪偹傜偆偲偄偆偐惤堄傪尒偣傛偆丠偲
巚偄傑偟偨丅
偲偙傠偑丆孞傝懼偊偟晹暘偼3偺攞悢偵側傞偙偲丆壓偺埵偼2偐3偐5偺攞悢偵側傝0屄
偲傢偐傝傑偟偨丅
乽庢傝偁偊偢丆傗傠偆偲偟偰傒傞乿偺偑傛偐偭偨偲巚偄傑偡丅
幚嵺丆偙傟偱丆傕偟丆
堦斣彫偝偄慺悢偑尒偮偐偭偨偲偟偨傜丆巹偵偼庤偵晧偊側偐偭偨偱偟傚偆丅

乮儁儞僱亅儉丗Chee乯
[夝摎]
傑偢偼丄俀偮偽偐傝曗戣傪
乮摉偨傝慜偱(丠)曗戣偲偄偆偺傕偍偙偑傑偟偄偺偱丄徹柧偼屻偱乯丅
曗戣侾乯
俁偮偺楢懕偡傞悢乮偲傝偁偊偢侾乣俋偵尷掕乯偐傜嶌傜傟傞悢偼俁偱妱傝愗傟傞丅
偨偲偊偽丄俋俉俈傗俇俆係側偳丅
曗戣俀乯
俁偱妱傝愗傟傞悢偺屻傠偵丄俁偱妱傝愗傟傞悢傪懕偗偰嶌偭偨悢偼丄
俁偱妱傝愗傟傞丅
偨偲偊偽丄俁偺屻傠偵俋傪懕偗偰偮偔偭偨俁俋側偳丅
傑偢丄俋乮俁偱妱傟傞乯傕俋俉乮俀偱妱傟傞乯傕慺悢偱側偄偺偱丄
俋俉俈埲崀偺悢楍偵偮偄偰峫偊傑偡丅
偮傑傝丄俁寘埲忋傪憐掕偟傑偡丅
偙偙偱丄梌偊傜傟偨悢楍偺偦傟偧傟偺悢傪丄
乽忋偺寘偐傜俁寘偢偮嬫愗傝丄偁傑偭偨壓偺寘偺悢乿偱暘椶偡傞偲丄
悢楍偺婯懃乮俋乣侾傪孞傝曉偟巊偆乯傛傝丄師偺俇偮偺僌儖乕僾偵暘偐傟傑偡丗
嵟屻偺寘偑丄俋丆俋俉丆俇丆俇俆丆俁丆俁俀 丒丒丒偙傟傪乽嵟屻偺寘乿偲屇
傇偙偲偵偟傑偡丅
偝偰丄曗戣侾傛傝丄嵟弶偺俁寘偼丄俁偱妱傟傑偡偟丄
埲崀偺俁寘偯偮嬫愗偭偨暘傕偦傟偧傟俁偱妱傟傞偺偱丄
曗戣俀傛傝丄寢嬊乽嵟屻偺寘乿偑俁偱妱傟傞偐偳偆偐偱丄
偦偺悢偑俁偱妱傟傞偐偳偆偐偑妋掕偟傑偡丅
嵟屻偺寘偑俁偱妱傟傞偺偼丄俋丆俇丆俁偺俁偮偺僌儖乕僾偱偡丅
傑偨丄嵟屻偺寘偑側偄傕偺乮俁寘偢偮嬫愗傝偒傟偨傕偺乯偼丄曗戣侾偲曗戣俀傛傝丄
俁偱妱傝愗傟傑偡丅
寢嬊丄嵟屻偺寘偑俋俉丆俇俆丆俁俀偺傕偺埲奜偺乮悢楍拞偺乯
偡傋偰偺悢偼俁偱妱傝愗傟偰偟傑偄傑偡丅
巆偭偨俁偮偺僌儖乕僾偼丄壓侾寘偑嬼悢偲俆側偺偱丄
偄偢傟傕俀偐俆偱妱傝愗傟偰偟傑偄傑偡丅
寢壥丄偙偺拞偵慺悢偼偁傝傑偣傫丅
仈 偁傟丠
[曗戣侾偺徹柧]
俁寘偺悢傪乽ABC乿偲彂偄偨偲偟傑偡丅
BC乿 = A亊100+B亊10+C = A亊99+B亊9+(A+B+C) = 3亊(A亊33+B亊3)+(A+B+C)
A,B,C偺偆偪嵟彫偺悢傪a偲偡傞偲丄偺偙傝偺俀偮偼偦傟偧傟丄
a+1,a+2 偲側傝丄
A+B+C = a+(a+1)+(a+2) = a亊3+3 = 3亊(a+1)
寢嬊丄乽ABC乿 = 3亊(A亊33+B亊3)+3亊(a+1) = 3亊(A亊33+B亊3+a+1) 偲側傝丄俁偱妱傝
愗傟傞丅
[曗戣俀偺徹柧]
偔偭偮偗傞慜偺悢傪A偲偟丄偔偭偮偗偨悢傪B偲偟偰丄B偺寘悢傪倠偲偡傞偲丄
嶌偭偨悢偼丄
A亊10k + B
A傕B傕俁偱妱傝愗傟傞偺偱丄偦傟偧傟 3亊a, 3亊b 偲偍偔偲丄
A亊10k + B = 3亊a亊10k + 3亊b = 3亊(a亊10k+b)偲側傝丄俁偱傢傝偒傟傞丅
仈 彫妛峑偺偙傠丄

乮儁儞僱亅儉丗昹揷丂柧枻乯
楢懕偡傞俁値乮値偼帺慠悢乯屄偺惍悢偺榓偼俁偺攞悢偱偁傞丏
偟偨偑偭偰慺悢偺岓曗偲偟偰丆
偙傟偼侾侽侽侽侽侽侽寘埲壓偺悢楍撪偵慺悢偺岓曗
乮亖婏悢偱偁傝丄俁偺攞悢偱側偔丄俆偺攞悢偱側偄悢乯
偑偁傞偐偳偆偐傪僠僃僢僋偡傞僾儘僌儔儉偱偡丅
Sub sosuu()
Dim max, a(1000000) As Long: max = 1000000
Dim wa, kosuu, j, jj As Integer: wa = 0: kosuu = 0
For j = 1 To max
a(j) = 9 - ((j - 1) Mod 9): wa = (wa + a(j)) Mod 3
If wa > 0 And a(j) Mod 2 = 1 And a(j) <> 5 Then
kosuu = kosuu + 1
For jj = 1 To j: Selection.TypeText Text:=a(jj): Next
Selection.TypeParagraph
End If
Next
If kosuu = 0 Then
Selection.TypeText Text:=Str$(max) + "寘埲壓偺悢偵偼丆慺悢偼偁傝傑偣傫偱偟偨丏"
Selection.TypeParagraph
End If
End Sub
幚峴偟偨寢壥丄
乽 1000000寘埲壓偺悢偵偼丆慺悢偼偁傝傑偣傫偱偟偨丏乿偑昞帵偝傟傑偟偨丅

乮儁儞僱亅儉丗偪傖傔乯
乮摎偊乯丂慺悢偼懚嵼偟側偄丅
乮嘥乯俀偼悢楍偺儊儞僶乕偱偼側偄丅
乮嘦乯侾偺埵偑俀丆係丆俇丆俉偱偁傞丄
悢楍偺儊儞僶乕偼俀偺攞悢偱偁傞偙偲偵傛傝丄
侾偺埵偑俆偱偁傞儊儞僶乕偼俆偺攞悢偱偁傞偙偲偵傛傝丄偦傟偧傟慺
悢偱偼側偄丅
乮嘨乯侾偺埵偑丄侾丆俁丆俈丆俋偺応崌傪峫偊傞丅
乽偁傞帺慠悢偑俁偺攞悢偱偁傞昁梫廫暘忦審偼
偦偺悢偺奺埵偺悢帤偺榓偑俁偺攞悢偱偁傞乿偙偲偼婛抦偲偡傞丅

乮儁儞僱亅儉丗傕偺傕偺乯
嬼悢偍傛傃侾偺埵偑俆偺帺慠悢偼慺悢偱側偄偙偲偼柧傜偐丄
傛偭偰丄侾偺埵偑侾丄俁丄俈丄俋偺応崌偵偮偄偰峫偊傞丅
| 俋俉俈丒丒丒侾俋俉俈丒丒丒侾丒丒丒俋俉俈俇俆係俁俀侾 | |
| 亖 | 俋俉俈俇俆係俁侾亊侾侽a亄俋俉俈俇俆係俁俀侾亊侾侽b亄丒丒丒亄俋俉俈俇俆係俁俀侾 |
| 亖 | 俋俉俈俇俆係俁俀侾亊乮丒丒丒乯丂丂乮奺崁丄俋俉俈俇俆係俁俀侾偑栺悢側偺偱乯 |
| 俋俉俈丒丒丒侾俋俉俈丒丒丒侾丒丒丒俋俉俈俇俆係俁 | |
| 亖 | 俋俉俈俇俆係俁俀侾亊侾侽a亄俋俉俈俇俆係俁俀侾亊侾侽b亄丒丒丒亄俋俉俈俇俆係俁 |
| 亖 | 俁亊乮丒丒丒乯丂丂乮奺崁丄俁偑栺悢側偺偱乯 |
| 俋俉俈丒丒丒侾俋俉俈丒丒丒侾丒丒丒俋俉俈 | |
| 亖 | 俋俉俈俇俆係俁俀侾亊侾侽a亄俋俉俈俇俆係俁俀侾亊侾侽b亄丒丒丒亄俋俉俈 |
| 亖 | 俁亊乮丒丒丒乯丂丂乮奺崁丄俁偑栺悢側偺偱乯 |
| 俋俉俈丒丒丒侾俋俉俈丒丒丒侾丒丒丒俋 | |
| 亖 | 俋俉俈俇俆係俁俀侾亊侾侽a亄俋俉俈俇俆係俁俀侾亊侾侽b亄丒丒丒亄俋 |
| 亖 | 俁亊乮丒丒丒乯丂丂乮奺崁丄俁偑栺悢側偺偱乯 |

乮儁儞僱亅儉丗傑傔乯
偙偺傛偆側柍尷悢楍拞偵慺悢偼側偄丅
亂棟桼亃傑偢丄俋乣俋俉俈俇俆係俁俀侾傑偱偱峫偊偰傒傑偡丅
壓堦寘偑嬼悢偲丄俆偼慺悢偱偼側偄偺偱偺偧偒傑偡丅
巆偭偨偺偼丄俋丄俋俉俈丄俋俉俈俇俆係俁丄俋俉俈俇俆係俁俀侾
偙傟傜偺丄奺埵偺榓傪偲偭偰傒傞偲丄俋丄俀係丄係俀丄係俆
偲側傝丄偄偢傟傕俁偺攞悢偱偁傞偙偲偑傢偐傝傑偡丅
廬偭偰丄俋乣俋俉俈俇俆係俁俀侾偼丄嬼悢偐丄俁偺攞悢偐丄俆偺攞悢偺偄
偢傟偐偱丄寢嬊偙偺拞偵慺悢偼偁傝傑偣傫丅
偝偰丄埲忋偺寢壥丄俋俉俈俇俆係俁俀侾偼俁偺攞悢偱偡偐傜丄
偙傟偵侾侽偺値忔傪偐偗偨傕偺傕俁偺攞悢偱偡丅
偮傑傝丄俋俉俈俇俆係俁俀侾埲崀偺悢楍偼丄忢偵乽仜仜亄俁偺攞悢乿
偲偄偆宍傪帩偭偰偄傞偙偲偵側傝傑偡丅
偙傟埲崀傕丄壓堦寘偑嬼悢偲俆偺悢帤傪偺偧偗偽丄壓偺寘偼
俋丄俋俉俈丄俋俉俈俇俆係俁丄俋俉俈俇俆係俁俀侾
偺偄偢傟偐偱偁傝丄偙傟傜偼偄偢傟傕俁偺攞悢偱偡丅
偙傟偵俁偺攞悢傪壛偊傞傢偗側偺偱丄
偱偒偁偑偭偨悢傕傗偼傝俁偺攞悢偱偁傞偼偢偱偡丅
埲忋偺峫嶡傛傝丄偙偺柍尷悢楍偵偼慺悢偼懚嵼偟傑偣傫丅

乮儁儞僱亅儉丗傆乕乯
傑偢偼俋乣俋俉俈俇俆係俁俀侾傑偱偺侾弰偵偮偄偰丄
俋乮俁偺攞悢乯
俋俉乮嬼悢乯
俋俉俈乮俁偺攞悢乯
俋俉俈俇乮嬼悢乯
俋俉俈俇俆乮俁偺攞悢乯
俋俉俈俇俆係乮嬼悢乯
俋俉俈俇俆係俁乮俁偺攞悢乯
俋俉俈俇俆係俁俀乮嬼悢乯
俋俉俈俇俆係俁俀侾乮俁偺攞悢乯
俀弰栚埲崀偼
丒丒丒俋亖俁偺攞悢亊値亄俋亖俁偺攞悢
丒丒丒俋俉亖嬼悢
丒丒丒俋俉俈亖俁偺攞悢亊値亄俁偺攞悢亖俁偺攞悢
丒丒丒俋俉俈俇亖嬼悢
丒丒丒俋俉俈俇俆亖俁偺攞悢亊値亄俁偺攞悢亖俁偺攞悢
丒丒丒俋俉俈俇俆係亖嬼悢
丒丒丒俋俉俈俇俆係俁亖俁偺攞悢亊値亄俁偺攞悢亖俁偺攞悢
丒丒丒俋俉俈俇俆係俁俀亖嬼悢
丒丒丒俋俉俈俇俆係俁俀侾亖俁偺攞悢亊値亄俁偺攞悢亖俁偺攞悢
偙偺傛偆偵昁偢俀丄傑偨偼丄俁偺攞悢偲側傞偺偱慺悢偼柍偄両両
俁偺攞悢偐偳偆偐傪敾抐偡傞偨傔偺峫偊曽丄
乽奺埵偺悢偺榓偑俁偺攞悢偱偁傟偽傛偄乿傪抦偭偰偄偨偺偱傢偐傝傑偟偨丅

乮儁儞僱亅儉丗Chee乯
偙傟偼丄乽惍悢丗a,b,c偑摍嵎悢楍偵側偭偰偄偰丄
a亊b亊c偑慺悢偵側傞傕偺乿偲偄偆堄枴偱椙偄偺偱偟傚偆偐丠
偦偆夝庍偟偰埲壓恑傒傑偡丅
[夝摎]
慺悢偺栺懇偐傜丄場悢乮偺愨懳抣乯偑侾偲偨偩堦偮偺
慺悢偟偐偁偭偰偼偄偗側偄偺偱丄
a,b,c偺偆偪丄堦偮偩偗偑乮愨懳抣偑乯慺悢偱丄
偁偲偺擇偮偼侾傕偟偔偼亅侾乮愨懳抣偑侾乯丅
愨懳抣偑侾偺傕偺偑丄偳偪傜傕侾乮傑偨偼亅侾乯偩偲丄
摍嵎悢楍偺忦審偐傜俁斣栚偺惍悢傕侾乮傑偨偼亅侾乯偲側傝丄
愊偺寢壥傕侾乮傑偨偼亅侾乯偱丄慺悢偵側傜側偄丅
寢嬊丄a,b,c偼丄乽亅侾丄侾丄乮愨懳抣偑乯偁傞慺悢乿偐傜慖傇偙偲偵側傞丅
亅侾偲侾偺娫偵偼慺悢偑側偄偙偲偲丄亅侾偲侾偺嵎暘偑俀偱偁傞偙偲偵拲堄偡傞偲丄
乽乮愨懳抣偑乯偁傞慺悢乿偲側傞惍悢偼丄亅俁丅
寢嬊媮傔傞悢楍偼丄乽亅俁丄亅侾丄侾乿偱丄愊偼俁丅
仈 偲偙傠偱丄慺悢偭偰偺偼丄俀埲忋偩偲偟偰偄偄傫偱偡傛偹丅

乮儁儞僱亅儉丗偝偩傗傫乯
夝丂丂-a,-1,1
偲偍偔偲丆-1-乮-a乯=1-(-1)亖岞嵎 a:慺悢
側偺偱丆a=3
摎偊丂-3丆-1丆1丂乮傑偨偼1丆-1丆-3乯
姶憐
傁偭偲尒偰丆乽偙傟偼柍棟乿偲偄偆偐丆乽夝側偟乿偲巚偄傑偟偨丅
婥傪偲傝側偟偰峫偊偰傒傑偟偨丅
摍嵎悢楍偲偄偆偙偲偐傜丆丂丂a-d,丂 a,丂a+d
慺悢偲偄偆偙偲偐傜丆丂丂丂丂丂丂1丆1丆a
傆偆傓丅丂丂丂丂丂丂丂丂丂丂丂-1亊0亊1亖0丂?????
偱傕側偄偟丆乧乧乧乧
偁偭丆偦偆偐丅丂丂丂a, -1, 1 丂丂偲偍偔偲丂岞嵎偑2偩偐傜丆a=-3
夝偗偰傒傞偲丆偦傟傎偳擄偟偔側偄傛偆側婥偵側偭偰偟傑偆偐傜晄巚媍丅

乮儁儞僱亅儉丗偪傖傔乯
俁惍悢偺側偡摍嵎悢楍偺岞嵎傪倠乮侽偱側偄惍悢乯偲偟丄
俁偮偺惍悢傪丂n-k, n ,n+k丂 偲偡傞丅
偙偺俁悢偑戣堄傪枮偨偣偽丄n+k, n, n-k 傕戣堄傪枮偨偡偺偱丄k>0
偱峫偊傟偽廫暘丅
s=(n-k)亊n亊(n+k)
倱偑慺悢偲側傞偨傔偵偼丄
乽俁偮偺悢偺偆偪偄偢傟偐俀偮偺愊偺愨懳抣偑侾偱偁傞乿乮仏乯
偙偲偑昁梫偱偁傞丅
丂丂乥(n-k)(n+k)乥=1
傪k>0偱夝偔偲丄(n,k)= (0,1)丅
丂偙偺偲偒s=0偲側傝晄揔丅
丂傛偭偰丄忦審乮仏乯傪枮偨偡偨傔偵偼
丂|n(n-k)|=1傑偨偼 |n(n+k)|=1 偱偁傞偙偲偑昁梫丅丂
丂 |n(n-k)|=1 傪k>0偱夝偔偲丂(n,k)=(1,2)
偙偺偲偒丄丂s=(-1)亊1亊3=-3 偱晄揔丅
丂|n(n+k)|=1傪k>0偱夝偔偲丄(n,k)=(-1,2)
丂偙偺偲偒丄丂s=(-3)亊(-1)亊1=3 偱倱偼慺悢丅
埲忋偐傜丄媮傔傞俁偮偺惍悢偼丄{-3, -1, 1} 丒丒丒丂乮摎偊乯
乮 摍嵎悢楍偺岞嵎傪峫椂偡傞偲丂(-3, -1, 1) 偲丂(1, -1, -3)丂乯

乮儁儞僱亅儉丗寧偺岝乯
弶崁亅俁丄崁嵎俀偺悢楍
-3 ,-1 ,1 嶰偮偐偗傞偲俁乮慺悢乯偵側傞丅
崁偑惍悢偺摍嵎悢楍偱偼偙傟偩偗偺傛偆偵巚偄傑偡丅
暋慺悢偱峫偊傞偲丄弶崁1-ai丄崁嵎ai偺悢楍
1-ai , 1 , 1+ai 偼妡偗傞偲 1+a2偵側傝傑偡丅
偙偺宍偺慺悢偼柍尷偵偁傞偺偱偼側偄偱偟傚偆偐丅

乮儁儞僱亅儉丗彫弔乯
-3,-1,1偺偲偒岞嵎 俀偺摍嵎悢楍傪側偟偰偄傑偡丅

乮儁儞僱亅儉丗ZEN 仌 TUNAKI乯
摍嵎俀偺悢楍偱丄亅俁丄亅侾丄侾偑丄嶰偮偺惍悢偱偡丅

乮儁儞僱亅儉丗悢妝幰乯
亅俁丄亅侾丄侾
愢柧
愨懳抣偑俀埲忋偺悢偑俀偮偁偭偰偼偩傔丅
摉慠侽傕偩傔丅
偟偨偑偭偰丄俁偮偺偆偪偺俀偮偼乕侾偲侾偱偁傞丅
愊偑惓偵側傞偙偲傪峫椂偡傞偲丄傕偆堦偮偺悢偼亅俁偱偁傞丅

乮儁儞僱亅儉丗Y師榊乯
-3 , -1丂,丂1丂
愨懳抣1埲奜偺2惍悢傪偐偗偰惓偺惍悢偵側偭偨応崌
偦偺偳偪傜偺惍悢偺愨懳抣偱傕妱傝愗傟傞偺偱丄慺悢偱偼側偄丅
傑偨丄0偑崿偠傞傕偺偼榑奜丅
傛偭偰丄愨懳抣1埲奜偺惍悢偼2偮埲忋偁偭偰偼側傜側偄丅
偡傞偲丄昁慠揑偵丂-1丄1偑擖傞丅
傛偭偰丄愊偑惓偵側傞傕偺偼丂-3 , -1 , 1

乮儁儞僱亅儉丗偁傝偝偺偍晝偝傫乯
(-3, -1, 1)丂慡晹偐偗偰 3 偵側傝傑偡丅
堦弖丆乽悢傪偐偗崌傢偣偰慺悢偵側傞偼偢偑側偄偱偟傚両丂曄側栤戣両乿
偲巚偄傑偟偨偑丆偡偖偵惍悢偼帺慠悢偠傖側偄偙偲偵婥偯偒傑偟偨丅
梋択丗
巹偺僲乕僩僽僢僋偵擖偭偰偄傞帿彂乮儅僀儁僨傿傾偲偄偆娙堈宆偺昐壢帠揟偱偡丅乯
偵傛傞偲丆
偦偡偆亂慺悢亃
堦偲偦偺悢帺恎偲偺奜偵偼栺悢偑側偄惓偺惍悢丅仈堦偼彍偔丅
傗偔偡偆亂栺悢亃
惍悢(惍幃)俙偑懠偺惍悢(惍幃)俛偱妱傝愗傟傞帪偺丄俙偵懳偡傞俛偺偙偲丅
佁攞悢
偣偄偡偆亂惓悢亃亂惍悢亃
(1) 亂惓悢亃楇傛傝戝偒偄悢丅佁晧悢丅仈positive number偺栿岅丅
(2) 亂惍悢亃楇偍傛傃偦傟偵師師偵堦傪壛偊偨傝堷偄偨傝偟偰摼傜傟傞斖埻偺悢丅
仈integer偺栿岅丅
偙偺掕媊偩偲丆栺悢偼惓偺悢偲偄偆尷掕偑偁傝傑偣傫偺偱丆
1傪彍偔慡偰偺悢 n 偵懳偟偰丆
n = (-n)亊(-1)
偱丆n 偑惍悢側傜 (-n) 傕惍悢偱丆(-n) 偼 n 偱傕 1 偱傕偁傝傑偣傫偐傜丆
慺悢偼偙偺悽偵懚嵼偟側偄偙偲偵側偭偰偟傑偄傑偡丅

| kiyo | 偝偩傗傫 | 偁傝偝偺偍晝偝傫 | 悢妝幰 | 昹揷丂柧枻 |
| 悈偺棳傟 | 傒傗 | Chee | 偪傖傔 | 寧偺岝 |
| 傕偺傕偺 | 彫弔 | 傑傔 | ZEN 仌 TUNAKI | 傆乕 |
| Y師榊 |

栤戣侾偵偮偄偰
慺悢偵偮偄偰偺榖偼
俆丏僇亅僪偺栤戣偱傕偟傑偟偨丅
師偺悢偱妱傝愗傟傞偐偳偆偐傪敾掕偡傞曽朄傪傕偆侾搙帵偟傑偡丅
俀丒丒丒壓侾寘偑嬼悢側傜妱傟傞
俁丒丒丒奺寘偺悢帤傪懌偟偰傒偰偦傟偑俁偱妱傝愗傟傟偽丄妱傟傞丅
係丒丒丒壓俀寘偑係偱妱傝愗傟傟偽妱傟傞
俆丒丒丒壓侾寘偑俆偐侽側傜妱傟傞
俇丒丒丒俀偱妱傟偰丄俁偱妱傟傟偽丄妱傟傞
俈丒丒丒壓偐傜俁寘偛偲偵嬫愗傝丄婏悢斣栚偺傕偺偺榓偲丄嬼悢斣栚偺傕偺偺榓偺嵎偑俈偺攞悢側傜妱傟傞丅
俉丒丒丒壓俁寘偑俉偱妱傝愗傟傟偽妱傟傞
俋丒丒丒奺寘偺悢帤傪懌偟偰傒偰偦傟偑俋偱妱傝愗傟傟偽丄妱傟傞丅
侾侽丒丒丒壓侾寘偑侽側傜妱傟傞(変側偑傜偮傑傜側偄偙偲偐偄偰傞側偁丒丒丒)
侾侾丒丒丒婏悢寘偺榓偲嬼悢寘偺榓偺嵎偑丄侾侾偺攞悢側傜妱傟傞
侾俀丒丒丒係偱妱傟偰丄俁偱妱傟傟偽丄妱傟傞
侾俁丒丒丒壓偐傜俁寘偛偲偵嬫愗傝丄婏悢斣栚偺傕偺偺榓偲丄嬼悢斣栚偺傕偺偺榓偺嵎偑侾俁偺攞悢側傜妱傟傞丅
偙傟偵偮偄偰偺徻偟偄徹柧
偙偺栤戣偺応崌丄乽俋俉俈俇俆係俁俀侾乿偑偳偺埵抲偵偙傛偆偲傕
(亊侾侽値丄値偼擟堄)丄偦傟埲壓偺寘偑俀丆俁丆俆偺攞悢側傜丄尦偺悢傕
俀丆俁丆俆偵側傞偺偱丄傔偱偨偔偡傋偰崌惉悢(慺悢偱側偄傕偺)偲側傝傑偡丅
乽偝偩傗傫乿偝傫偺偍偭偟傖傞捠傝丄慺悢偑傒偮偐傝偩偡偲戝曄偐傕偟傟傑偣傫丅
戝偒側悢偵側偭偨偲偒偵丄偦偺悢俶偑慺悢偐斲偐丄敾掕偡傞偨傔偺曽朄偼偙傟偲偄偭偰側偄偐傜偱偡丅
巇曽側偄偱偡偐傜丄俀丄俁丄俆丄俈丄侾侾丄侾俁丄侾俈丒丒丒偲慺悢偱弴斣偵妱偭偰偄偭偰俶偺栺悢傪扵偡偟偐側偄偱偟傚偆丅
偦傟傪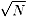 傑偱孞傝曉偟偰尒偮偐傜側偗傟偽俶偼慺悢偱偡丅
傑偱孞傝曉偟偰尒偮偐傜側偗傟偽俶偼慺悢偱偡丅
側偤丄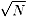 傑偱扵偣偽廩暘側偺偱偟傚偆偐丠丂
傑偱扵偣偽廩暘側偺偱偟傚偆偐丠丂
栺悢偼昁偢儁傾偑偄傞偐傜偱偡丅傕偟丄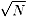 傪墇偊偨偲偙傠偵栺悢偑傒偮偐偭偨側傜
幚偼偦偺僷亅僩僫亅偑
傪墇偊偨偲偙傠偵栺悢偑傒偮偐偭偨側傜
幚偼偦偺僷亅僩僫亅偑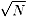 傛傝慜偵偄偨偼偢偱偡傛偹丅
偩偐傜
傛傝慜偵偄偨偼偢偱偡傛偹丅
偩偐傜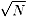 傑偱偱廩暘側偺偱偡丅
傑偱偱廩暘側偺偱偡丅
栤戣俀偵偮偄偰
乽偐偗偰慺悢丠乿偲偄偆偙偲偱丄偁傟偭丠丂偲巚偭偨曽傕偄傞偐偲巚偄傑偡丅
巹傕偦偺侾恖偱偡丅偦傟偑偍傕偟傠偔偰弌戣偟偰傒傑偟偨丅
乽Chee乿偝傫偺僐儊儞僩偵偁傞乽侾偼慺悢偐丠乿偲偄偆揰偱偡偑丄
乽侾偼慺悢偱偼側偄乿偲偄偺偑寢榑偱偡丅
傕偟偐偟偨傜丄乽侾傕慺悢乿偲偡傞偲偄偆棫応偱榑棟傪揥奐偡傞偙偲傕偱偒傞偺偐傕偟傟傑偣傫偑丒丒丒丅
偱偼側偤侾傪慺悢偲偟側偄偺偱偟傚偆偐丠
偦傟偼侾埲奜偺惓偺惍悢(帺慠悢)偺慺場悢暘夝偺堦堄惈傪曐徹偡傞偨傔偱偡丅
| 慺場悢暘夝偺堦堄惈 侾偱側偄惓偺惍悢偼丄慺悢偺愊偲偟偰丄堦堄揑偵偐偗傞丅 |
偲偄偆傕偺偱偡丅
椺偊偽丄侾俀亖俀亊俀亊俁偲慺場悢暘夝偝傟傑偡丅
偙傟偼偐偗傞弴斣傪峫椂偟側偗傟偽偨偩侾捠傝偺暘夝偵側傝傑偡丅
偲偙傠偑丄侾傕慺悢偲偄偆偙偲偵偟偰偟傑偆偲丄
侾俀亖侾亊俀亊俀亊俁
侾俀亖侾亊侾亊俀亊俀亊俁
丒丒丒側偳偄偔傜偱傕丄暘夝偺曽朄偑偁傞偙偲偵側偭偰偟傑偆偐傜偱偡丅
乽慺悢乿偲偄偆柤徧偼傛偔偮偗偨傕偺偩側偁偲巚偆偺偱偡偑丄悢(帺慠悢)偺乽慺乿偵側偭偰偄傞丄
偦傟傜偵昁偢暘夝偱偒傞丄偦偙偵偼侾傪擖傟側偄曽偑帺慠丄偲偄偆傢偗偱偡偹丅
傑偨惍悢榑偵尷傜偢丄偙偺慺場悢暘夝偺堦堄惈偑掕棟偺徹柧側偳偵
廳梫側栶妱傪壥偨偟偰偄傞応柺偑偁傝傑偡丅
偲偙傠偱丄慺悢偵傑偮傢傞榖傪傕偆侾偮丅
崌惉悢偑楢懕俆屄懕偄偰偄傞偲偙傠傪尒偮偗傜傟傑偡偐丠
崌惉悢偑楢懕侾侽侽屄懕偄偰偄傞偲偙傠傪尒偮偗傜傟傑偡偐丠
嵟弶偵尰傟傞丄崌惉悢楢懕俆屄偼丄乷俀係丆俀俆丆俀俇丆俀俈丆俀俉乸偱偡丅
偙傟偼斾妑揑娙扨偵尒偮偗傞偙偲偩偱偒傑偡丅
偱偼楢懕侾侽侽屄偼偳偆偱偟傚偆丠
侾侽侾両亄俀丄侾侽侾両亄俁丄丒丒丒丄侾侽侾両亄侾侽侾偲偄偆楢懕偟偨侾侽侽屄偺惍悢傪峫偊傑偡丅
嵟弶偵偁傞侾侽侾両亄俀偼俀偱妱傝愗傟傑偡偐傜俀偺攞悢偱偡丅
俀斣栚偺侾侽侾両亄俁偼俁偱妱傝愗傟傑偡偐傜俁偺攞悢偱偡丅
丂丂丂丒丒丒丂
嵟屻偵侾侽侾両亄侾侽侾偼侾侽侾偱妱傝愗傟傑偡偐傜侾侽侾偺攞悢偱偡丅
偲偄偆傢偗偱丄偙傟傜偼侾侽侽屄偺楢懕偟偨崌惉悢偲側傝傑偡丅
偟偐偟側偑傜丄偙傟偑楢懕侾侽侽屄偺崌惉悢偲偟偰丄嵟彫偺傕偺偐偳偆偐偼傢偐傝傑偣傫丅
偨偩丄懚嵼偼帵偟偨偲偄偆偩偗偱偡丅
摨條偵嶌傟偽偄偄傢偗偱偡偐傜丄
幚偼擟堄偺俶偵懳偟偰丄崌惉悢楢懕俶屄偲偄偆偺傪尒偄偩偡偙偲偑偱偒傑偡丅
偨偩偟偛憐憸偺捠傝丄偦傟偼偲偰偮傕側偔戝偒偄悢偵側傞偱偟傚偆丅
慺悢偲偄偆偺偼丄傑偩傑偩傢偐偭偰偄側偄偙偲傕懡偔丄杮摉偵枺椡揑側懚嵼偱偡丅
 栠傞
栠傞