Weekend Mathematics／問題／問題32

３２．楕円の問題

  1. 道路にトンネルがあります。 このトンネルのア−チは各車線に半楕円形にあり、 高さは幅と同じです。 あるトラックの幅は６フィ−トで、高さは１２フィ−トです。 このトラックが通ることのできる最も低いトンネルの高さはどれくらいでしょうか？ (一部、表現を変えてあります。)

  2. あるビリヤ−ド台は長軸が短軸よりも２フィ−ト長い楕円形をしています。 一方の焦点から球が突かれ、２回のクッションの後、はじめの位置に戻ってきました。 その道筋の中間では、球ははじめの位置から８フィ−ト離れていました。 台の大きさはどれだけでしょうか？



問題の出典


悩め！パスラ−(挑戦その１)

アンジェラ・フォックス・ダン編

啓学出版






答えと解説












答えと解説

問題１


解答・その１

（ペンネ−ム：ありさのお父さん）

答え：約１３．４フィート
これは高さを半分に縮めて考えると、楕円が円になり、 問題文が次のようになります。

道路にトンネルがあります。 このトンネルのア−チは各車線に半円形にあり、 高さは幅の半分です。 あるトラックの幅は６フィ−トで、高さは６フィ−トです。 このトラックが通ることのできる最も低いトンネルの高さはどれくらいでしょうか？

円の中心（トラックの底面の真ん中）から、 トラックの屋根の端までの距離は、横に３フィート、 上に６フィートなので、
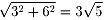
これが、トンネルの高さと同じです。
元の問題に戻るには、高さを２倍にすればいいので、 答えは 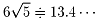ですね。
もちろん、Ｆ１ドライバー以上の運転テクニックがないと壁にぶつかりますが。



解答・その２

（ペンネ−ム：ちゃめ）

以下、数字の単位はフィートとする。
題意から、トンネルのアーチの半楕円は、長軸の長さ２ａ、 短軸の長さａの楕円を短軸で切った形である。
トラックを幅６、高さ１２の長方形とみなす。
最小のトンネルは、６×２４の長方形を２４の辺を長軸方向に置いたときに 長方形が内接する楕円を短軸で切ったきさである。
長方形が内接した楕円を長軸方向を１／２に縮小すると、６×１２の長方形が 内接した半径ａ／２の円になる。
長方形の対角線の長さ＝円の直径、だから、 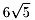＝a。
求める高さは2a/2＝a＝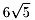
（答え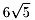）　フィート




解答・その３

（ペンネ−ム：水の流れ）

楕円の方程式を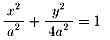とおく。 （ただし、ａ＞０）

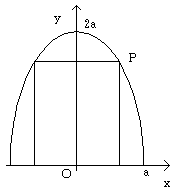
楕円周上の点Ｐ(ａ cosθ,２ａ sinθ)とおくと、幅が６フィ−ト、高さが１２フィ−トより、
ａ cosθ＝３,２ａ sinθ＝１２とできる。
cosθ＝３／ａ,sinθ＝６／ａより、cos2θ＋sin2θ＝１に代入して、 (６／ａ)2＋(３／ａ)2＝１
４５＝ａ2、ａ＞０より　ａ＝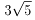
トンネルの高さは、2a=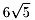(フィ−ト)・・・答





解答・その４

（ペンネ−ム：かねさん）

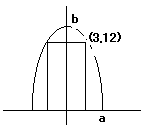
求める楕円の式を 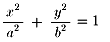　 , b=2a とおく。
トラックの右上の座標を (3,12) として上式に代入し， 整理すると，a=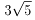となる。
このとき，トンネルの高さ b=2a=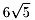

(図：mon321.gif)



解答・その５

（ペンネ−ム：ものもの）

まず、楕円の方程式を 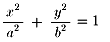　 、b>a>0 とします 幅と高さが同じなので 2a=bとなります
代入して　 4x2+y2=4a2 となります
トラックが幅6、高さ12で、真ん中を通るのが最適らしいので,(x,y)=(3,12)を通 るとします
これを代入して 36+144=4a2
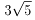よって a=、　 b=2a=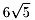
トンネルの高さはb＋hフィート。hは微小量



解答・その６

（ペンネ−ム：浜田　明巳）

トンネルの高さをｈフィート（ｈ＞０）とすると，アーチの断面の方程式は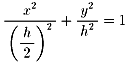， （ｙ≧０）となります．
この半楕円上に点(±３,１２)があればよいので，この点の座標を代入すると，

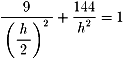
∴ｈ2＝１８０
∴ｈ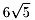＝（フィート） （＝１３.４１６……）
これが高さとなります．ただしこれではあまりにもぎりぎりであるので， １３.４２フィート くらいが妥当かも知れません．
トラックやトンネルが傷ついてしまいますから．



解答・その７

（ペンネ−ム：数楽者）

高さ方向を半分に縮めると円になります。
高さを半分にしたトラックの大きさから、 中心から（３，６）の所に円周があります。
中心からそこまでの距離は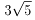です。
したがって、もとのトンネルの高さは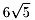です。 （単位は省略しました)



問題２


解答・その１

（ペンネ−ム：ありさのお父さん）

答え：15フィート×17フィート
ご存じの様に、私は中学以降の数学をほとんど忘れてしまっているので、 楕円、長軸、短軸の定義から調べ直しました。マイペディアによると、

楕円
だえん、長円とも。 平面上で二定点(焦点)F，F′からの距離の和が一定な点の軌跡。
F，F′を通る直線をx軸，FF′の垂直二等分線をy軸とする直交座標軸に関し 方程式　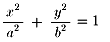　で表わされる。
x軸，y軸の楕円で切りとられた部分を長軸，短軸といい， 両方を主軸という。
面積πab，離心率　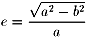 　は1より小さく， 準線は　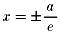　 ⇒円錐曲線の一つ。
二焦点が重なった特別な場合が⇒円。 とありました。

「二焦点からの距離の和が一定」が使えますね。
あと、「焦点から出た光が、楕円面の鏡で反射すると、もう一方の焦点を通る」も、 知識としては覚えています。
（ちなみに、１０年ほど前に、この原理を使った測定装 置の特許アイデアを書いたことがあります。 残念ながら、同じアイデアは先に出ていて特許にはなりませんでしたが。）
でも、今の私には、どちらも証明も式で示すこともできませんので、 気持ち悪いですね。
さて、以下は、上記の「知識」を使った答えです。
「焦点から出た光が、楕円面の鏡で反射すると、もう一方の焦点を通る」と、「二 焦点からの距離の和が一定」から、道筋の中間はもう一方の焦点であることが分かり ます。
あとは、短軸の半分をa、長軸の半分をb、二焦点からの距離の和をrとおくと、
a2+ 42 = (r/2)2
r = 2b
b = a+1 から
a2 + 42 = (a+1)2
∴ a = 15/2
∴ b = 17/2
したがって、台の大きさは、15フィート×17フィート

約５メートルとは、ずいぶん大きいなあ。 日本の家には入りませんね。 間違えたかな？



解答・その２

（ペンネ−ム：ちゃめ）

(一部、表記ミスがありました。ごめんなさい。Junko　9/15)

まず、次の命題を証明する。

[命題１]
「楕円のひとつの焦点から打ち出された球は、１回目の反射と２回目の反射の途中で もう一方の焦点を通る。」


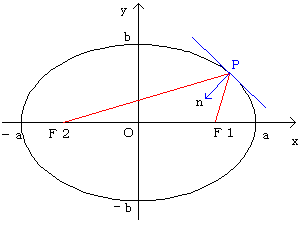
楕円E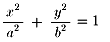：　　(a>b>0)の焦点は


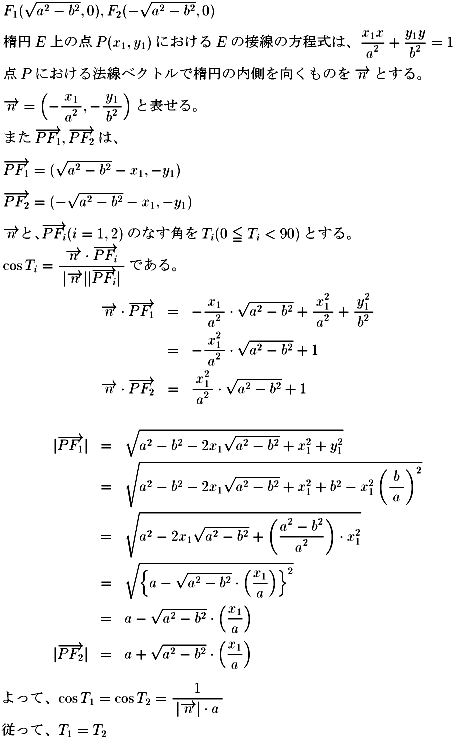
このことは、F1から打ち出されPにT1の角度で入射した球はT2の方向に 反射されることを示す。 すなわち、Ｐで反射された球は次に反射するまでにF2を通る。逆もまたなりたつ。 よって命題１が証明された。
焦点F1から打ち出された球がまず点P1で反射し、 もう一つの焦点F2を通ってから点P2 で反射しF1に戻るとする。
楕円の性質より、F1P1+P1F2 = F2P2+P2F1 だから、 F1->P1->F2->P2->F1の経路の中間 点はF2である。
以上から、問題の台の楕円の焦点間の長さが８フィートであることが解る。 この楕円の長軸の長さを2ｌとすると、


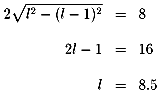
従って求める台は、 長軸の長さ１７フィート、短軸の長さ１５フィートの楕円　・・・　（答え）
２の答えはずいぶん大きな台になってしまったみたいです。 ビリヤードはやったこと がないので実際どのくらいの大きさの台を使うのか知らないのですが。
命題１の証明をしてみて、焦点という言葉の意味をあらためて納得しました。



解答・その３

（ペンネ−ム：水の流れ）

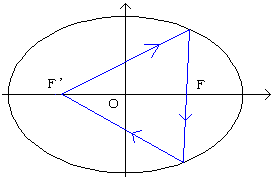
楕円の長軸を２ａ(フィート)、短軸を２(ａ−１)(フィート)とおく。
２焦点の座標を(±ｃ,０)とする。ただし、ｃ＞０

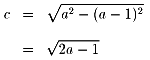
一方、焦点から出た球は他の焦点を通ることより、 中間での位置が８フィートということは２焦点ＦＦ’ということです。
２ｃ＝８より、

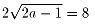
ａ＝１７／２
よって、長軸１７フィート，短軸１５フィートの楕円の大きさである。




解答・その４

（ペンネ−ム：かねさん）

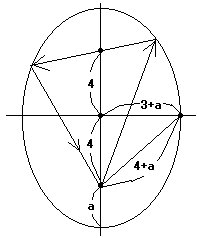
焦点から出発し，１回目のクッション後もうひとつの焦点を 通過する。その後２回目のクッション後もとの位置に戻る。
中間地点は最初の焦点を出発してクッション後，もうひとつの 焦点を通過するときなので，焦点間の距離が８フィートとなる。
ここで，長軸の長さの半分を４＋ａとおくと，短軸は長軸 より２フィート短いので，短軸の長さの半分は３＋ａ。
ここで，(4+a)2 = 42 + (3+a)2 となり，これを解いて a=9/2
よって，長軸１７フィート，短軸１５フィートの大きさの台。
(図：mon322.gif)



解答・その５

（ペンネ−ム：ものもの）

楕円の方程式を 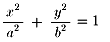　,a>b>0　とする,
楕円の性質として、焦点から真っ直ぐ打ち出されたものは、一回跳ね返って、も う一方の焦点へ到達するらしい
それと楕円の定義から、2回跳ね返って元の焦点に戻る玉の道筋の中間は、もう 一方の焦点となる
よって焦点の間の距離が8となる
焦点が(4,0)なので 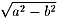＝４
a2-b2=16
長軸が短軸より2長いので 2a=2b+2
a=b+1
1に代入して 2b=15
2a=2b+2=17
よって 台の大きさは長軸が17,短軸が15フィート。



解答・その６

（ペンネ−ム：浜田　明巳）

いつものようにパソコンを使って解いてみました．
長軸，短軸の長さをそれぞれ２ｐ，２(ｐ−１)（ｐ＞１）としますと， 焦点の座標は，Ｆ(ｆ,０)，Ｆ'(−ｆ,０)（ｆ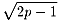＝）となります．
Ｆを出発して，Ｐ1(ｘ1,ｙ1)， Ｐ2(ｘ2,ｙ2)，Ｆに戻るとします． 楕円の性質から，Ｐ1Ｐ2はＦ'を通り， Ｐ2からはねかえってＦに戻るのは明らかです． ＦＰ1の角度を０°から(１８０−０.５)°まで０.５°きざみ （のちにもっと細かく設定します）で考え， それぞれの場合のＰ1，Ｐ2の座標を計算します． 折れ線ＦＰ1Ｐ2Ｆの中点(ｘ3,ｙ3)を求め， その点とＦとの距離を求めます． その距離が８に一番近いｐを求め，それを答とします．

今回はＱＢＡＳＩＣでプログラムを作ってみました． このソフトでプログラムを作るのが一番楽です．
このプログラムにより，答はｐ＝８.５，すなわち， 長軸，短軸の長さがそれぞれ１７，１５となればよいことが分かります．
またＶＩＳＵＡＬ　ＢＡＳＩＣに移植して，実際の図を描いたところ， 折れ線ＦＰ1Ｐ2Ｆの中点は常にＦ'であることが分かりました．
考えてみれば，楕円の定義から，
　ＦＰ1＋Ｐ1Ｆ'＝Ｆ'Ｐ2＋Ｐ2Ｆ
であり，したがって中点がＦ'であることは明らかでした．
故にＦＦ'＝８となればよいので，２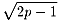＝８ 　∴２Ｐ＝１７
これが答となります．
このように，パソコンで正確な図を描いてみると，答が見えてくることがよくあります．

　　　　　　　　　　　　 

ＱＢＡＳＩＣのプログラム
'daen32.bas
CLS : DEFDBL A-Z: dankai = 6: DIM x(1), y(1), d(1), kizami1(6), kizami2(6)
kizami1(1) = .1: kizami2(1) = .5
FOR j = 2 TO dankai
 kizami1(j) = kizami1(j - 1) * .1: kizami2(j) = kizami2(j - 1) * .2
NEXT
w = 3.14159265359# / 180: min = 100
rangepmin = 1 + kizami1(1): rangepmax = 20
rangetmin = 0: rangetmax = 180 - kizami2(1)
FOR i = 1 TO dankai
 IF i > 1 THEN
  rangepmin = pmin - kizami1(i - 1)
  IF rangepmin < 1 + kizami1(1) THEN rangepmin = 1 + kizami1(1)
  rangepmax = pmin + kizami1(i - 1)
  rangetmin = tmin - kizami2(i - 1)
  IF rangetmin < 0 THEN rangetmin = 0
  rangetmax = tmin + kizami2(i - 1)
  IF rangetmax > 180 - kizami2(1) THEN rangetmax = 180 - kizami2(1)
 END IF
 LOCATE 1, 1
 PRINT USING "p :##.######  t :##.#####  step"; kizami1(i); kizami2(i)
 FOR p = rangepmin TO rangepmax STEP kizami1(i)
  f = SQR(2 * p - 1)
  FOR t = rangetmin TO rangetmax STEP kizami2(i)
   IF t <> 90 THEN
    a1 = TAN(t * w): b1 = -f * a1
    aa = 1 / p / p + a1 * a1 / (p - 1) / (p - 1)
    bbd = a1 * b1 / (p - 1) / (p - 1): cc = b1 * b1 / (p - 1) / (p - 1) - 1
    dd = bbd * bbd - aa * cc
    x1 = (-bbd + (1 + 2 * (t > 90)) * SQR(dd)) / aa: y1 = a1 * x1 + b1
   ELSE
    x1 = f: y1 = (p - 1) * SQR(1 - x1 * x1 / p / p)
   END IF
   d1 = SQR((x1 - f) * (x1 - f) + y1 * y1)
   IF x1 <> -f THEN
    a2 = y1 / (x1 + f): b2 = f * a2
    aa = 1 / p / p + a2 * a2 / (p - 1) / (p - 1)
    bbd = a2 * b2 / (p - 1) / (p - 1): cc = b2 * b2 / (p - 1) / (p - 1) - 1
    dd = bbd * bbd - aa * cc
    FOR j = 0 TO 1
     x(j) = (-bbd + (1 - 2 * j) * SQR(dd)) / aa: y(j) = a2 * x(j) + b2
     d(j) = SQR((x(j) - x1) * (x(j) - x1) + (y(j) - y1) * (y(j) - y1))
    NEXT
    j = -(d(0) < d(1)): x2 = x(j): y2 = y(j): d2 = d(j)
   ELSE
    x2 = x1: y2 = -y1: d2 = 2 * y1
   END IF
   d3 = SQR((x2 - f) * (x2 - f) + y2 * y2)
   l = d1 + d2 + d3: l2 = l * .5
   IF d1 >= l2 THEN
    IF t <> 90 THEN
     x3 = ((d1 - l2) * f + l2 * x1) / d1: y3 = a1 * x3 + b1
    ELSE
     x3 = f: y3 = ((d1 - l2) * 0 + l2 * y1) / d1
    END IF
   ELSEIF d1 + d2 >= l2 THEN
    ll = l2 - d1
    IF x1 <> x2 THEN
     x3 = ((d2 - ll) * x1 + ll * x2) / d2: y3 = a2 * x3 + b2
    ELSE
     x3 = x1: y3 = ((d2 - ll) * y1 + ll * y2) / d2
    END IF
   ELSE
    ll = l2 - d1 - d2
    IF x2 <> f THEN
     x3 = ((d3 - ll) * x2 + ll * f) / d3
     y3 = (0 - y2) / (f - x2) * (x3 - f)
    ELSE
     x3 = f: y3 = ((d3 - ll) * y2 + ll * 0) / d3
    END IF
   END IF
   d = SQR((x3 - f) * (x3 - f) + y3 * y3)
   sa = ABS(d - 8): IF sa < min THEN min = sa: pmin = p: tmin = t
   LOCATE 2, 1
   PRINT USING "at present p=###.######, t=####.#####, sa=###.############"; p; t; sa
   PRINT USING "minimum    p=###.######, t=####.#####, sa=###.############"; pmin; tmin; min
NEXT: NEXT: NEXT: END




解答・その７

（ペンネ−ム：数楽者）

問題文から、楕円の中心から焦点までの距離は４です。
短軸の半分の長さをａ、長軸の半分の長さをｂとすると、
ｂ＝ａ＋１
ｂ２−ａ２＝１６となり、
これを解いてａ＝７．５、ｂ＝８．５となります。
短軸が１５長軸が１７の楕円で、面積は ２５５×π／４です。



正解者

ありさのお父さんちゃめ水の流れ
かねさんものもの浜田　明巳
数楽者





まとめ

今年の夏のサングラスの流行はoval形、つまり楕円形ということだそうで、 何の関係もないのですが、今月は楕円の問題にしました。


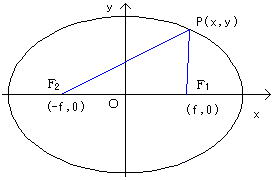
まずは楕円の定義から・・・。

２定点Ｆ１、Ｆ２からの距離の和が一定である点の軌跡を楕円といい、 定点Ｆ１、Ｆ２を焦点といいます。
（楕円の授業をするときにボ−ル紙に２ヶ所穴をあけてひもを通し、楕円を描いて見せたことがあります。）
左図のように２定点をｘ軸上に、２定点の中点が原点になるように配置します。
Ｆ１(ｆ、０)、Ｆ２(−ｆ、０)とします。
ひもの長さをｌ(一定)とします。ただし、ｌ＞２ｆ　
こうすることで、２定点からの距離の和が一定にできるからです。
点Ｐ(ｘ、ｙ)の軌跡を求めてみます。


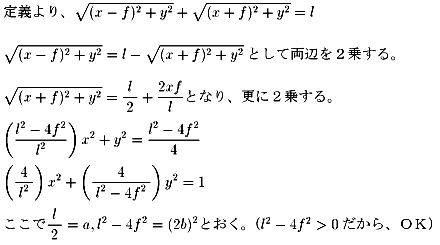
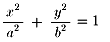となり、これを楕円の標準形といいます。
逆に標準形から、ｌ＝２ａ(これは、点Ｐをｘ軸上においてみればすぐわかります。)
ｆ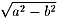＝となります。



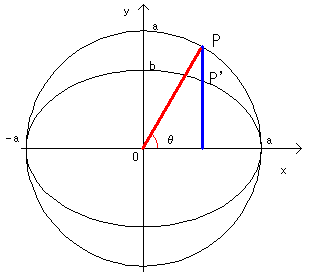
また楕円は、円をｘ軸(or ｙ軸)方向に拡大、縮小したものとしてとらえることもできます。
左の図は、半径aの円とそれをｙ軸方向に(b/a)倍してできる楕円とをかいてものです。
図のようにｙ軸に平行な直線と円、楕円との交点をそれぞれＰ、Ｐ’とするならば、 これらはｘ座標は等しく、ｙ座標については、a:b　になっていることがわかります。
円のパラメ−タ−(媒介変数)表示として知られています、
ｘ＝ａ cosθ 、ｙ＝ａ sinθ　に対して
楕円のパラメ−タ−(媒介変数)表示は、ｙ座標を(b/a)倍して、
ｘ＝ａ cosθ 、ｙ＝ｂ sinθ　で与えられます。

逆に楕円の長軸と短軸が等しいときが円だという風にとらえることもできます。

問題１について

標準形を使った解法が一般的かなあと思いますが、 円との関係を用いて解く方法には感心しました。
(「ありさのお父さん」、「ちゃめ」さん、「数楽者」さん)
円は最も基本的な図形で扱いが容易です。 それを拡大、縮小して楕円になるということはわかっていても、実際に問題を解く段に それを活用するのは、発想が柔軟でないとできないですね。

問題２について


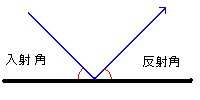
物体が平面に当たると、左図のように 「入射角＝反射角」で跳ね返ることが知られています。
確か物理で勉強しましたよね？


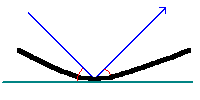
曲面に当たったときはどうなるか？
それは接平面に対して、「入射角＝反射角」で反射するのです。


楕円上の任意の点Ｐをとり、 ２つの焦点と結ぶと、これら２つの線分は接線と等しい角をなすという性質があります。
これについては、「ちゃめ」さんが「解答・その２」で証明をしてくださいました。
(おかげさまで最近私は随分と楽をさせてもらっています、感謝！)
従って、楕円のひとつの焦点から打ち出された球は、どの方向に打ち出されたとしても楕円で反射し、 もう一方の焦点を通ることになります。

仮に左の楕円をｘ軸で回転させて、楕円球(？)のようなものを作り、 焦点に一方に光源をおくと、そこから出た光はすべて楕円面で反射し、 もう一方の焦点に集まるのでしょう。 実際に実験してみたくなりますね？


最後に２次曲線のまとめをします。
ｘ、ｙについての２次方程式　ａｘ２＋ｂｘｙ＋ｃｙ２＋ｄｘ＋ｅｙ＋ｆ＝０は、
楕円(円を含む)、放物線、双曲線、相交わる２つの直線のいずれかになります。
このことから２つの直線を除き(除かない立場もあります)、楕円(円を含む)、放物線、双曲線を２次曲線と呼ぶわけです。


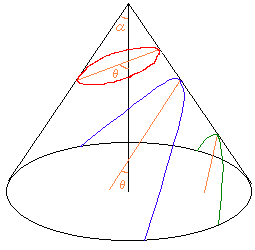
また２次曲線は、別名「円錐曲線」とも呼ばれます。
円錐を頂点を通らない平面で切ったときに現れる曲線だからです。
(頂点を通るような平面できると２つの直線になります。)
円錐の頂点から底面におろした垂線と母線とのなす角をα、 切った平面とのなす角をθとします。

手元に電球スタンドか懐中電灯(防災の日に点検します？)があれば、 それに円錐形のかさをつけて壁に光りを当ててみる、その角度によって 円錐曲線を見ることができるかな・・・？



さて今月のテ−マは楕円ということですが、楕円はサングラスのデザイン以上に 私たちに身近（？）なものです。
なぜなら私たち自身が常に楕円軌道上にいるからです。？？？(実感はないのですけれどね！)
地球も含めて太陽系にある惑星はすべて太陽を１つの焦点として楕円軌道を 描いています。(ケプラーの第1法則)
もっとも地球の描く楕円軌道の離心率　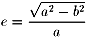は 0.02ですからほぼ円に等しいと考えていいのでしょうね。
もし地球の描く楕円軌道の離心率がもっと大きかったら、 春夏秋冬以上に気候の変動が激しいことになりますね。 太陽に近いところにいる時期と離れたところにいる時期のギャップが激しいわけですから・・・。 そうだとしたら人類は誕生していなかったかも・・・？　なんてことを考えたりします。
地球以外の惑星で一番離心率の小さいものは金星および海王星の0.01、 大きいものは冥王星の0.25です。
(「Microsoft Encarta97 Encyclopedia」による)
一方、太陽系の中でも彗星の離心率たるやすごいだろうなあと思うのです。
「Microsoft Encarta97 Encyclopedia」で調べてみましたら、 ７６年周期で有名なハリ−彗星の離心率が0.967、 １３．５年周期のタトル彗星の離心率が0.824・・・と軒並み高い数値が並んでいました。
いずれにせよ、皆楕円軌道を描いているのですよね。不思議といえば不思議・・・。


最後にＥ・Ｔ・ベル著、東京図書の「数学をつくった人びと」から引用します。

アポロニウスとその後継者によってある程度完全に研究された円錐曲線の幾何学は、 １７世紀以降の天体力学にとって非常に重要なものとなった。 実際、もしギリシャの幾何学者がケプラ−の先駆をつとめなかったら、 面倒で精巧なケプラ−の遊星の軌道に関する計算も、またそれによって準備された ニュ−トンの万有引力の法則も発見されなかったかもしれない。




E-mail 戻る ホ−ムペ−ジ