図の斜線部分の面積を求めてください。
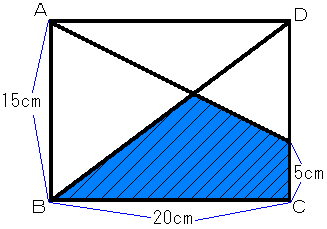
（１）四角形ＡＢＣＤは長方形とします。
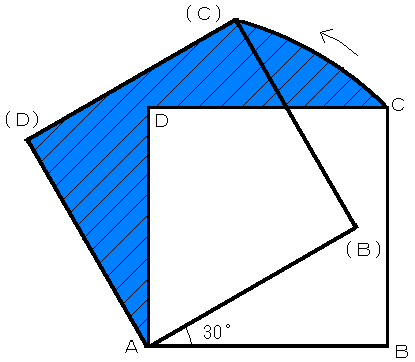
（２）四角形ＡＢＣＤは面積５０cm2の正方形です。
点Ａを中心をして正方形を図のように３０ﾟ回転させました。
Weekend Mathematics／問題／問題67
６７．面積を求める問題
図の斜線部分の面積を求めてください。
（１）四角形ＡＢＣＤは長方形とします。
（２）四角形ＡＢＣＤは面積５０cm2の正方形です。 点Ａを中心をして正方形を図のように３０ﾟ回転させました。
ピーター先生と中学入試の算数に挑戦！
ピーター・フランクル
新潮社
広島女学院中学校2001年度入試
（ペンネ−ム：岡田）
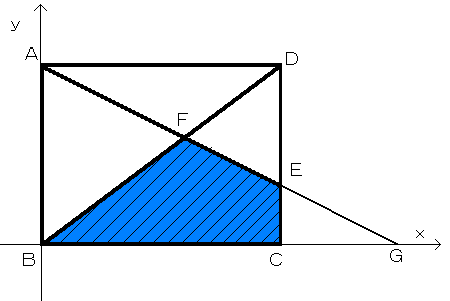
（１）まず点Bを原点として直線BCをx軸、直線BAをy軸とする。
次にCD間にあるAからの直線の交点をEとする。
またBDとAEとの交点をFとする。
また直線AEと直線BCを伸ばしていったところの交点をGとする。
次に直線BDと直線AEの１次関数の式を求める。
直線BDがy=3/4x
直線AEがy=-1/2x+15
これより、直線AEの式からyが０のときにGの値がでる。
0=-1/2x+15
x=30
また直線AE、直線BCの式から交点Fの値も出てくる。
3/4x=-1/2x+15
（ｘ、ｙ）=（12、9）
これより、三角形BFG-三角形CEGをすれば四角形ABCDの面積がでる。
（30*9*1/2）-（10*5*1/2）=110
よって四角形ABCDの面積は110cm2となる。
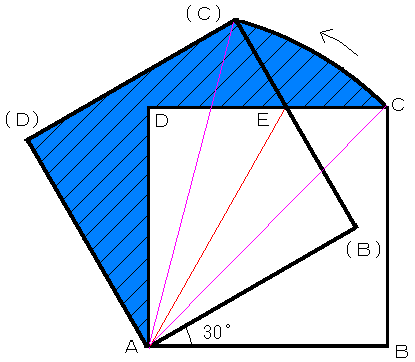
（２）(B)(C)とCDとの交点をEとする。
斜線部分の面積を求めるには、
50-四角形ADE(B)+AC2*π*角CA(C)/360-四角形ACE(C)とできる。
三角形AEDと三角形A(B)Eで、
∠ADE=∠A(B)E=90°
AE=AE （共通）
AD=A(B) （正方形の1辺は等しいから）
これより直角三角形の斜辺と他の1辺がそれぞれ等しいので合同。
次に三角形AECと三角形AE(C)で、
AE=AE （共通）
AC=A(C) （半径が共通）
∠EAC=∠EA(C) （三角形AED≡三角形A(B)Eより）
これより2辺とその間の角がそれぞれ等しいので合同。
これから三角形AED+三角形A(B)E=DE*AD、三角形AEC+三角形AE(C)=EC*AD
よって四角形ADE(B)+四角形ACE(C)=50cm2となる。
次に正方形の面積が50cm2より1辺の長さが5√2ということが分かる。
三平方の定理より、2（5√2）2=102 となりAC=10cm2となる。
∠CABは∠CABの1/2なので45°となる。
また∠DE(B)=120°ということが分かるので、∠（C)EC=240°がでる。
よって∠（C）AC=30°となり（C）ACの扇形の面積は
102*π*30/360=25/3π
これより斜線部分の面積は
50-50+25/3π=25/3π
となり、よって斜線部の面積は25/3πcm2。
（ペンネ−ム：meira）
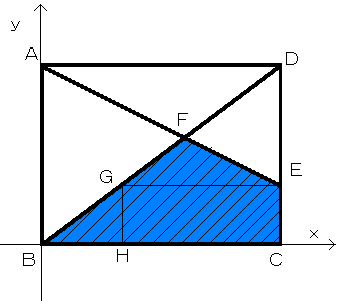
（１）の解答
まず、長方形ＡＢＣＤで、Ｂを原点とし、点Ｂから点Ｃ方向を＋ｘ軸、
点Ｂから点Ａ方向を＋ｙ軸となる座標を設定します。
点Ａから直線ＣＤへ引かれた直線の直線ＣＤとの交点をＥ、直線ＡＥ、ＢＤの交点を
Ｆ、点Ｅからｘ軸と平行な直線を−ｘ軸方向へ引き対角線ＢＤとの交点をＧ、
点Ｇからｙ軸と平行な直線を
−ｙ軸方向へ引き直線ＢＣとの交点をＨとします。
各々の点の座標を求めると、
Ａ（０，１５）、Ｂ（０，０）、Ｃ（２０，０）、Ｄ（２０，１５）、Ｅ（２０，５）で、
直線ＢＤ：ｆ（ｘ）＝(３/４)ｘ ……(1)だから、点Ｇの座標は
Ｇ（(４/３)ｙ、５）＝（(２０/３)、５）
点Ｇの座標から点Ｈの座標は、Ｈ（(２０/３)、０））になります。
直線ＡＥ：ｇ（ｘ）＝−(１/２)ｘ＋１５ ……(2)だから、
(1)と(2)を連立方程式として解くと交点Ｆが求まります。
(1)を(2)に代入すると、
(３/４)ｘ＝−(１/２)ｘ＋１５
(５/４)ｘ＝１５
ｘ＝１２
これを(1)に代入し、ｙ＝９
よって、点Ｆの座標は、Ｆ（１２，９）
ちょっと見にくいので、点の座標をアルファベット順に整理すると、
Ａ（０，１５）、Ｂ（０，０）、Ｃ（２０，０）、Ｄ（２０，１５）、Ｅ（２０，５）、
Ｆ（１２，９）、Ｇ（(２０/３)、５）、Ｈ（(２０/３)、０）
です。題意の斜線部分の面積Ｓとは、ＢＣＥＦで囲まれた面積ですから、
Ｓ＝△ＢＧＨの面積＋□ＣＥＧＨの面積＋△ＥＦＧの面積
です。
△ＢＧＨの高さは、点Ｇと点Ｈのｙ座標から、高さ＝５、底辺は、点Ｂと点Ｈの座標から、
底辺＝(２０/３)
よって、△ＢＨＧの面積＝(１/２)×(２０/３)×５＝(５０/３)
□ＣＥＧＨのｘ軸方向の長さは、点Ｃと点Ｈから、x軸方向の長さ＝(４０/３)、
ｙ軸方向の長さは、点Ｃと点Ｅから、ｙ軸方向の長さ＝５
よって、□ＣＥＧＨの面積＝(４０/３)×５＝(２００/３)
△ＥＦＧの高さは直線ＧＥと点Ｆから、高さ＝４、底辺は、□ＣＥＧＨのｘ軸方向の長さと同じです。
よって、△ＥＦＧの面積＝(１/２)×(４０/３)×４＝(８０/３)
今、求めた三つの図形の面積を全て加えると、
Ｓ＝(５０/３)＋(２００/３)＋(８０/３)＝(３３０/３)＝１１０
答え：１１０平方センチメートル
（２）の解答
正方形ＡＢＣＤを∠Ａを中心に１回転させたと考えると、
正方形ＡＢＣＤの面積×４の正方形と、∠Ａを中心とし正方形ＡＢＣＤの対角線の長さを半径と
する外接円ができあがります。
（正方形ＡＢＣＤ×４からはみ出した面積）＝（半径ＡＣの外接円）−（正方形ＡＢＣＤの面積×４）
ですね。
正方形ＡＢＣＤの一辺の長さは、正方形ＡＢＣＤの面積が５０より、
（一辺）＝√５０＝５√２
（対角線の比）：（正方形の一辺の比）＝１：√２
ですから、対角線…つまり半径ｒの長さは、
ｒ＝５×√２×√２＝１０
（正方形ＡＢＣＤ×４からはみ出した面積）＝（半径ＡＣの外接円）−（正方形ＡＢＣＤの面積×４）＝１０×１０×π−５０×４＝１００π−２００
ですね。
正方形ＡＢＣＤを∠Ａを中心に９０°回転させたとしたら斜線部分の面積Ｓは
Ｓ＝（正方形ＡＢＣＤの面積）＋（正方形ＡＢＣＤ×４からはみ出した面積）／４＝５０＋２５π−５０＝２５π
つまり、∠Ａ＝０°のときＳ＝０。∠Ａ＝９０°のときＳ＝２５πだから、９０°の（１／３）、つまり３０°だけ回転したとき
Ｓ＝２５π／３
答え：（２５π／３）平方センチメートル
（ペンネ−ム：teki）
１ １１０ｃｍ2 ２ 25/3*πｃｍ2
＜解法＞
１は、思い切り数学を使い、原点をＡとする座標を使って解きました。
つまり、２つの対角線（？）の交点の座標は、２直線の方程式から
（１２，９）となるので、後は直角三角形２つと長方形１つに分割して
面積を求めました。
２は、思い切り算数で解きました。
斜線部の面積は、面積移動をすると、正方形の対角線を半径とする
中心角３０度の扇形の面積と等しくなります。
正方形の対角線の長さは、与えられた正方形の２倍の面積を持つ
正方形を考えると、ちょうどこの辺の長さに等しいので１０ｃｍと解り
ます。
あとは、面積を計算するだけですね。
自分でも、天邪鬼な解き方だと思います。はい。
（ペンネ−ム：やなせ）
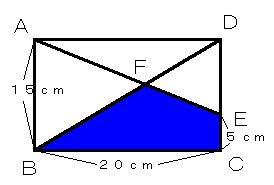
問い１について
四角形ＡＢＣＤは長方形なので辺ＤＣに出来る交点をＥ、線ＡＥとＢＤの交点をＦとすると、
三角形ＡＢＦとＤＥＦそれぞれの角度は角ＡＦＢ＝角ＤＦＥ、角ＦＡＢ＝角ＦＥＤ、
角ＡＢＦ＝角ＥＤＦになりこのことから二つの三角形は相似形の三角形になる事がわかります。
（説明は、はっしょちゃいます。平行線とそれに交わる直線との角度・・・）
相対する１辺の長さがそれぞれ１５ｃｍと１０ｃｍで高さの合計が２０ｃｍですから
三角形ＤＥＦの高さは２０÷（１５＋１０）×１０＝８ｃｍになります。
四角形ＥＦＢＣは三角形ＤＢＣから三角形ＤＥＦの面積を
引いたものになりますから
三角形ＤＢＣの面積は２０×１５÷２＝１５０平方センチメートル
三角形ＤＥＦの面積は１０×８÷２＝４０平方センチメートル
よって四角形ＦＢＣＥの面積は１５０−４０＝１１０平方センチメートルに
なります。
問い１の答えは１１０平方センチメートルです。
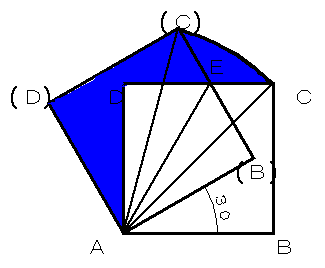
問い２答え
元図の□A,B,C,Dの辺DCと３０度回転させた□A,(B),(C),(D)の辺(C)(B)の交点をEとした時、
問題の図形面積は以下の式で表されます。
図形A,(D),(C),C,Dの面積=多角形A,(D),(C),E,Dの面積＋扇形E,(C),Cの面積・・式１
次に多角形A,(D),(C),E,Dの面積ですが
多角形A,(D),(C),E,Dの面積＝□A,(B),(C),(D)の面積−◇A,(B),E,Dの面積
となりこれを式２とします。
又◇A,(B),E,Dの面積は辺A(B)と辺ADの長さはそれぞれ正方形の一辺だから、
辺A(B)＝辺ADとなり、同じ様な理由で∠ADE＝∠A(B)Eとなりそこから
辺DEと辺E(B)の長さは辺DE＝辺E(B)となり又、辺AEは共通なので△A,D,Eと△A,(B),Eの面積は
２辺とその間の角度が等しいので△A,D,E=△A,(B),Eになります。・・これを”条件１”とし、
このことから
◇A,(B),E,Dの面積は◇A,(B),E,Dの面積＝△A,D,Eの面積×２
となりこれを式３とします。
式３を式２に代入すると以下のようになります
多角形A,(D),(C),E,Dの面積＝□A,(B),(C),(D)の面積−△A,D,Eの面積×２
となりこれを式４とします。
次に扇形E,(C),Cの面積ですが以下の様に表すことが出来ます。
扇形E,(C),Cの面積＝扇形A,(C),Cの面積−△A,(C),Eの面積−△A,E,Cの面積・・式５
ここで△A,(C),Eの面積と△A,E,Cの面積ですが辺AE共通で辺ACと辺A(C)は
同型の正方形の対角線ですのこれ又等しく、その間の角度∠(C)AEと∠EACは
条件１から∠DAE＝∠EA(B)さらに
∠(C)AE＝∠DAE−∠DA(C)＝∠DAE−(45-30)
∠EAC＝∠EA(B)−∠(B)AC＝∠EA(B)−(45-30)
∴∠(C)AE＝∠EAC
よって２辺とその間の∠が等しい場合は二つの三角形は同じである事から
△A,(C),E＝△A,E,Cになります。これを式５に代入すると
扇形E,(C),Cの面積＝扇形A,(C),Cの面積−△A,E,Cの面積×２
となりこれを式６とします。
又△A,E,Cの面積は
△A,E,Cの面積＝△D,C,Aの面積−△A,D,Eの面積
になりますからこれを式６に代入すると
扇形E,(C),Cの面積＝扇形A,(C),Cの面積−△D,C,Aの面積×２＋△A,D,Eの面積×２
になります、これを式７とし△D,C,Aの面積は□A,(B),(C),(D)の面積の半分でこれを
２倍する訳ですから△D,C,Aの面積×２＝□A,(B),(C),(D)の面積
となりますこれを式７に代入すると
扇形E,(C),Cの面積＝扇形A,(C),Cの面積−□A,(B),(C),(D)＋△A,D,Eの面積×２
となりこれを式８とします。
式１に式４と式８をそれぞれ代入すると
図形A,(D),(C),C,Dの面積＝□A,(B),(C),(D)の面積−△A,D,Eの面積×２＋
扇形A,(C),Cの面積−□A,(B),(C),(D)の面積＋△A,D,Eの面積×２
＝扇形A,(C),Cの面積
となりこれを式９とします。
さて扇形A,(C),C の面積ですが正方形A,B,C,Dの面積が５０ｃｍ２で∠CABは４５度から半径ACの長さは
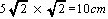
∠(C)AC＝∠DAB−∠(B)AB−∠CA(B)−∠DA(C)
＝90−30−(45−30)−(45−30)＝30なので
扇形A,(C),Cの面積は
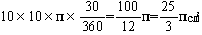となり式９から、求められている図形A,(D),(C),C,Dの面積は
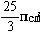です。
（ペンネ−ム：ドラ）
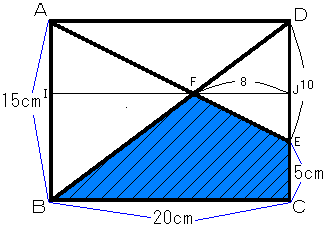（１）の答えは１１０ｃｍ2
まず、CからDの方向へ５ｃｍ（以降、単位ｃｍ省略）の点を点E、
AEとBDの交点を点Fとする。
さらに、点Fを通り、ADに平行な直線とAB,CDとの交点を、
それぞれ I，Jとする。
△ABFと△EDFについて、
AB//DEより、
∠BAF＝∠DEF（錯覚） ・・・@
∠ABF＝∠EDF（錯覚） ・・・A
@，Aより、２組の角がそれぞれ等しいので、
△ABF∽△EDF ・・・B
AB＝１５， DE＝DC−EC＝１５−５＝１０
より、AB：DE＝３：２。
だから、ＦＩ：ＦＪ＝３：２になることと、ＦＩ＋ＦＪ＝２０より、
ＦＪ＝２０×２/５＝８。
よって、△ＥＤＦ＝１０×８×１/２＝４０
ここで、△ＢＣＤ＝２０×１５×１/２＝１５０ なので、
求める面積は、
△ＢＣＤ−△ＥＤＦ＝１５０−４０＝１１０（ｃｍ2）
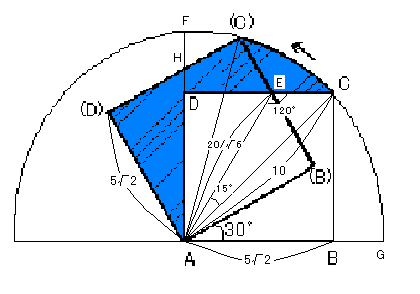
（２）の答えは２５π/３ｃｍ2
（回転に関しては、点Ａを中心に左回りを正とする）
まず、辺ＣＤと辺（Ｂ）（Ｃ）の交点をＥとする。
次に、図のように半円の補助線も引いておく。
正方形ＡＢＣＤの面積が５０ｃｍ2だから、
正方形の一辺は５√２。
△ＡＢＣについて、
∠Ｂ＝９０°，∠ＢＡＣ＝∠ＢＣＡ＝４５°より、ＡＣ＝１０。
∠ＣＡ（Ｂ）＝∠ＣＡＢー∠（Ｂ）ＡＢ＝４５°ー３０°＝１５°
同様に（ＡＥに関して対称に考えて）、∠ＤＡ（Ｃ）＝１５°
∠ＤＡＣ＝９０°や、以上の事より、∠ＣＡ（Ｃ）＝３０°
正方形ＡＢＣＤと正方形（Ａ）（Ｂ）（Ｃ）（Ｄ）は、
ＡＣ（またはＡ（Ｃ））がＡＥに重なっている状態から、
点Ａを中心にそれぞれ１５°，−１５°回転したもの
と考えられるので、 ・・・(1)
∠ＣＡＥ＝∠（Ｃ）ＡＥ＝１５°
△ＡＣＥについて、
∠ＡＣＥ＝４５°，∠ＣＡＥ＝４５°なので、
∠ＡＥＣ＝１２０°
正弦定理より、
１０/ｓｉｎ１２０°＝ＡＥ/ｓｉｎ４５°
これを解いて、ＡＥ＝２０/√６
ここで、加法定理より、
| ｓｉｎ１５° | ＝ｓｉｎ（６０°ー４５°） |
| ＝ｓｉｎ６０°ｃｏｓ４５°ーｃｏｓ６０°ｓｉｎ４５° | |
| ＝・・・（省略）・・・＝（√６−√２）/４ |
| △ＡＥＣ | ＝（１/２）×１０×（２０/√６）×ｓｉｎ１５° |
| ＝・・・（省略）・・・ | |
| ＝２５（３−√３）/３ |
| （２５π／３）ー２×２５（３−√３）/３ | |
| ＝ | （２５π／３）ー５０（３−√３）/３ |
| （１/２）{（２５π/３）ー５０（３−√３）/３} | |
| ＝ | （２５π/６）ー２５（３−√３）/３ ・・・(2) |
| {（２５πー５０）／２}ー{（２５π／６）ー２５（３−√３）／３} | |
| ＝ | ・・・（省略）・・・ |
| ＝ | （２５π／３）−（２５√３／３） ・・・(3) |
| △Ａ（Ｄ）Ｈ＝５√２×（５√６/３）×１/２ | |
| ＝ | ・・・（省略）・・・ |
| ＝ | ２５√３/３ ・・・(4) |
（ペンネ−ム：スモークマン）
1)110
交点でできる三角形は相似だから、小さいほうは、10ｘ8/2=40で、
結局、15ｘ20/2-40=110 とわかります。
2)25π/3
正方形の方の斜線部は、50から、正三角形を引けばよいから
、50-2√50/√3ｘ√50/2=50-50√3
扇型の面積は√2√50が半径で、30/360を掛けて、πｘ25/3
これから、15°、120°、45°の三角形を2固分引けばよいが、
これは、底辺が、√50-√50/√3で、高さが√50だから、50-50/
√3 つまり、πｘ25/3 が残ります。
√を使わずに、小学生はどうするんでしょうね？
（ペンネ−ム：勝浦捨てる造）
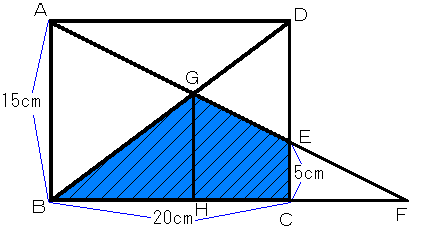
（１）Ａから右下に伸びている直線がＤＢと交わる点をＧ、
ＤＣと交わる点をＥ、ＢＣの延長線と交わる点をＦ、とすると
僊BF と僞CFとは相似だから
１５：（２０＋Ｘ）＝５：Ｘから
Ｘは１０で AＢ：ＢＦ＝EＣ：ＣＦ＝１：２
次にＧからＢＣ上に垂線を下ろしてＢＣ上の点をＨとすると凾fＨＦも僊ＢＦとは相似になるから
ＡＢ：ＢＦ＝ＧＨ：ＨＦ＝１：２
そこで今かりにＧＨをＰcm とすればＨＦは ２Ｐcmですね。
次に凾fＨＢは凾cＣＢと相似だと分るから
ＤＣ：ＣＢ＝ＧＨ：ＨＢで
１５対２０は １対４/３だから ＧＨ：ＨＢ＝Ｐ：(4/3)Pとなって
これより ＨＢ：ＨＦ＝（４/３）Ｐ：２Ｐ＝２：３になるので、ＢＦ＝３０を
２対３で分割すると １２：１８だから ＨＢは１２ｃｍ
ＨＦは１８cmで ＨＣも８cmと判明し それにＧＨも9ｃｍ と分る。
従って求める面積は 凾fＨＢの面積に四角形[台形/]ＧＨＣＥの面積を加えたものだから
三角形ＧＨＢの面積は 12×9×１/２＝５４
台形ＧＨＣＥの面積は14×８×１/2＝５６ から
５４＋５６＝１１０ 答え１１０ｃｍ2
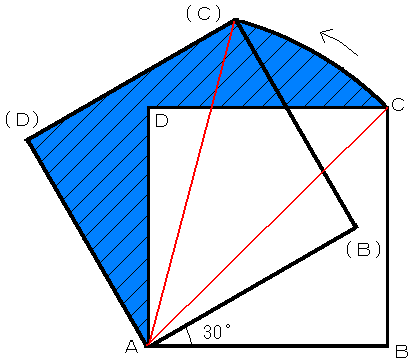
（２）（Ｃ）とＡ、ＣとＡを結ぶ２本の補助線を引くだけでほぼ終わり。
つまり求める面積は 扇形Ａ（Ｃ）Ｃに凾`（Ｄ）（Ｃ）を加えたものから
凾`ＤＣを引いたものが求める面積
ところが凾`（Ｄ）（Ｃ）は凾`ＤＣが ３０度回転したものだから、
扇形Ａ（Ｃ）Ｃの面積が斜線部分の面積と等しいことがわかる．
ところで ∠（Ｃ）ＡＣは ４５ー（４５−３０）＝３０で ３０度
ＡＣの長さは （√５０）2＋（√５０）2＝（Ｘ）2からＸ＝１０で１０センチ
従って求める扇形の面積は １０×１０×π×３０/３６０＝ （２５/３）π 答え （２５/３）π
（ペンネ−ム：ＡＫ）
１．△BDCの面積は、１５×２０÷２＝１５０p2
そのうち上部のいらない部分は相似の関係から、底辺＝１０、高さ＝８で、面積は４０．
引いて１１０p2。
２．A-（C）とA-Cを結ぶ。
弧AC(C)は半径１０の円の１２分の１の面積の扇なので
１００π×１２分の１．
残ったA(C)(D)とACDの面積は足すと正方形ABCDの面積と同値になるから５０．
図形全体の面積から正方形ABCDの面積を引くと、
１００π×１２分の１＋５０−５０＝１００π×１２分の１
が斜線の面積。計算して
２５π／３ p2。
もし円周率πを「３」と考えるなら面積は２５p2。
（ペンネ−ム：けんたん）
（１）の解答
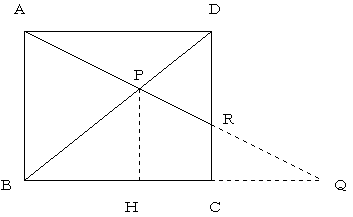
題意より、
ＣＤ上のＣから５ｃｍの点をＲ、ＡＲとＢＤの交点をＰ、ＡＲとＢＣの交点をＱ
ＰからＢＣ上に下ろした垂線との交点をＨとおきます。
△ＱＲＣ∽△ＱＡＢより
ＣＲ：ＢＡ＝ＱＣ：ＱＢ＝ＱＣ：（ＢＣ＋ＣＱ）
ＣＲ＝５ｃｍ ＢＣ＝２０ｃｍ ＡＢ＝１５ｃｍより
１５×ＱＣ＝５×（２０＋ＱＣ）
∴ＱＣ＝１０ｃｍ
△ＡＰＤ∽△ＱＰＢより
ＡＤ：ＢＱ＝２０：（２０＋１０）＝２：３
∴ＰＨ＝ＡＢ×３/（２＋３）＝９ｃｍ
よって、
□ＰＢＣＲ＝△ＰＢＱ−△ＲＣＱ
＝３０×９/２−１０×５/２
＝１１０
答え １１０cm2
（２）の解答
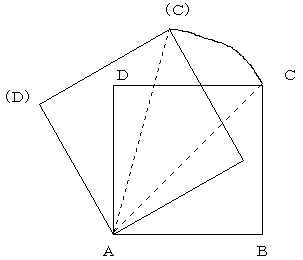
求める面積をＳ（cm2）とすると、
Ｓ＝△Ａ（Ｃ）（Ｄ）＋扇形ＡＣ（Ｃ）−△ＡＤＣ
＝扇形ＡＣ（Ｃ）
＝ＡＣ×Ａ（Ｃ）×３．１４×３０／３６０
ここで
□ＡＢＣＤ＝５０
＝ＡＢ×ＢＣ
＝ＡＣ×ＢＤ／２
＝ＡＣ×Ａ（Ｃ）／２ なので
ＡＣ×Ａ（Ｃ）＝１００
よって、
Ｓ＝１００×３．１４×３０／３６０
＝１５７/６
答え １５７/６cm2
（ペンネ−ム：yokodon）
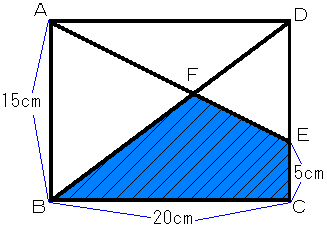
【第１問】
辺ＣＤを 1 : 2 に内分する点をＥ（よって ＣＥ＝ 5 ）、線分ＡＥと線分ＢＤの
交点をＦとします。
三角形ＡＢＦと三角形ＥＤＦは相似であり、相似比はＡＢ:ＥＤ＝ 3 : 2 なので、
高さの比もこれに等しくなります。
これから、三角形ＥＤＦの高さは 20×2/5 ＝ 8 。
求める部分の面積は、従って、
| （求める面積） | ＝（三角形ＢＣＤの面積）-（三角形ＥＤＦの面積） |
| ＝ 15×20/2 - 10×8/2 | |
| ＝ 110（cm2） ・・・（答） |
【第２問】
図中の点（Ｃ）、点（Ｄ）をＣ'、Ｄ' と記すことにします。
線分ＡＣをひいてみると、求める部分の面積の計算方法は一目瞭然でしょう。
三角形ＡＣＤと三角形ＡＣ'Ｄ' は合同なので、
| （求める面積） | ＝（三角形ＡＣＤの面積）＋（扇形ＡＣＣ' の面積）−（三角形ＡＣ'Ｄ' の面積） |
| ＝（扇形ＡＣＣ' の面積） | |
| ＝ π×ＡＣ2 ×30/360 |
（ペンネ−ム：モルモット大臣）
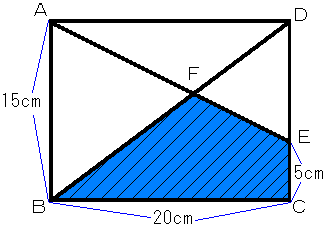
(1) 四角形ABCDにおいて線分CD上で点Cより5cmの点をEとし、線分AEと線分BDの交点
をFとします。このとき求める斜線部の四角形BFECは三角形BCD-三角形EFDここで三角
形ABFと三角形EFDは相似であり、相似比は15:(15-5=10)=3:2であるこから三角形EFD
の線分DEを底辺とした高さは20×2/(2+3)=8
以上から斜線部の四角形BFECの面積は20×15/2-10×8/2=110
答 110cm2
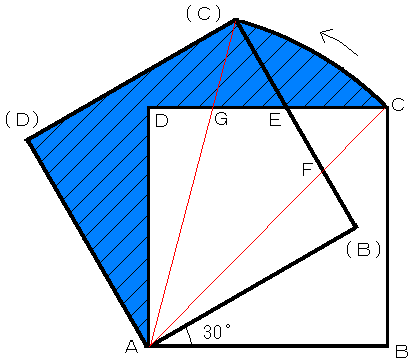
(2) 線分(B)(C)と線分CDの交点をE、線分ACと線分(B)(C)の交点をF、線分CDと線分A
(C)の交点をGとおきます。ここで5角形ADG(C)(D)と三角形ACGの面積に注目すると、
5角形ADG(C)(D)=三角形A(D)(C)-三角形ADG=50/2-三角形ADG
三角形ACG= 三角形ACD-三角形ADG= 50/2-三角形ADG
よって 5角形ADG(C)(D)と三角形ACGの面積は等しい。以上から求める斜線部の面積は
正方形ABCDの対角線を半径とする中心角30°の扇形AC(C)の面積に等しい。扇形AC(C
)=AC2×π×30/360 (AC×AC/2=50よりAC2=100から)
扇形AC(C)=100π/12=25π/3
答 25π/3 cm2
（ペンネ−ム：BossF）
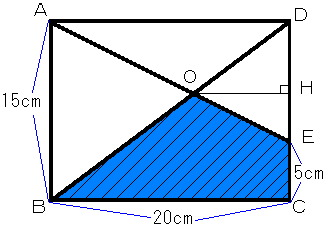
(1)CからDにむかって5cmの点をE、
AEとCDの交点をO、
さらにOからCDに下ろした垂線の足をHとします。
DE=10ｃｍより、OH=20x2/(2+3)=8cm
したがって、△ODE=10x8÷2=40
だから S=150-40=110cm2…答
(2)切り貼りすると、結局、扇形AC(C)になりますから、
正方形の対角線の長さをAとすると
AxAxπx30/360
ところが、正方形の面積はAxA÷2ですからAxA=100
したがって、S=25π/3 cm2 …答
（ペンネ−ム：kirkland）
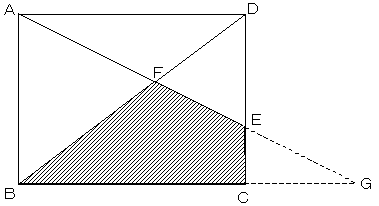
１．ありきたりなやり方しか思い浮かびませんが。
△ＡＢＦ∽△ＤＥＦを使って、後は適当にやる。
もしくは、△ＥＤＡ∽△ＥＣＧと△ＡＦＤ∽△ＧＦＢを使って、後は頑張る。
いずれにせよ、110cm２
２．小学生が普通にやるのなら、「全体−白い部分」と考えて、
△ＡＢＣ＋△Ａ(Ｃ)(Ｄ)＋扇形ＡＣ(Ｃ)−正方形ＡＢＣＤ＝扇形ＡＣ(Ｃ)＝25π/３ (cm２)
今風(？)に円周率を３で計算すると25cm２ とやるのでしょうが、
以下のような変形によって、中心角30°の
扇形に変形できます。面倒なので証明は省略しますが。
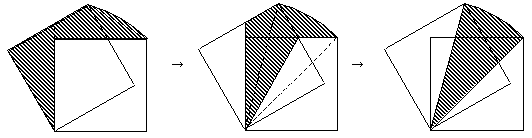
このような変形は、何度回転させたときでも可能です。
下図は、20°回転させたときの変形です。３回やれば、中心角20°の扇形になります。
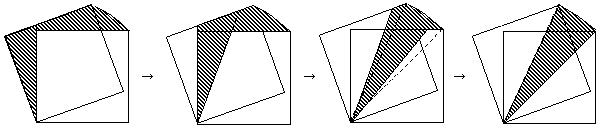
回転させる角度をθとして、【ａ】という記号がａより小さくない最小の整数を表すことにすると
（例：【3.1】＝４、【２】＝２ 変形ガウス？）、
【45/θ】回の変形で扇形になります。
（ペンネ−ム：夜ふかしのつらいおじさん）
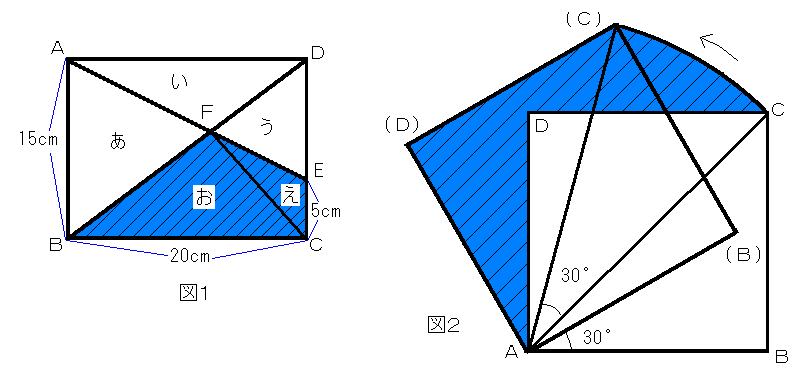
１ 求める面積は １１０ 平方センチメートルです。
図１のように補助線を引きそれぞれの三角形の面積を あ 〜 お とします。
あ：い＝３：２ ［△FBA∽△FDEなのでFB:FD=AB:ED=3:2 より］
い：う＝３：２ ［△FBA∽△FDEなのでAF:EF=AB:ED=3:2 より］
う：え＝２：１ ［DE:EC=2:1より］
あ＝お ［それぞれ底辺BF、AB・sin(∠ABF)=CD・sin(∠CDF)より］
すると、 あ：い：う：え：お＝９：６：４：２：９ となります。
| だから求める面積（え＋お） | ＝四角形ABCD×（え＋お）／（あ＋い＋う＋え＋お） |
| ＝３００×１１／３０ | |
| ＝１１０ |
２ 求める面積は ２５π／３ 平方センチメートルです。
図２のように補助線を引きます。
求める面積は、扇形AC(C) と △(C)(D)A とを合わせたものから△CDAを引いたものです。
ところが △(C)(D)A＝△CDA ですから、結局 扇形AC(C) を求めればよいことが分かります。
正方形ABCDの面積が５０平方センチメートルですから
対角線ACは ２×面積の平方根の１０センチメートルです。
| だから求める面積（扇形AC(C)） | ＝半径×半径×π×３０度／３６０度 |
| ＝１０×１０×π×１／１２ | |
| ＝２５π／３ |
（ペンネ−ム：高橋 道広）
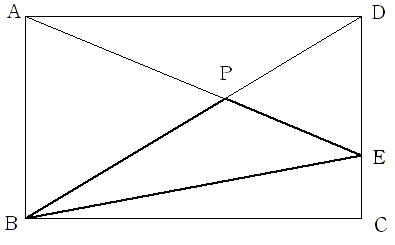
(1)三角形ABPと三角形EDPは相似で 相似比はAP:EP=AB:ED=15:10=3:2
三角形BEP=2/5×三角形ABE=2/5×1/2×15×20=60
三角形BCE=1/2×20×5=50
よって110cm2
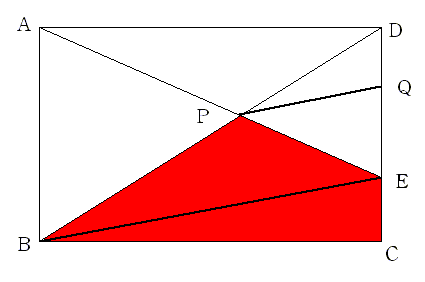
(1)別解
まず三角形ABPと三角形EDPは相似で相似比は
BP:DP=AB:ED=15:10=3:2
BEと平行にACとBDの交点Pを通る直線を引きCDとの交点を
Qとする。
DQ:QE=DP:PB=2:3 QE=10×3/5=6cm
求める面積は
三角形BCE+三角形BFP=三角形BCE+三角形BFQ=三角形BCQ
=1/2×20×(5+6)=110cm2
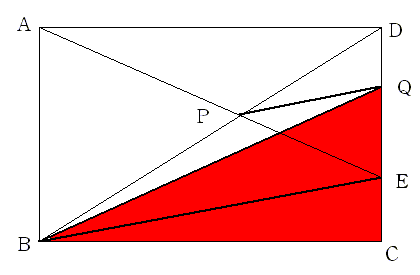
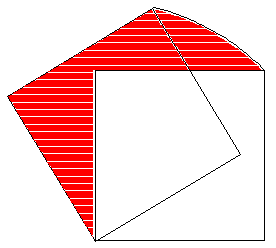
zu2.gif
(2)もとの図形zu2.gifに直角二等辺三角形を足してzu3.gif
同じ面積の直角二等辺三角形を除くとzu4.gif 扇形になる。
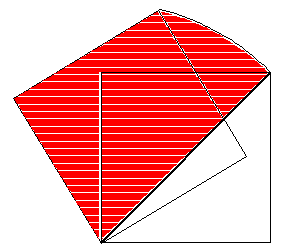
zu3.gif
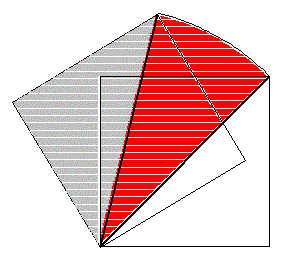
zu4.gif
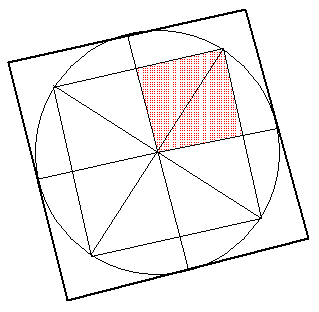
zu5.gif
弧C(C)を作る円の半径を一辺とする正方形の面積はzu5.gif
zu6.gifから100cm2で
あることがわかるので、円の半径は10cmとなる。
よって斜線の部分の面積は 102π×30/360=25/3πとなります。
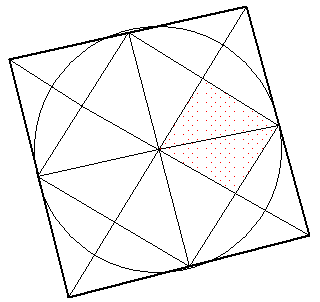
zu6.gif
| モルモット大臣 | けんたん | 勝浦捨てる造 | ||||||
| teki | ドラ | 高橋 道広 | ||||||
| やなせ | yokodon | 岡田
| 夜ふかしのつらいおじさん
| スモークマン
| ＡＫ
| meira
| kirkland
| BossF
| |
今回の問題も中学入試の問題ということで、小学生の知識でどう解くのだろうかと考えてくださった 方が多かったようです。
１番については、三角形の相似、相似比を利用するのがよさそうですね。 夜ふかしのつらいおじさんの解答は、 長方形の中で分割される三角形の面積比を求めるというユニークな解答です。 また、高橋 道広さんの別解は、 「三角形の面積は底辺と高さで決まる」という性質を上手に利用した鮮やかな解答だと思います。
２番については、皆さん苦労されているようですが、扇形の面積に帰着できればあとはすんなりです。
扇形の面積の出し方は、πｒ2×(中心角/360)なので、ｒ(＝ＡＣ)の大きさを知りたいわけです。 しかし、BossFさんや、 モルモット大臣さんの解答にあるように、 ｒの値を知らなくても、ｒ2がわかればそれでいいわけです。 つまり根号を知らなくてもこの問題を解くことはできるわけです。
戻る
top
E-mail