95.77の倍数
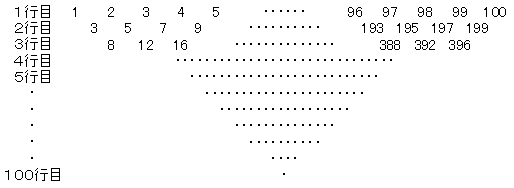
下の表は、1行目には1から100までの整数を1つずつ、すべて書き並べ、 2行目以降はある決まりに従って最後の100行目まで並べたものです。 この表の中に77で割り切れる数は全部でいくつありますか?
Weekend Mathematics/問題/問題95
95.77の倍数
下の表は、1行目には1から100までの整数を1つずつ、すべて書き並べ、 2行目以降はある決まりに従って最後の100行目まで並べたものです。 この表の中に77で割り切れる数は全部でいくつありますか?

算数オリンピックに挑戦
'00〜'03年度版
算数オリンピック委員会編
2001年第10回算数オリンピックファイナル問題
解答・その1
(ペンネ−ム:kiyo)
62個。
NO. 1個 1行目 77 NO. 2個 2行目 77 NO. 3個 3行目 308 NO. 4個 4行目 308 NO. 5個 5行目 1232 NO. 6個 6行目 1232 NO. 7個 7行目 4928 NO. 8個 8行目 4928 NO. 9個 9行目 19712 NO. 10個 10行目 19712 NO. 11個 11行目 78848 NO. 12個 12行目 78848 NO. 13個 13行目 315392 NO. 14個 14行目 315392 NO. 15個 15行目 1261568 NO. 16個 16行目 1261568 NO. 17個 17行目 5046272 NO. 18個 18行目 5046272 NO. 19個 19行目 20185088 NO. 20個 20行目 20185088 NO. 21個 21行目 80740352 NO. 22個 22行目 80740352 NO. 23個 23行目 322961408 NO. 24個 24行目 322961408 NO. 25個 25行目 1291845632 NO. 26個 26行目 1291845632 NO. 27個 27行目 5167382528 NO. 28個 28行目 5167382528 NO. 29個 29行目 20669530112 NO. 30個 30行目 20669530112 NO. 31個 31行目 82678120448 NO. 32個 32行目 82678120448 NO. 33個 33行目 330712481792 NO. 34個 34行目 330712481792 NO. 35個 35行目 1322849927168 NO. 36個 36行目 1322849927168 NO. 37個 37行目 5291399708672 NO. 38個 38行目 5291399708672 NO. 39個 39行目 21165598834688 NO. 40個 40行目 21165598834688 NO. 41個 41行目 84662395338752 NO. 42個 42行目 84662395338752 NO. 43個 43行目 338649581355008 NO. 44個 44行目 338649581355008 NO. 45個 45行目 1354598325420032 NO. 46個 46行目 1354598325420032 NO. 47個 47行目 5418393301680128 NO. 48個 48行目 5418393301680128 NO. 49個 50行目 21673573206720512 NO. 50個 52行目 86694292826882048 NO. 51個 54行目 346777171307528192 NO. 52個 56行目 1387108685230112768 NO. 53個 58行目 5548434740920451072 NO. 54個 60行目 22193738963681804288 NO. 55個 62行目 88774955854727217152 NO. 56個 64行目 355099823418908868608 NO. 57個 66行目 1420399293675635474432 NO. 58個 68行目 5681597174702541897728 NO. 59個 70行目 22726388698810167590912 NO. 60個 72行目 90905554795240670363648 NO. 61個 74行目 363622219180962681454592 NO. 62個 76行目 1454488876723850725818368
解答・その2
(ペンネ−ム: 浜田 明巳)
最近愛用のノートパソコンがダウンしてしまいましたので,昔のDOSマシンを引っぱり出して解きました.昔懐かしいN88BASICです.シラミつぶしで計算し,答が62個になります.
100 'SAVE "WM0411.BAS",A
110 DIM A(100,100)
120 KOTAE=0
130 FOR GYOU=1 TO 100
140 FOR RETSU=1 TO 100-(GYOU-1)
150 IF GYOU=1 THEN A(RETSU,1)=RETSU ELSE A(RETSU,GYOU)=A(RETSU,GYOU-1)+A(RETSU+1,GYOU-1)
160 A(RETSU,GYOU)=A(RETSU,GYOU) MOD 77
170 PRINT A(RETSU,GYOU);
180 KOTAE=KOTAE-(A(RETSU,GYOU)=0)
190 NEXT RETSU
200 PRINT
210 'PRINT GYOU;"行目までに77の倍数は";KOTAE;"個あります."
220 NEXT GYOU
230 PRINT "答は";KOTAE;"個です."
240 OPEN "WM0411.DAT" FOR OUTPUT AS #1
250 WRITE #1,KOTAE
260 CLOSE #1
270 END
解答・その3
(ペンネ−ム:三角定規)
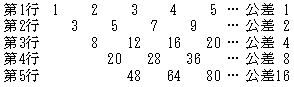
上図のように,各行の数字列の作られ方から わかるように,第m行は 公差 2m-1 の等差数列 である。各行の初項は,
第3行が 8=1・1+2・2+1・3
第4行が 20=1・1+3・2+3・3+1・4
第5行が 48=1・1+4・2+6・3+4・4+1・5
であることから,第m行の初項は
よって,第m行は,初項 (m+1)2m-2 公差 2m-1 の等差数列で,その第n項 f (m,n) は
(1) m=1のとき,f (1,n)=n で,f (1,77)=77 が77の倍数。
(2) m≧2のとき,f (m,n) が77の倍数 ⇔ m+2n−1 が77の倍数。
(※)より, m+2n−1 =77 or 154
1°m=2k+1 のとき,2k+2n=154 ∴ k+n=77
(※)より,2k+1+n≦101 ∴ 2k+n≦100 ∴ 1≦k≦23
よって,このとき 77の倍数となる f (m,n) の個数は 23個。
2°m=2k のとき, 2k+2n−1=77 ∴ k+n=39 ∴ 1≦k≦38
よって,このとき 77の倍数となる f (m,n) の個数は 38個。
以上より,77の倍数となる f (m,n) の個数は 1+23+38=62個 …[答]
この規則から作られる 77の倍数 f (m,n) で最大のものは,
f (76,1)=77・274=1,454,488,876,723,850,725,818,368
f (m,n) の中で最大のものは,
f (100,1)=101・298=32,008,177,655,762,792,387,791,755,935,744
解答・その4
(ペンネ−ム:巷の夢)
ある数字に着目し、その数の下に続く数字をみると必ずある数の倍数となっていることが分かります。例えば、3、12、48となります。このことから77がある行を探せば良いことが分かります。77があるのはまず、1行目の後ろから24番目です。又、2行目の38番目にも77が存在します。更に検討すると以上の2ケースしかないことが判明します。
ところで1行目後ろから24番目の77に続く数の合計は24個です。同様に2行目の38番目の77に続く数の合計は38個です。これらより求めるものは62個となります。
解答・その5
(ペンネ−ム:杖のおじさん)
数列 77のある項数 初項 最終項 項数 1行目の n 77番目 1 100 100 2行目の 2n+1 38番目 3 199 99
1行目は項数が100、数列nなので最終項が100なので77で割れる数は1個です
2行目は項数が99、数列2n+1なので最終項が199なので77の倍数である 77と154があるか調べます。
2n+1=77を解きn=38 2n+1=154を解きn=76.5
従って2行目には77で割れる数字は1つあります。
下に続くある数字は1行目の数列n及び2行目の数列2n+1の4倍の数字の数列であることがわかります。ある数字の倍数である事はその倍数で割ることが出来ます。 従ってその倍数が幾つあるか調べれば答えが出ます。
ある数字が、その数列の項数の半分より左にある時は
(その数字の項数)が個数です。
ある数字が、その数列の項数の半分より右にある時は
(その数列の項数)−(その数字の項数)+1が個数です。
1行目 100−77+1=24
2行目 38
答えは24個+38個=62個あります
解答・その6
(ペンネ−ム:Mr.X)
2n-1行目の数列を{a(n,k)}(1以上k,102-2n以下)
2b行目の数列を{b(n,k)}(1以上k,101-2n以下)
a(n+1,k)=4a(n,k+1) かつ b(n+1,k)=4b(n,k+1)
従って、{a(n,k)}(1以上n,(100-76)以下)の各行に1個ずつ
{b(n,k)}(1以上n,(77-1)/2以下)の各行に1個ずつ
合計62個77の倍数が存在します。
解答・その7
(ペンネ−ム:小学名探偵)
答え:62
解答:
1行 76 77 78 76+77 77+78 3行 77*4上の図からわかるように、奇数行において、77の倍数の位置は変わりません。 そして、2行下るごとに、数(カードとみてよいです)の並びから端の2枚が消えま す。
1行目において、77の位置は左端より右端に近く、100(右端)までに24 (=100-77+1)枚のカードがあります。 この24が奇数行に含まれる77の倍数の個数です。
38 39 2行 77同様に、偶数行において、77の倍数の位置は変わりません。 2行目において、77は左端に近く、左端から38番目のカードです。 この38が偶数行に含まれる77の倍数の個数です。 したがって、24+38=62 が答えとなります。
解答・その8
(ペンネ−ム:高橋 道広)
答 62個
解説
1行目 1,2,3,4,...,n,n+1,n+2、n+3,98,99,100となっているときに
2行目 3 5 7 2n+1,2n+3 2n+5...197,199
3行目 8 12 4n+4 4n+8... 396
となっているので 3行目は1行目を4倍して 両端の数を除いたものになっている。
3行目の数列は4でわっても77の倍数であることに影響がないから
3行目を改めて2,3,4,...99とおいて考えてもよいことになる
すると4行目には2行目の両端の数を除いた数列となり
5行目には2行目の両端の数を除いた数列となっている。
1行目に77の倍数は77のみがある
2行目に77の倍数は n+(n+1)が奇数であることから
n+(n+1)=77から n=38 38番目にあり
77×3=231であるから これだけしかないことがわかる。
奇数行だけ取り出した数列を考えると
1: 1,2,3,4,, ...100
2: 2,3,4,5,...,99 (実際はその4倍)
3: 3,4,5,6,7...98 (実際はその16倍)
...
50: 50,51 (実際はその249倍)
この数列で最後に77がある列は
○,○...77 となるときであるから
101-77=24列目であり 以上から 偶数列には24回出現することがわかる
偶数列をとりだすと
1: 3,5,7,9,...,199
2: 5,7,9,...,197
3: 7,9,11,...,195
...
49: 101
先に書いたように77はこの数列の38項目であるからこの数列には38回出現する
以上から 24+38=62回となります
解答・その9
(ペンネ−ム:Toru)
解答1 奇数行目と偶数行目を分けて考える。
作り方から、3行目は1行目の3つの並んだ数のまん中の数の4倍を並べたものにな り、5行目は3行目の3つの並んだ数のまん中の数の4倍を並べたものになる。4倍 しても、77の倍数かどうかに影響を与えないから無視すれば結局、1行目から順に 両端を除いて並べればよい
1,2,3,4,-------------------------------------------------------,100 2,3,4,----------------------------------------------------,99 3,4,------------------------------------------------,98
このうち77の倍数は77のみでこれは100―76=24行目までにふくまれる。
偶数行目も同様に4倍を無視すれば
3,5,7,9,--------------------------------------------------,199 5,7,9,----------------------------------------------,197 7,9,------------------------------------------,195
ここでも77の倍数は77のみで77=38×2+1よりこれは38行目までに含ま れる。
よって求める答は 24+38=62
ということなのですが、実は最初は下のように腕力で解きました。とてもエレガント ではありませんが、せっかくなので、一応書いておきます。
解答2
n行目、左からk番目の数字をA(n,k) (n=1,2,3,----,100 、 k=1,2,----,(101-n))と すると、題意よりA(1,k)=kでn≧2の時
A(n,k) = A(n-1,k)+A(n-1,k+1) = A(n-2,k)+2A(n-2,k+1)+A(n-2,k+2) = A(n-3,k)+3A(n-3,k+1)+3A(n-3,k+2)+A(n-3,k+3) = ----------- = A(1,k)+ n-1C1A(1,k+1)+ n-1C2A(1,k+2)+-----+ n-1Cn-1A(1,k+n-1) = k+(k+1) n-1C1+(k+2) n-1C2+-------+(k+n-1) n-1Cn-1
ここで、
(x+1)n-1= 1+n-1C1x+n-1C2x2+---- +n-1Cn-1 xn-1
の両辺にxkをかけて微分すると
kxk-1・(x+1)n-1+xk・(n-1)(x+1)n-2=kxn-1+(k+1)n-1C1xk+(k+2) n-1C2xk+1+---+(k+n-1)n-1Cn-1xk+n-2
ここでx=1とすると
A(n,k)=k+(k+1)n-1C1+(k+2)n-1C2+------+(k+n-1)n-1Cn-1 =k2n-1+(n-1)2n-2=2n-2・(2k+n-1) (n=1でも成立)
よって2k+n-1が77の倍数の条件を考えることになるが、
2k+n-1≦201-n≦200より 2k+n-1=77 ----1) と2k+n-1=154 ----2)の場合を考えればよい。
1) 2k =78-n よりn偶数でn=2,4,-----,76のすべてが条件を満たし、38個
2) 2k=155-n よりn奇数、n+k≦101とからn≦47 n=1,3,----,47の24個
よって合計62個
解答・その10
(ペンネ−ム:蜘蛛の巣城)
1段目 1 2 3 4 5・・・・・・・・・・・・・・・・・・・・・・・・98 99 100 2段目 3 5 7 9 ・・・・・・・・・・・・・・・・・・・・・・・・・ 197 199 3段目 8 12 16 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ 396 4段目 ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ ・ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ ・ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・ ・ ・ ・・・・・・・・・・・・・・・・・・ ・ ・・・・・・・・・・・・・・ 98段目 * * * 99段目 * * 100段目 *
この規則で各段が生起するなら、98段目までは等差数列だと言って構わないと思います、証明は省きますが。それで、任意の隣接3段において最上段の任意の隣接3数から生起する数を以下のように整列させましょう。
A−d A A+d 2A−d 2A+d 4A
「数A」と1段とばした真下の(不正確な表現ですが)「数4A」とは、「77」の倍数であるか否かが一致します。
さて、第1段の「77」の倍数は「77」のみ。奇数段の「77」の真下に位置する数はすべて「77」の倍数で、それ以外にはありません。「77」は右から24番目に位置します。奇数段を1段降るごとに右から(謂はば対角線的に)1つずつ項が減りますから、奇数段を24段数えて「77」の倍数は終わりです。その下は項がありません。
また、第2段でも「77」の倍数は「77」のみ。「77」は左から38番目に位置します。(一般項 2n+1(n=1,2,3・・・・・・99)ですね。)奇数段での考察と同様に、偶数段を38段数えて終わりです。
段数の合計62段が、即ち「77」の倍数の個数62個に等しいことになります。
解答・その11
(ペンネ−ム:夜ふかしのつらいおじさん)
答は62個です。
2行目以降の「ある決まり」とは、「隣りあう2数の和をその2数の間に書く」です。
1 2 3 4 5 ・・・ 3 5 7 9 ・・・ ・・・・・・・・・
(1)この問題を考えるとき、元の数を77で割った余りを見ていけば十分です。
余りが39をこえるときは77を引いて負の数で表した方が考えやすいと思いま す。(39を−38、40を−37と表します)
例えば、
99+100 = (77×1+22)+(77×1+23) = 77×2+45
ですが、99、100をそれぞれ77で割った余りの22と23だけ見ればよい のです。
1行目には77で割り切れる数は、77の1つだけです。
そこで77の近辺を見てみます。・・・ 75 76 77 78 79 ・・・ ・・・・・・ 151 153 155 157 ・・・ ・・・・・・・・・ 304 308 312 ・・・ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・
これを
・・・ −2 −1 0 1 2 ・・・・・・ ・・・・・・ −3 −1 1 3 ・・・・・・・ ・・・ −8 −4 0 4 8 ・・・・ ・・・・・ −12 −4 4 12 ・・・・・ ・・ −32 −16 0 16 32 ・・・ ・・・・・・・・・・・・・・・・・・・・・・・・・
と表します。 すると、奇数行目に「0」が現れ、77で割り切れる数があることが分かりま す。
2行下がると右側の数が1つ少なくなります。
100−77=23より、2×23+1=47行目の77の真下の数が最後の7 7で割り切れる数です。(24個あります)
次に38+39=77なので、38と39の近辺を見てみます。
・・・ 36 37 38 39 40 41・・・ ・・・・・ 73 75 77 79 81・・・ ・・・・・・・ 148 152 156 160・・・ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
これを
・・・ 36 37 38 −38 −37 −36・・・・ ・・・・・・ −4 −2 0 2 4・・・・・ ・・・・・・・・ −6 −2 2 6・・・・・・ ・・・・・ −16 −8 0 8 16・・・ ・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・・
と表します。 すると、偶数行目に「0」が現れ、77で割り切れる数があることが分かります。
2行下がると左側の数が1つ少なくなります。
2×38=76行目の38と39の間の真下の数が最後の77で割り切れる数で す。(38個あります)
これで少なくとも24+38=62個あることが分かりました。
(2)次は(1)で調べたもの以外にはないことを考えます。
1 2 3 4 5 6 7 8 ・・・・(公差:1) 3 5 7 9 11 13 15 ・・・・(公差:2) 8 12 16 20 24 28 ・・・・(公差:4) 20 28 36 44 52 ・・・・(公差:8) 48 64 80 96 ・・・・(公差:16) ・・・・・・・・・・・・・・・・
このようにm行目の公差は 2m-1です。
m行目に77で割り切れる数77×kがあったとします。(kは自然数です)
その数を基準として、n番目の数をf(77,n)と表すことにします。
(nは整数で、その数自身は0番目と考えます)
f(77,n)=77×k+2m-1×n
一方、77=7×11です。
ですから f(77,n) が77で割り切れるためには、n自身が77で割り切れなければなりません。
これは、f(77,n)の前後で77で割り切れる数は、77個前か後ろであることを意味します。
(1)の結果から、奇数行目は1行目の77の位置に、偶数行目は1行目の38 と39の間に77で割り切れる数があることが分かりました。
m行目は、(101−m)個の数があります。
どの行も77で割り切れる数の前後には77個の数はありません。
どの行も最大で1個しか77で割り切れる数がないので(1)で数えた数しかな いことが分かります。
解答・その12
(ペンネ−ム:kirkland)
A君 「メリークリスマス!」
先生 「おいおい、ちょっと気が早いよ!」
A君 「だって、次に登場するのは1月ですよ。」
先生 「時間がないから、とっととやんなさい。」
A君 「1行目は1,2,3,…,99,100なので77の1個だけです。」
先生 「2行目は奇数の列3,5,7,…,197,199になるので77の1個だけだね。」
A君 「3行目は4の倍数で8,12,16,…,392,396なので308(=77×4)の1個だけです。」
先生 「4行目も4の倍数の列20,28,36,…,780,788になるので308の1個だけだね。」
A君 「5行目は16の倍数で48,64,…,1568なので1232(=77×16)の1個だけです。」
先生 「6行目も16の倍数で…って、いつまでやるつもりだよ!そのまま足していったら数が馬鹿デカくなって大変だぞ。2と77は互いに素なんだから、2で割れるだけ割っていったら?」
A君 「なるほど。こんな感じですね。 1行目 1 2 3 4 5 ……………96 97 98 99 100 2行目 3 5 7 9 11…………… 193 195 197 199 3行目 2 3 4 5 ……………96 97 98 99 ←4で割った商 4行目 5 7 9 11…………… 193 195 197 ←4で割った商 5行目 3 4 5 ……………96 97 98 ←16で割った商 6行目 7 9 11…………… 193 195 ←16で割った商 7行目 4 5 ……………96 97 ←64で割った商 ……………これなら数が小さくて分かりやすいですね。」
先生 「奇数番目は連続する整数の列になるし、偶数番目は連続する奇数の列になるわけだ。あとはそれぞれ別々に考えるだけだ。」
A君 「まずは、奇数番目の列なんですが、この調子でいくと 45行目 23 24 25……76 77 78 47行目 24 25……76 77 49行目 25……76こんな感じですかね。」
先生 「えらく簡単に見つけたね。どうやったの?」
A君 「またまた〜。時間がないのに。列のアタマの数は1ずつ増えていくし、ケツの数は1ずつ減っていくんだから、その和は常に101で一定なんですよ。1行目は1+100=101、3行目は2+99=101…でしょ。それで、アタマの数を2倍して1引くと、何行目かを表す数になることを発見したんですよ!例えば、アタマの数が3になるのは3×2−1=5行目とか。」
先生 「アタマとかケツとか言わずに初項、末項とか言いなさい。」
A君 「まあそういうわけで、奇数番目の列では、1行目、3行目、…、47行目の24個の行に77が含まれます。ついでに、偶数番目もやっちゃいますね。偶数番目の列もこの調子でいくと 74行目 75 77 79……123 125 127 76行目 77 79……123 125 78行目 79……123全部、初項と末項の和が202です。 偶数番目の列では、2行目、4行目、…、76行目の38個の行に77が含まれます。 というわけで、全部で24+38=62個で〜す!」
先生 「まぁ、そんな感じでいいんじゃない」
A君 「では、みなさんよいお年を。」
先生 「だから〜、気が早いってば」
正解者
小学名探偵 kiyo Mr.X 三角定規 巷の夢 Toru 杖のおじさん 浜田 明巳 高橋 道広 夜ふかしのつらいおじさん kirkland 蜘蛛の巣城
実は、1段ぬかしで縦に見ていくと、4倍の数が並んでいくことがわかります。 三角定規さんが示してくださった一般項でも確認できます。
f(m+2,n-1)/f(m,n)=2m/2m-2=22=4
4倍を無視して表示するというToruさんや高橋道広さん、A君の解答はすっきりしていますね。夜ふかしのつらいおじさんのように、77の剰余で考えるという手もあります。いずれも大きい数を扱わなくていいというメリットがあります。そして、77の倍数が縦に並んでいるということに気付けば、数えるのは そうむずかしいことではありませんね。

 E-mail
E-mail
 top
top