Weekend Mathematics乛僐儘僉僂儉幒乛NO.121
| NO.1026 | 2001.9.3. | 昹揷丂柧枻 | 摦偔惓嶰妏宍乮俀乯 |

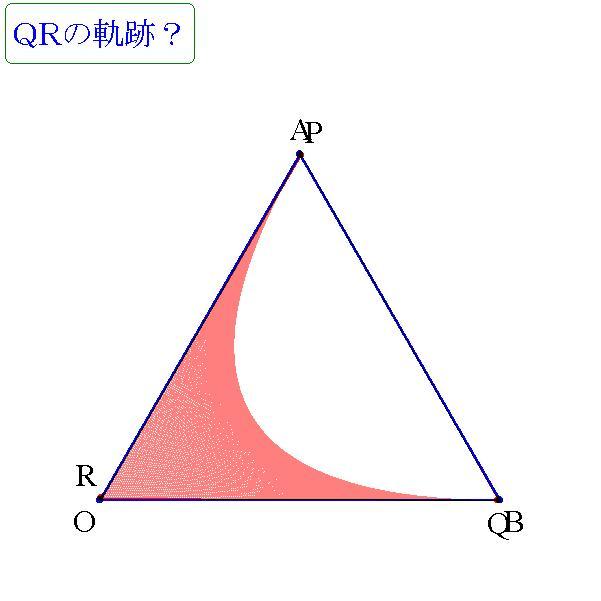
恾偐傜丆媮傔傞椞堟偼丆俷俙丆俷俛傪愙慄偲偡傞曻暔慄偲丆
俷俙偲俷俛偱埻傑傟傞晹暘偱偁傞偙偲偑暘偐傞
乮偳偆偟偰曻暔慄偐丠丂偲偼暦偐側偄偱壓偝偄乯丏
俙俛傪倶幉丆俙俛偺拞揰俵傪尨揰丆俵俷傪倷幉丆俷偼倶幉傛傝壓懁偵丆
俙偼倷幉傛傝塃偵偁傞偲偟偰丆曽掱幃傪偨偰傞丏
俙俛亖俀偱偁傞偐傜丆俙(侾丆侽)偲側傞偺偱丆捈慄俷俙偺曽掱幃偼丆
丂丂倷亖併俁(倶亅侾)
曻暔慄偺曽掱幃傪
丂丂倷亖倎倶2亄倐乮倎亜侽丆倐亙侽乯乧乧乧(1)
偲偡傞偲丆
丂丂倷'亖俀倎倶
愙揰俙(侾丆侽)偵偍偗傞愙慄偺孹偒偼丆倶亖侾傪戙擖偟偰丆
丂丂俀倎亖併俁
丂丂亪倎亖併俁乛俀
(1)偵戙擖偡傞偲丆
丂丂倷亖併俁倶2乛俀亄倐乧乧乧(1)'
俙(侾丆侽)傪捠傞偺偱丆
丂丂侽亖併俁乛俀亄倐
丂丂亪倐亖亅併俁乛俀
(1)'偵戙擖偡傞偲丆
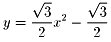
屘偵媮傔傞柺愊偼丆
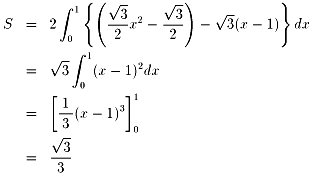

| NO.1027 | 2001.9.4. | Hakuchonn | 柍悢偺慻傒崌傢偣乮俁乯 |
NO.1024偺夝摎偵傕偁傞捠傝弶崁侾丄戞
俀崁偑俀偺僼傿儃僫僢僠悢楍偺婏悢崁俥乮2倠-侾乯丆俥乮2倠亄侾乯偑夝偲側傝傑
偡丅
徹柧偼俥乮値乯俀亖俥乮値-侾乯俥乮値亄侾乯亄乮-侾乯値-侾丂偲偄偆桳柤
側惈幙傪巊偊偽弌棃傑偡丅

| NO.1028 | 2001.9.4. | Hakuchonn | 抦傝崌偄乮俁乯 |
乽俁丆俁丆係恖偺俁僌儖乕僾偵暘偗偨帪偵偳偺僌
儖乕僾偺恖傕丄摨偠僌儖乕僾撪偺恖偲偼抦傝崌偄偱丄偐偮堘偆僌儖乕僾偺恖偲偼抦傝
崌偄偱偼側偄偲峫偊傜傟傞偺偱丄偙偺帪俁亄俁亄俇亖侾俀慻偺抦傝崌偄偑昁梫偱偁
傞丅屘偵侾侾慻偟偐偄側偄偙偲偐傜丄數僲憙尨棟傛傝侾僌儖乕僾撪偵抦傝崌偄偱偼側
偄俀恖偑昁偢懚嵼偡傞偙偲偑暘偐傞丅傛偭偰丄偍屳偄偵抦傝崌偄偱偼側偄係恖偑懚嵼
偡傞丅乮偙傟偼僺乕僞乕愭惗偺夝摎傪巹側傝偵夝庍偟偨傕偺偱偡丅乯乿

| NO.1029 | 2001.9.5. | yokodon | 柍悢偺慻傒崌傢偣乮係乯 |
NO.1027 偺柦戣偺徹柧
F(1)亖1丄F(2)亖2 偐傜 F(3)亖F(1)亄F(2)亖3
偙偺偲偒 (嵍曈)亖 F(2)2 亖 4
丂丂丂丂 (塃曈)亖 F(1)F(3)亄1 亖 4
偲側傝丄n = 2 偱惉棫偡傞丅
偁傞帺慠悢 k 偱偺柦戣偺惉棫傪壖掕偡傞偲丄
F(k)2 亖 F(k+1)F(k-1)亄(-1)(k-1)
偙偺偲偒丄
| F(k+2)F(k) | 亖 {F(k+1)亄F(k)}丒F(k) |
| 亖 F(k+1)F(k) 亄 F(k)2 | |
| 亖 F(k+1)F(k) 亄 F(k+1)F(k-1) 亄 (-1)(k-1) | |
| 亖 F(k+1)丒{F(k)亄F(k-1)} 亄 (-1)(k-1) | |
| 亖 F(k+1)2 亄 (-1)(k-1) |
偱傕丄NO.1024
偺庡挘偼丄摉曽崱偺偲偙傠傑偩悢抣幚尡偱偄偔偮偐妋擣偟偨偩偗偱
偡乮抪偢偐偟側偑傜乯丅(^^;
僼傿儃僫僢僠悢楍偭偰丄偄傠偄傠柺敀偄偙偲偑偁傞傕傫偱偡偹偉丅
傑偩傑偩丄偄傠偄傠梀傋偦偆偱偡偹丅

| NO.1030 | 2001.9.5. | 搉晹丂彑 | 惓曽宍偺愜傝巻乮俁乯 |
乽岺晇椡乿
惗搆偵堦枃丄儁乕僷乕傪梌偊偰偔偩偝偄丅懡偔偺応崌丄偦傟偑丄俛俆斉
偁傞偄偼A4斉僐僺乕梡巻側偳偱偁傞偲偟傑偟傚偆丅
偦傟偱偼丄偙偺梡巻傪巊偭偰惓曽宍傪嶌偭偰壓偝偄丅
弌棃傑偟偨偐丠偙偙傑偱偼彫妛惗偱傕弌棃傞偲巚偄傑偡丅
乮挿偄傎偆偺曈偵抁偄傎偆偺曈偺挿偝傪庢傝丄偦偺揰偱愜傟偽傛偄乯
師偵丄偙偺惓曽宍偺柺愊傪侾偲偟偰丄偦偺柺愊偺侾/2偲側傞惓曽宍傪
偮偔偭偰偔偩偝偄丅
丂丂
偳偆偟傑偡偐丠
巐嬿傪拞怱揰偵崌傢偣傞條偵愜傞丅乮彫妛惗偱傕弌棃傞偐傕偟傟傑偣傫乯
偦傟偱偼丄偦偺堦曈偲側偭偨挿偝傪峫偊偰尒傑偟傚偆丄併俀/俀乮俀暘偺
併俀乯偲側偭偰偄傞偙偲偑敾傝傑偡丅偦偆偱偡柺愊偑1/2偲側偭偰偄傞傢
偗偱偡偐傜丄偦偺堦曈偺挿偝偼併侾/2=併俀/俀偲側傞傢偗偱偡偹丅
偱偼柺愊傪1/2偵偡傞曽朄偼偙傟偩偗側偺偱偟傚偆偐丠
懡偔偺曽朄偑偁傝傑偡偺偱岺晇偟偰偔偩偝偄丄偳偺條偵尒偮偗傞偺偐丄
僾儘僙僗偵傛偭偰偼丄拞妛惗丄崅峑惗岦偗偺僥乕儅偲側傝傑偡丅
丂
偱偼丄侾/3偲側傞惓曽宍偼偳偆偱偟傚偆丄彮偟擄偟偔側偭偰偒傑偡丅
侾/4偼丠偙傟偼娙扨偵弌棃偦偆偱偡偹丄偁傞曽朄偼彫妛惗偱傕弌棃傞偐傕
抦傟傑偣傫丄慠偟懠偺曽朄偼偳偆偱偟傚偆偐丠
弴師丄侾/5 1/6丒丒偲恑傔偰偔偩偝偄丅
峏偵崅搙側僥乕儅偲偟偰偙偺A4斉巻偺柺愊偺侾/3偲側傞惓曽宍傪偮偔偭偰偔偩偝偄丅
堦枃偺儁乕僷乕傪庤偵幚姶偟側偑傜乽岺晇偡傞椡乿傪崅傔傞帠偵側傝傑偡丅
師偵丄偦傟傜偺曈傪丄恾宍偲偟偰丄偁傞偄偼寁嶼抣偲偟偰媮傔妋擣偟傑偡丅
Help: 僽儖乕僶僢僋僗乽愜傞巻偺悢妛乿

| NO.1031 | 2001.9.5. | 俢俢俿 | 摦偔惓嶰妏宍乮俁乯 |
No.1026偺昹揷偝傫傊偺戝偒側偍悽榖偱偡丅
巹傕丄戣堄偺椞堟偺奜宍慄偼曻暔慄偩偲巚偄傑偡丅
傑偢惓嶰妏宍偺柧傜偐側懳徧惈偐傜丄RQ偼恾-1偺傛偆偵摦偔偲巚偄傑偡丅
恾-1偱偼寁嶼偟偵偔偄偱偡偑丄揔摉側侾師曄姺偱恾-2偺忬懺偵堏傟傞偼偢偱偡丅
偙偙偱O'A'亖O'B'亖1偲偟傑偡丅
0亝兟亝1偱偡丅O'B'丆O'A'曽岦偵x幉偲y幉傪棫偰傟偽丄捈慄R'Q'偼丄
y亖亅(1亅兟)/兟亄(1亅兟)
偲側傝丄兟亖0傕峫椂偡傟偽丄
(1亅兟)x亄y兟亖兟(1亅兟) (1)
偱偡丅幃(1)傪兟偵偮偄偰惍棟偡傞偲丄
兟2亄(亅x亄y亅1)兟亄x亖0 (2)
偱丄捈慄R'Q'偺憒偔椞堟偱偡偐傜丄(2)偑0亝兟亝1偲側傞擟堄偺夝兟傪帩偰偽椙偄偼偢偱偡丅
偦偺昁梫廫暘忦審偼丄(2)偺嵍曈傪f(兟)偲偟偨偲偒丄
嘆丗 f(0)亖x 亞0 乮戣堄傪枮偨偡乯
嘇丗 f(1)亖y 亞0 乮戣堄傪枮偨偡乯
嘊丗
| 俢 | 亖(亅x亄y亅1)2亅4x |
| 亖x2亄y2亄1亅2xy亅2y亄2x亅4x | |
| 亖x2亅2xy亄y2亅2x亅2y亄1 | |
| 亖(x亅y)2亅2(x亄y)亄1 | |
| 亞0 |

| NO.1032 | 2001.9.6. | Junko | 惓曽宍偺愜傝巻乮係乯 |
柺愊1/3偺惓曽宍偺愜傝曽偵偮偄偰丄峫偊偰傒傑偟偨丅
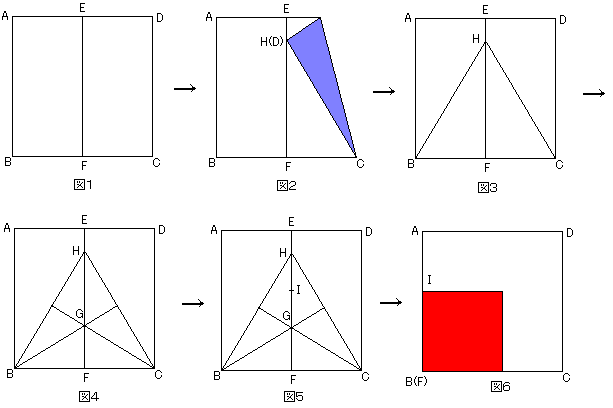
傑偢敿暘偵愜偭偰丄愜傝栚俤俥傪摼傑偡丅乮恾侾乯
捀揰俢偑俤俥偵廳側傞傛偆偵偍傝傑偡乮俫乯丅乮恾俀乯
峏偵俫俠丄俫俛偵愜傝栚傪偮偗傑偡丅偙傟偱惓嶰妏宍俫俛俠偑偱偒傑偟偨丅
惓曽宍偺侾曈偺挿偝傪侾偲偡傞偲丄俫俥亖併俁/俀偲側傝傑偡丅乮恾俁乯
嶰妏宍俫俛俠偺拞慄傪愜傞偙偲偱丄偦偺岎揰俧傪摼傑偡丅
偙傟偼嶰妏宍俫俛俠偺廳怱偵側傝傑偡丅
廬偭偰丄俫俧丗俧俥亖俀丗侾乮恾係乯
峏偵丄俫俧傪愜傞偙偲偱偦偺拞揰俬傪摼傑偡丅
俫俬亖俬俧亖俧俥亖(併俁/俀)丒(侾/俁)亖併俁/俇
俬俥亖併俁/俁乮恾俆乯
俬偱丄俙俢偲俛俠偑暯峴偵側傞傛偆偵愜傞偙偲偱丄俬俥偺挿偝傪俙俛忋偵偲傝傑偡丅
偙傟(挿偝併俁/俁)傪侾曈偲偡傞惓曽宍傪嶌傟偽丄偦偺柺愊偑偪傚偆偳侾乛俁偱偡丅
柺愊1/5偺惓曽宍偺愜傝曽偵偮偄偰偼丄栤戣俆侽丂柺愊俆暘偺侾偺栤戣
偑嶲峫偵側傞偲巚偄傑偡丅

| NO.1033 | 2001.9.7. | 昹揷丂柧枻 | 寽徿儅僯傾偺擸傒 |
偆偪偼壠懓慡堳寽徿儅僯傾偱偡丏
傕偆偠偒僐仜僐乕仜惢昳偺寽徿偺掲傔愗傝偑嬤偯偄偰偄傑偡偺偱丆
柍棟偺側偄斖埻偱墳曞僔乕儖傪廤傔偰偄傑偡丏
偙偙偱丆師偺媈栤偑晜偐傫偱偒傑偟偨丏
侾枃偺怽崬梡巻乮梩彂乯偱丆侾岥偐傜俁岥傑偱偺怽偟崬傒偑弌棃傞偺偱偡丏
侾枃偱侾岥偩偗側傜丆偦偺梡巻傪柍嶌堊偵慖傇偩偗偱丆岞暯側拪慖偑弌棃傞偲巚偄傑偡丏
偟偐偟丆俀岥傗俁岥偺梡巻偐傜慖傇偵偼偳偆偡傟偽偄偄偺偱偟傚偆偐丏
傑偝偐俀岥丆俁岥偺梡巻偐傜丆侾岥偺梡巻偲摨條偵慖傇偺偼丆晄岞暯偱偁傝丆嵓媆偱偡丏
幚嵺偵偳偺傛偆偵拪慖偝傟偰偄傞偺偐丆偛懚偠偺曽偑偄傜偟偨傜丆惀旕偍嫵偊壓偝偄丏
偍婅偄偟傑偡丏旕忢偵婥偵側傞栤戣側偺偱偡丏
巹側傝偵峫偊偰傒偨寢壥丆師偺傛偆偵偡傟偽岞暯側偺偱偼側偄偐丆偲巚偄傑偡丏
傑偢侾岥丆俀岥丆俁岥偺梡巻偺枃悢傪偦傟偧傟悢偊傑偡丏
妋棪寁嶼偵傛偭偰丆侾岥梡偺摉慖幰悢丆俀岥梡偺摉慖幰悢丆俁岥梡偺摉慖幰悢傪偦傟偧傟寛掕偟丆
偦偺悢偺暘偩偗拪弌偡傞偺偱偡丏
椺偊偽丆師偺傛偆偵側傝傑偡丏侾岥暘偑侾侽侽侽恖偺墳曞悢丆
俀岥暘偑俀侽侽侽恖偺墳曞悢丆俁岥暘偑俁侽侽侽恖偺墳曞悢偩偭偨偲偟傑偡丏偡傞偲慡晹偱丆
丂丂侾亊侾侽侽侽亄俀亊俀侽侽侽亄俁亊俁侽侽侽亖侾係侽侽侽
岥偺墳曞偑偁偭偨偙偲偵側傝傑偡丏
摉慖幰悢偑俀俆侽柤偩偲偡傞偲丆侾岥暘偺墳曞幰偺拞偐傜丆
丂丂侾亊侾侽侽侽亊俀俆侽乛侾係侽侽侽亖侾俈.俉乧乧乧佮侾俉
俀岥暘偺墳曞幰偺拞偐傜丆
丂丂俀亊俀侽侽侽亊俀俆侽乛侾係侽侽侽亖俈侾.係乧乧乧佮俈侾
俁岥暘偺墳曞幰偺拞偐傜丆
丂丂俁亊俁侽侽侽亊俀俆侽乛侾係侽侽侽亖侾俇侽.俈乧乧乧佮侾俇侾
暘偺梡巻傪偦傟偧傟拪弌偡傟偽偄偄偙偲偵側傝傑偡丏
巐幪屲擖偺娭學偱岆嵎偑弌傞応崌偼丆偦偺暘傪揔摉偵妱傝怳傝傑偡丏
杮摉偺偲偙傠偼偳偆側傫偱偟傚偆偐丏偙傟偱偄偄傫偱偟傚偆偐丏
偦傟偲傕丆戝偒側惡偱偼尵偊傑偣傫偑丆傕偭偲揔摉偵傗偭偰偄傞傫偱偟傚偆偐丏

| NO.1034 | 2001.9.10. | 搉晹丂彑 | 惓曽宍偺愜傝巻乮俆乯 |
惓曽宍偺捀揰傪嵍忋偐傜A,B,C,D,偲偟傑偡丅
偼偠傔偵曈AD偺拞揰BC偺拞揰傪寢傇愜傝慄傪嶌傝傑偡丅
懕偄偰曈BC傪B傪婲揰偵愜傝丄捀揰C偑愭偵嶌偭偨
愜傝慄偵廳側傞條偵偟傑偡丅
偙偺偲偒偵嶌傜傟偨愜傝慄偲曈CD偲偺岎揰傪E偲偡傞偲
挿偝CE偼侾/併俁偲側傝傑偡丅
傎偐偵傕曽朄偑偁傝傑偡丅
HELP丗僽儖乕僶僢僋僗乽愜傞巻偺悢妛乿

| NO.1035 | 2001.9.11. | Junko | 惓曽宍偺愜傝巻乮俇乯 |
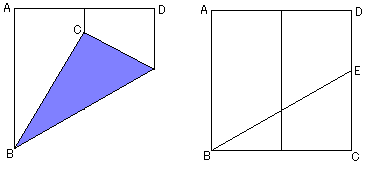
NO.1034搉晹丂彑偝傫偺愜傝曽傪恾偵偟偰傒傑偟偨丅
佢俤俛俠亖俁侽亱偵側傝傑偡偺偱丄妋偐偵偦偆偱偡偹丄偲偭偰傕僔儞僾儖両丂慺惏傜偟偄偱偡丅

 E-mail
E-mail
 栠傞
栠傞