 (1)
(1)になると思います。ここで区間[a,b]はf(x)とg(x)の定義域の共通分。 どうしてか? 以下は完全に個人的意見です。
Weekend Mathematics/コロキウム室/NO.134
| NO.1145 | 2002.2.1. | DDT | ユークリッド距離(3) |
NO.1139 ユークリッド距離(2)の後を継いでるつもりです。
NO.1135 ユークリッド距離(1)のシーラカンスさんの「ある分布から、もうひとつの分布」を
「ある関数f(x)から、もうひとつの関数g(x)」の意味に解釈すれば、
「ある関数f(x)から、もうひとつの関数g(x)までのユークリッド距離」は、
ユークリッド距離(2)の定義より、
 (1)
(1)
になると思います。ここで区間[a,b]はf(x)とg(x)の定義域の共通分。
どうしてか? 以下は完全に個人的意見です。
① 関数をベクトルと考える.
手順はこうです。[a,b]に含まれる全ての独立変数xに、x=xiと番号付けする。
そして、
(f(x1),f(x2),f(x3),f(x4),・・・,f(x∞)) (2)
と並べてベクトルをつくる。上記ベクトルを一目で見渡せる人は(そんな人はいませんが)、
関数f(x)の全ての情報を得ることができる。
なぜなら[a,b]に含まれる任意の独立変数xiに対する
yi=f(xi)の値がわかるから。
よって関数y=f(x)を上記ベクトル形式で表しても良い。
ここで問題になるのは、何故こんなに強引な概念を持ち出す必要があるのか?
答えは便利だから。関数をベクトル形式で扱うことにより、線形代数や解析幾何学や、
普通の統計解析の色々な理論を、関数間の関係に適用できるようになるから。
② ベクトル形式で表された関数間に内積を定義する.
(f(x1),f(x2),f(x3),f(x4),・・・,f(x∞))
(g(x1),g(x2),g(x3),g(x4),・・・,g(x∞))
としたとき、内積(f(x),g(x))は、
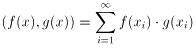 (3)
(3)
とかけるが、これはふつう収束しない。
なぜならf(xi),g(xi)は有限の大きさを持つ量なので、
それらを無限個足せば普通は発散する。正のf(x),g(x)を考えれば、これは明らか。
③ そこで、無限大に大きな単位系に移る.
例えば一部の工学系の世界では、ほんの数年前までCGS(cm,glam,sec)単位系が主流だったが、
現在はSI単位系(m,kg,sec)に移行している。
長さの話に限ればこれは、同じ長さを表す数値であるはずの距離数値1(cm)が、
突然0.01(m)という距離数値に変わったことを意味する。
こんな事を自由しても良い理由は、単位の変更とそれに伴う距離数値の変化は、
実際の物理距離とは無関係だから。いまの場合の物理距離とは、(2)で表されるベクトルが存在できるような、無限次元の直交座標空間。
そのようなものがあるとして、内積(3)が収束するような単位の変更を行う。
(3)はふつう発散するので、選べる単位は無限に大きなものに限られる。
(3)の最初の単位は不明だが、それを1/h倍に大きくした時の(3)の姿だけはわかる。
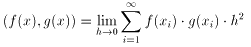 (4)
(4)
(4)のh2をh2=Δxとおきかえれば積分の定義、
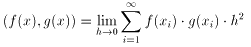 (5)
(5)
と同じなので、
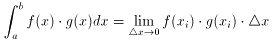 (6)
(6)
と決める。関数の内積を(6)のように決めれば、そこから関数間の距離を計算できるので、(1)となる。

| NO.1146 | 2002.2.1. | 月の光 | 複素数の問題(1) |
どのようにすればよいでしょうか。z5+6z+1=0の根はすべて|z|<5/3を満たし、その内4つは3/2<|z|<5/3 である事を示せ

| NO.1147 | 2002.2.1. | 遊未 | 最速降下問題 (5) |
NO.476 最速降下問題の、図①での最速降下曲線自身を求める式、
どこから離してもゴールにたどりつく時間は同じという主張の証明を、
詳しく知りたいです。
どなたかおねがいします。

| NO.1148 | 2002.2.3. | yokodon | ある不等式の証明(7) |
扇形の面積が「扇形の内部にある二等辺三角形」の面積よりも大きい理由を、微分
を使わずに示すことを考えます。
これを前提にすれば、NO.1122 の“sin(x) < x が x > 0 で成り立つこと”が高
校数学の範囲で保障できそうです。
xy 平面上の単位円 x2 + y2= 1 の第1象限の部分に、 点P ( t , √(1-t2)) と点A ( 1 , 0 ) を取ります。 弧AP上の任意点Xから x 軸に下ろした垂線の足をQ、直線AXと直線XQの交 点をRとし、Xの x 座標を x とおき、f(x) = |XQ| - |XR| とおくことにしま す。
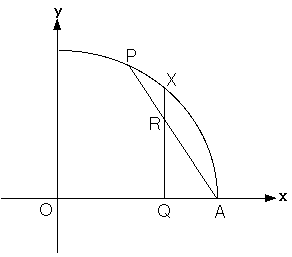
X ( x , √(1-x2) ) 、Q ( x , 0 ) 、P ( x , √(1-t2)/(t-1)・(x - 1) )
ですから、
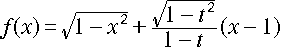
ところで、f(x) を変形すると、t < x < 1 の範囲では以下のように出来ます。
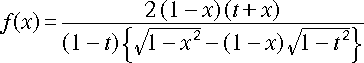
よって、t < x < 1 にて f(x) > 0 です。
また、f(t) = f(1) = 0 です。
従って、t ≦ x ≦ 1 の範囲で、f(x) ≧ 0 が言えます。
(無理関数の微分の公式を認めても、同様の証明が出来るでしょう。が、ここでは省
略します。)
以上のことから、扇形の弧の両端を結ぶ線分は扇形の周又は内部に属し、線分の両
端以外は全て扇形の内部に属することが分かります。従って、扇形の中心角を u(0
< u < π/2)とすると、
(二等辺三角形の面積)= 1/2・sin(u) < 1/2・u =(扇形の面積)
が言えるということになりそうです。

| NO.1149 | 2002.2.3. | yokodon | 関数列の極大点(3) |
NO.1123で、
帰納法による a_n の推測が(万が一)思いつかなかった人のための
?別解です。
とは言え、結局帰納法を使うのですが・・・(^^;
以下の命題を示します。
an < n , n = 1,2,... ・・・[1]
(i) n = 1 のとき
a1= 0 < 1 であるから成立。
(ii) n = m のときの成立を仮定する。
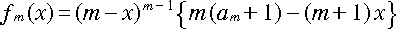
ですが、帰納法の仮定から
m/(m+1)・(am+ 1) - m = m/(m+1)・(am- m) > 0なので、
x = m/(m+1)・(am + 1) のとき、fm(x) は極大となります。
従って、{an} の定義から、
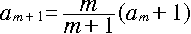
です。このとき、やはり帰納法の仮定から、
| am+1 - (m + 1) | = m/(m+1)・(am+ 1) - (m + 1) |
| = {m(am - m) +(1 - m)}/(m+1) | |
| < 0 |
このことから、{an} の漸化式も、
a1= 0 、an+1= n/(n+1)・(an + 1)
と、求まります。これを解いて、an = 1/2・(n-1) を得ます。

| NO.1150 | 2002.2.3. | yokodon | 最速降下問題 (6) |
この問題を解くのに必要な知識は、以下です。
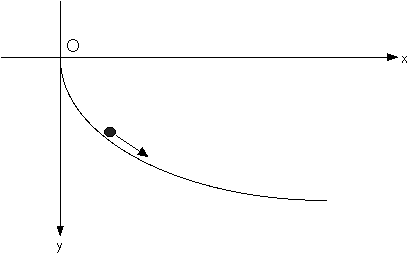
質量 m の物体が、ある曲線 y = f(x) の形状をした滑らかな“斜面”にそって2
次元運動し、摩擦はなく重力のみを外力として受けるものとして考えます。物体の初
速度は、(0,0)とします。
物体の力学的エネルギー保存則は、以上の仮定の下で次式になります。
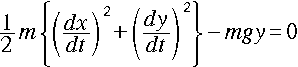 ・・・[1]
・・・[1]
[1] 式を、以下のように書き換えます。2乗の扱いですが、複号の正を取ることに
します。
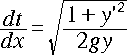 ・・・[2]
・・・[2]
これを、積分します。
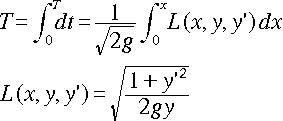
・・・[3]
都合上、右辺の被積分関数を L(x,y,y')と置いています。
さて、この T を最小にするような y = f(x) を求めるわけです。 ここで変分法を使います。「関数 f(x) を“変化”させたときの、T の最小値」を 求めるのが、変分法です。些か数学的な正確さを犠牲にして議論を進めますが、関数 y の任意の“微小変化”を δu とし、このときの T の“変化”をδT とすると、部 分積分から、以下のように変形できます。
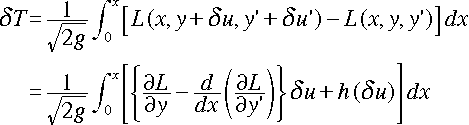 (修正 2/24)
(修正 2/24)
( h(p) は、p の2次以上の整式)
ここで、δu は任意でしたから、δT = 0 となる条件下では、
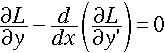 ・・・[4]
・・・[4]
が成り立ちます。これが、『オイラー・ラグランジュ方程式』と
呼ばれるものです。
本問の条件に戻って、[4] を計算すると、整理して最終的に以下のようになります
(途中は、長いので省略しています)。
y'2 + 2yy'' + 1 = 0 ・・・[5]
これを解くと、サイクロイドの曲線の式が出てきます
両辺に y' をかけると、d/dx{yy'2 + y} = 0 となり、x で積分すると、
y' = {(A2-y)/y}1/2 ・・・[6]
という形に出来る(A:積分定数)ので、そこで置換積分をします。
[6] 式で、y = A2・sin2(u/2) とおくと、結局以下の結果を得ます。
x = A2/2・(u - sin(u)) , y = A2/2・(1 - cos(u))
(修正 2/9)
この解の結果から、[3] の値が(x,y の初期値と終点に依存した)定数になること
は、[3] に解を代入して置換積分を実行すると出てきます。

| NO.1151 | 2002.2.3. | yokodon | ラプラス変換(3) |
ここでは、ラプラス変換の応用例として薬物動態論を挙げ(#我田引水)、「数学
が世の中で、如何に役立っているか」という一例をご紹介したいと思います。
まず、薬物動態論がどの様な学問分野であるかを説明します。
この分野は、摂取した薬物の身体の中での動きを、薬物の血中濃度変化から説明す
るための学問分野で、そのやり方の一つに『区画モデル』(注)
というのがあります。
ここで“区画”とは、身体の中で薬物の濃度をひとくくりに出来る部分のことを言
います。身体全体をひとまとめにする場合が「1区画モデル」、身体全体を2つに分
ける場合を「2区画モデル」などといいます。他に、身体の解剖学的あるいは生理学
的な特徴を踏まえたモデルを作る試みも盛んになされ、臨床応用もなされていますが
、簡単のためここでは考えないことにします。
モデルの構成の特徴は“速度論”であって、
[物質量の変化する速度]=[物質の流入速度]-[物質の出ていく速度]
という形をしています。
簡単のため、1区画モデルの場合について考えましょう。
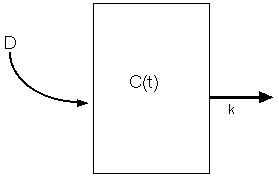
静脈注射で 時刻 t = 0 に薬物を D (mg) だけ入れたものとしましょう。身体の
体積を V (l) とします。
尿中排泄や肝臓での代謝(→化学変化のことです)により、単位時間あたりの薬物
濃度の減少がその時の濃度 C (mg/l) に比例するものとすると、比例定数を k (mg/l
・min) として、濃度の時間変化は、以下のようになります。
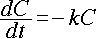 ・・・[1]
・・・[1]
これを、ラプラス変換で解いてみましょう。
関数 X(t) のラプラス変換を L[X(t)]
とし、NO.1141に習って、L[X(t)] が s の関数であるとします。
変換の公式から、L[dC/dt] = C(0) + sL[C] なので、ラプラス変換の線形性も用
いて、[1] 式は以下のように変形できます。
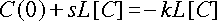
よって、
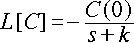
となります。さて、ラプラス変換の線形性と L[exp(-kt)] =
1/(s + k) から、上記の結果に逆変換を施して、
C(t) = C(0)・exp(-kt)
という結果を得ます。
これだけだとちょっと簡単すぎる(かな?と思う)ので、他の場合についても考え
てみましょう。
1区画モデルで、静脈から一定速度 U (mg/l・min) で薬物を注入する(点滴の場
合など)ときの、薬物濃度 C の時間変化は、以下のようになります。
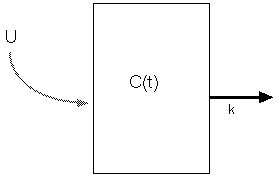
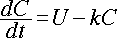 ・・・[2]
・・・[2]
2区画モデルで、区画1の濃度を C1 、区画2の濃度を C2 とし、 区画1→2の 移行過程の速度係数を k12 、2→1の速度係数を k21 、 区画2からのみ薬物が消失するものとしてその速度係数を k0 とすると、 薬物投与を単回投与として各区画 の薬物濃度変化は、以下のようになります (例えば、薬物の作用点の前と後とで、薬物の挙動が異なる場合などが、該当す るでしょう)。
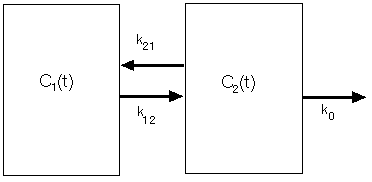
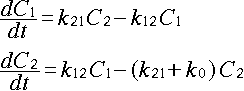
こうした場合を初めとする複雑な場合や、連立方程式になっている場合などに、ラ
プラス変換による「微分演算の代数計算への置き換え」は、威力を発揮します。が、
手続きの本質は、1区画モデルの場合と同じです。
現在、こうした計算はコンピュータを使ってプログラム演算で(実験で測定した速
度係数の値と、薬物の投与量を入力すれば)自動的に行われるようになりました。そ
の成果として、我々は計画的な薬物投与の下で医療を受けることが出来たり、薬物動
態の基礎データに基づいて安全な投与量の薬をもらえるようになってきているわけで
す。「1日2回、食前に飲んで下さい」みたいな薬局での指示などは、こうした理論
と実験のバランスの成果として正当化されているわけです。
注)『区画モデル』という語について;業界では、なぜか片仮名で「コンパートメン
トモデル」と呼ぶ“ことになっている”のですが、長ったらしいし、欧米至上主義的
で敷居が高いので、ここでは簡潔で分かりやすい(と筆者は思っている)この表現を
使うことにします。上記のモデルの考え方からして、片仮名の呼び名に拘る理由が見
いだせないことは、容易にご理解いただけることと思います。

| NO.1152 | 2002.2.9. | 遊未 | 最速降下問題 (7) |
NO.1150 最速降下問題(6)
への質問なんですが、
[1]から[2]への書き換えと、[5]からどうすればサイクロイドの式が出るのか、
そこの部分が考えたんですが、よく分かりません。
できるなら詳しい式を示していただきたいのですが…

| NO.1153 | 2002.2.9. | yokodon | 最速降下問題 (8) |
[1] → [2] の変形と、[5] からサイクロイドの式への変形について、やりかたを
お示ししたいと思います。
(1)[1] → [2] の変形
まず、次の事実に着目します(合成関数の微分)。
dy/dt = dy/dx・dx/dt
これを [1] 式に代入し、整理します。
1/2・m・{1 + (dy/dx)2}・(dx/dt)2 - mgy = 0
これを、dx/dt について、解いてみて下さい。
さて、dt/dx = 1/(dx/dt) ですから、以上から [2] を得ます。
(2)[5] →サイクロイド解
[5] 式の両辺に y' (= dy/dx) を掛けます。
y'3 + 2yy'y'' + y' = 0 ・・・[7]
ところで、
d/dx(y・y'2) = y'3 + 2yy'y''
ですから、微分の線形性から、[7] 式は結局、
d/dx{y・y'2 + y} = 0 ・・・[8]
と同値です。y ≧ 0 に注意して、A2 (A:ある実数)を積分定数として、[8] 式の
積分は
y・y'2 + y = A2
となります。これを y'(= dy/dx)について解いたものが [6] 式です。復号の正を
採りました。
y' = {(A2-y)/y}1/2 ・・・[6]
[6] 式は、変数分離型の微分方程式なので、
∫{y/(A2-y)}1/2 dy=∫dx
と、変形できます。この左辺で、以下の変数変換をします。
y = A2・sin2(u/2)
これで置換積分をすると、最終的な結果になります(No.1150の結果には、積分定
数が A しか出てきていませんが、初期時刻にて(x,y)=(0,0)であることを暗に
使いました)。

 E-mail
E-mail
 戻る
戻る