
Weekend Mathematics�^�R���L�E�����^NO.135
| NO.1154 | 2002.2.10. | ����@�� | ���f���̖��i�Q�j |
���T�{�U���{�P���O
������(cos�Ɓ{��sin��)�Ƃ���Ɓi�����ł����O�̎����j
�@�@(���Tcos�T�Ɓ{�U��cos�Ɓ{�P)�{��(���Tsin�T�Ɓ{�U��sin��)���O
�䂦��
�@�@���Tcos�T�Ɓ{�U��cos�Ɓ{�P���O�A���Tsin�T�Ɓ{�U��sin�Ɓ��O
�����̎�����@cos�T�ƁAsin�T�Ƃ����������
�@�@���P�O�|�R�U���Q�|�P���P�Qcos�Ɓ@�ƂȂ�B
�����ŁA�|�P��cos�Ɓ��P�Ȃ̂ŁA
�@�@�|�P�Q�������P�O�|�R�U���Q�|�P���P�Q��
�ƂȂ�B�]���āA
�@�@���P�O�|�R�U���Q�{�P�Q���|�P���O�@�E�E�E�@
�@�@���P�O�|�R�U���Q�|�P�Q���|�P���O�@�E�E�E�A
��������B
�@��������������ƁA(���T�{�U���|�P)(���T�|�U���{�P)���O
���T�{�U���|�P���O�����T�|�U���{�P���O�@���邢��
���T�{�U���|�P���O�����T�|�U���{�P���O�@�ƂȂ�B
�A��������������ƁA
�@�@(���T�{�U���{�P)(���T�|�U���|�P)���O
���T�{�U���{�P���O�Ȃ̂ŁA���T�|�U���|�P���O
��(��)�����T�|�U���|�P�Ƃ���ƁA��'(��)���T���S�|�U�ƂȂ�A
����(6/5)1/4�ŋɏ��ƂȂ�B
��(5/3)��452/243���O�Ȃ̂ŁA����5/3�D
�B�C�D����1/6�̋ߕӁi���ۂɂ͂O�D�P�U�U�U�S�U�������O�D�P�U�U�U�W�V�j�A3/2������5/3�ƂȂ�B�E
�����ŁA���T�{�U���{�P���O�A�̎������l����B
��(��)�����T�{�U���{�P�Ƃ���ƁA��'(��)���T���S�{�U���O�Ȃ̂ŒP�������̊��ł���B
���������ĂP�̎��������B
��(-1/6)��-1/65���O�A��(�O)���P���O�Ȃ̂ŁA���͈̔͂�-1/6�������O�ƂȂ�B
���̍������A���A���A�Ƃ����|��||��||��||��|���U�Ȃ̂�
�E����ǂ̍��̐�Βl��3/2������5/3�ƂȂ邱�Ƃ��킩��B

| NO.1155 | 2002.2.11. | ���̗��� | �O�p�`�̓��ډ~�i�P�j |
���Y����͍ŋ߁A�^����ꂽ���̋t���l����悤�ɂȂ��Ă��܂��B
�����Ŗ��ł��B
��P�F�R�ӂ̒������R�C�S�C�T�ł���O�p�`�̓��ډ~�̔��a�����߂�B
��Q�F�O�p�`�̓��ډ~�̔��a���P�C���O�ӂ̒����������ł���R�ӂ̒��������߂�B

| NO.1156 | 2002.2.12. | ���̗��� | �������i�R�j |
�����̗��ꁄ����ɓ͂�������ł��B��Q�V��̉��������݂āA
NO.604 �������ɂ��Ă̕��@��
�m���������������B
�u���w�Z�ŁA�������ɂ��Ă���ĂāA����ɂ��Ċe���l������Ė�肪�o����ł��� ������ꉞ�������ł����ǁA�Ō�̖₢���킩��Ȃ��Ē��ׂĂ��Ƃ����i��j�������̑g�ݍ��킹�p�^�[���͂T�Q�ʂ�B ����͕�݂��T�g������ŁA��݂𑝂₵���茸�炵���肷��ƃp�^�[�����ς��B ��݂����g���Ƃ��̃p�^�[�������a���ʂ�Ƃ��悤�B
�i�P�j�a�P�a�Q�a�R�a�S�����߂�B
�i�Q�j�a�U�����߂�B
�i�R�j���͂a�P�a�Q�E�E�E�a���܂ł킩��Ƃ�������a��+1�����߂邱�Ƃ��o����I �ǂ�ȍl�����ɂ��������B
�i�S�j�a�V�`�a�P�O�����߂�B
�i�T�j���̂a�̈Ӗ��͂Ȃɂ�(�R���j
����Ŗl�͂��́i�T�j���킩��Ȃ���ł��B �����킩��Ȃ為�Ћ����Ă��炢������ł����A���肢���܂��B �i�͂����茾���Ă���Ȗ����o���l�͂����������܂���ˁj�v

| NO.1157 | 2002.2.14. | ����@�� | �O�p�`�̓��ډ~�i�Q�j |
�O�p�`�̊e�ӂ̒��������C���C���i�����������j�A���ډ~�̔��a�����Ƃ����
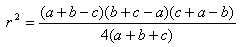
�ƂȂ�B�����ł��{�������C���|�������Ƃ����
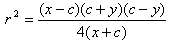
�ƂȂ�A�����P�Ȃ̂�
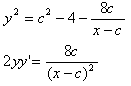
�ƂȂ肙�͂��ɑ��ĒP���������ƂȂ�B���Q���O�Ȃ̂�
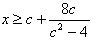
���̍ŏ��l�͂��C���C�����O�p�`�ł��邱�Ƃ��炃�{�P�Ȃ̂�
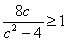
�䂦��
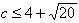
�����W�ƂȂ�
�܂����̍ŏ��l�͔��a�Q�̉~�����ڂ���̂łR�ƂȂ�B
���������ĂR���������������W�̏����ɍi����B
����ɂ��{���{�����Q���Ƃ����
(���|��)(���|��)(���|��)�����ƂȂ�B(���͐���)
����ɂ��{���{�����Q���Ƃ���B
�\���̂��邁�����̑g�ݍ��킹�͈ȉ��̒ʂ肾���A
���̎�������̂́A(���C���C��)��(�R�C�S�C�T)�����ł���B
| �� | �� | �� | �� | (d-a)(d-b)(d-c) |
|---|---|---|---|---|
| �R | �R | �S | �T | �S |
| �R | �S | �T | �U | �U |
| �R | �T | �U | �V | �W |
| �R | �U | �V | �W | �P�O |
| �R | �V | �W | �X | �P�Q |
| �S | �S | �S | �U | �W |
| �S | �S | �U | �V | �X |
| �S | �T | �T | �V | �P�Q |
| �S | �T | �V | �W | �P�Q |
| �S | �U | �U | �W | �P�U |
| �S | �U | �W | �X | �P�T |
| �S | �V | �V | �X | �Q�O |
| �S | �W | �W | �P�O | �Q�S |
| �T | �T | �U | �W | �P�W |
| �T | �T | �W | �X | �P�U |
| �T | �U | �V | �X | �Q�S |
| �T | �V | �W | �P�O | �R�O |
| �U | �U | �U | �X | �Q�V |
| �U | �U | �W | �P�O | �R�Q |
| �U | �V | �V | �P�O | �R�U |
| �U | �W | �W | �P�P | �S�T |
| �V | �V | �W | �P�P | �S�W |
| �W | �W | �W | �P�Q | �U�S |

| NO.1158 | 2002.2.20. | �c�c�s | �ő��~����� �i�X�j |
�ő��~�����̓r������d��𗣂��Ă��A���̉^�������͗������ʒu�ɖ��W�Ȃ��Ƃ������܂��B
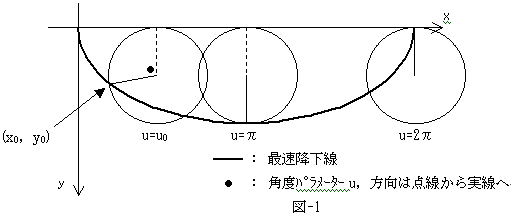
�܂�NO.1150�̌��ʁi2/9�C���Łj���A�^���͏�}�̋Ȑ���ɑ��������1�����^���ł��B
�d��̋O���̑����Ȑ��ł���ő��~�������A���Ұ�u��p���ď����A
�@�@�@x��a(u�|sin u)
�@�@�@y��a(1�|cos u) �@�@�@�@(1)
�ł��B������A2/2��a�Ƃ��܂����Ba�͐}-1�̉~�̔��a�ł��B
�܂��A�ő��~������1�_�ix0(u0)�Cy0(u0)�j���痎������d�肪�A
�����Ȑ���̕ʂ̓_�ix(u)�Cy(u)�j�ɒB����܂ł̌o�ߎ��Ԃ��^���������������ċ��߂���@�́A
u�ɑ���^�������������G�Œ��߂܂����B
�����Ŗ����������Ɍo�ߎ��Ԃ̂��߂���@�����Љ�܂��B
���̕��@�́ANO.1150��[3]�œK�p�Ȓu���ϕ������s����̂Ɠ����ł��B
�ǂ�����G�l���M�[�ۑ�����dt/dx�ɂ��ĉ����āAx�Őϕ����o�ߎ��Ԃ����߂܂��B
�d��̉^����u�Ɋւ���1�����^���Ƃ݂Ȃ���̂ŁA�T�^�I��1�����^�����l���܂��B
�^����\�����W��x�C���xv��dx/dt�Ƃ���ƃG�l���M�[�ۑ����́A
�@�@�@E��T�{U��1/2�mv2�{U(x)�@�@�@�@ (2)
�Ə����܂��B������m�͗��q�̎��ʁCT��T��1/2�mv2�ʼn^���G�l���M�[�C
U��U(x)�͕ۑ��͂��͂̃|�e���V�����ł��B
(2)���^����p�ƍ��Wx�ŏ��������邽�߂ɁA�ˑR�ł������O���W�A���Ȃ���̂��l���܂��B
�@�@�@ L��T�|U��1/2�mv2�|U(x) �@�@�@ (3)
�����O���W�A���ł��BL��L(v�Cx)�ƍl����L��V�ŕΔ�������ƁA�^���ʂ̕\���������܂��B
�@�@�@�݂k/��v��mv�@�@�@�@(4)
�����ʼn^���ʂ�p�Ƃ��Ap��mv��p����(2)����v����������ƁA
�@�@�@E��1/2m�p2�{U(x) �@�@�@�@(5)
�ƂȂ�܂��B�^���ʂƍ��W�ŕ\���ꂽ�G�l���M�[�̕\�����n�~���g�j�A���ƌĂсA
�ӂ�E��H(p�Cx)�ŕ\���܂��B�n�~���g�j�A������́A�^�����������܂��B
�@�@�@��H/��p�� dx/dt�@�@�@�@(6)
�@�@�@��H/��x���|dp/dt�@�@�@(7)
�Ƃ����ƁA�ʏ�̉^��������m�d2x/dt2���|U(x)�������܂��B
�ʏ�̍��W��^���ʂ�p�����ꍇ�A�����̓g���r�A���Ȍ��ʂł����A
��(1)��p�������̂悤�ɔC�ӂɕϊ����ꂽ���W�ɑ��Ă��A
�W(4)�C(6)�C(7)�͂��̂܂܂̌`�Ő��藧�̂ŁA���̏ꍇ�̓g���r�A���ł͂���܂���B
�ȉ��̊W�́A1�����^����\���C�ӂ̍��Wq�ɑ��Đ������܂��B
�^����p�͎�(4)����Ap���݂k/��v�Ƃ��ē�������̂ł��B
��p�ϐ�I��s��ϕ��A
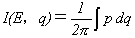 �@�@�@(8)
�@�@�@(8)
�Œ�`���܂��B��p�ϐ�I�̕����I�Ӗ��́A��ʉ��p�^���ʂƂł������ׂ����̂ł����A
�ƂĂ�����������Ȃ��̂ŏȗ����܂��B
I��I(E�Cq)�Ȃ̂́A�G�l���M�[�ۑ����d���g(p�Cq)���Ap��p(E�Cq)�ł��邽�߂ł��B
��I/��E���v�Z���܂��B�ϕ��L�����̔����𗘗p���āA
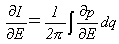 �@�@�@(9)
�@�@�@(9)
�Ə����܂��B�܂��d���g(p(E�Cq)�Cq)���A
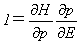
�ƂȂ�A
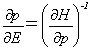
�����藧���܂��B�Ƃ��낪�ip�Cq�j�Ɋւ��鎮(6)�̊W���A
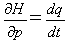
�ł��邽�߂ɁA��p�ϐ�I�̃G�l���M�[E�Ɋւ�������́A
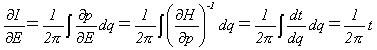 �@�@�@(10)
�@�@�@(10)
�ł��邱�Ƃ��킩��܂��B����Ď�(10)�ɂ��A�^�����J�n����Ă���̌o�ߎ���t���v�Z�ł��܂��B
���̐ϕ��������^���̂P�����Ɋւ��čs���A���炩�^���̎������o�܂��B
��������p�ϐ�I�̒�`(8)������킩��悤�ɁA
I(E�Cq)���v�Z���邽�߂ɂ́Ap��p(E�Cq)�̌`���킩��Ηǂ��̂ŁA
�G�l���M�[�ۑ����̕\���d���g(p�Cq)���K�v�Ȃ����ł��B
�]���Ď��ۂ�q��q(t)�̌`����̓I�ɋ��߂Ȃ��Ă��������v�Z�ł��A
�������C�ӂ̍��W�œ������@���g���܂��B
���̏ꍇ�A���Wu�Ɋւ���͊w�I�G�l���M�[���v�Z���Ă݂�ƁA� �����ԂɊւ�������Ƃ��āA
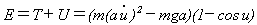 �@�@�@(11)
�@�@�@(11)
�ƂȂ�܂��B��������(11)�ɂ͂܂��A�v�Z�Ɋւ��Ėʓ|���N���������Ȓ��z��(1�|cos u)��
�܂܂�Ă��܂��B�O�p���������珉�����z���ł��낤�ƒ��z���͒��z���ł��B
������x�ϐ��ϊ����āA�K�����ω\�ŁA������x�͑㐔�������\�ȗL�����ւ̋A�������݂܂��B
�@�@�@q=1-cosu�@�@�@(12)
�Ƃ����A
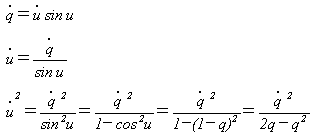
�Ȃ̂ŁA
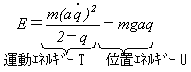 �@�@�@(13)
�@�@�@(13)
�������܂��B���O���W�A��L�́A��(13)�̈ʒu�G�l���M�[�̕�����ς������̂Ȃ̂ŁA
���Wq�ɑ���^����p�́A
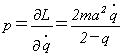 �@�@�@(14)
�@�@�@(14)
�Œ�`����܂��B�������(13)�ɑ������A
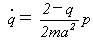
�Ȃ̂ŁA
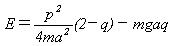 �@�@�@(15)
�@�@�@(15)
�ƂȂ�܂��B�ړI��(p�Cq)�Ɋւ����p�ϐ�I�́A
�G�l���M�[E�Ɋւ��������I/��E���v�Z���邱�Ƃł����A
�ʑ����{(p�Cq)}�ʼn^����\���ƁA���v�Z�ɕ֗��Ȋw�I�Ӗ�����p�ϐ�I��
�^�����܂��B���̂��߂Ɏ�(15)��q�ɂ��ĉ����܂��B
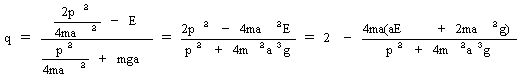 �@�@�@(16)
�@�@�@(16)
�ƕό`�ł���̂ŁA�^���̋O�Ղ͐}-2�ƂȂ�܂��B
�����ŃG�l���M�[E�͐}-1�Ǝ�(11)����A
�@�@�@E(u0)=-mga(1-cosu0)�@�@�@(17)
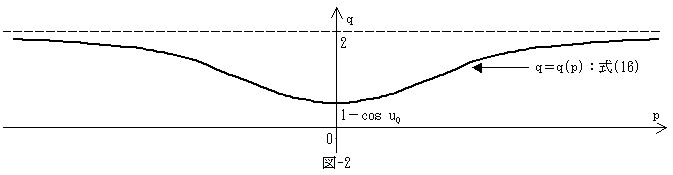
�ł��B�܂���p�ϐ�I�̒�`��(8)�̐ϕ���p�dq�́A
�}-2��q��2�Ǝ�(16)�̋Ȑ��̊Ԃɋ��܂ꂽ�ʐςł��B
�ʐςȂ̂ŁAq��2�Ǝ�(16)��q��q(p)���g���Ē���p�Őϕ����Ă������ł��B
�ϕ��͈͂́A�}-1����u0��u��2�|u0�Ȃ̂ŁAp�Cq�̒�`��(12)�C(14)�����ǂ邱�Ƃɂ��A
u�Ɋւ���^����1�����A
�@�@�@u��u0 �� �� �� 2�|u0 �� �� �� u0
�ɑ��āA
�@�@�@cos u��cos u0 �� -1 �� cos u0 �� -1 �� cos u0
�@�@�@q��1�|cos u
��1�|cos u0 �� 2 �� 1�|cos u0 �� 2 �� 1�|cos u0
�ŁAq�̑����Ɛ}-2�̋Ȑ��̊T�`�i�Q�ߐ���q��2�j�A�����p��2ma2/(2�|q)�dq/dt����A
�@�@�@p��0 �� �{�� �� �|�� �� 0 �� �{�� �� �|�� �� 0
�ƂȂ�܂��B���Ȃ킿�}-2��q��2��q��q(p)���������łȂ������Ȑ��ƍl���āA
��ԓ_(p�Cq)�́Au�Ɋւ���^����1�����̊ԂɁA�Ȑ���2�����܂��B
�]����u��1�����ɑΉ������p�ϐ��́A��(16)������Ȃ̂��l�����āA
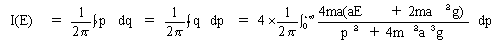 �@�@�@(18)
�@�@�@(18)
�Ə����܂��B�Ƃ���ł��ܗ~�����̂́A��(18)�̐ϕ��l�ł͂Ȃ��A
����E�Ɋւ�������ł��B�s��ϕ��ɂ���`(9)�ɏ]���A
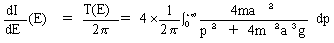 �@�@�@(19)
�@�@�@(19)
�������܂��B�����Ŏ�(19)��T(E)�́A�^���̎���T���A
�d��̎����Ă���͊w�I�G�l���M�[E�̊��ł��邩������Ȃ��ƌ����Ă܂��B
�͊w�I�G�l���M�[E�͎�(17)���A�d��̏����ʒuu0�̊��ł��B
����������Ή^���̎���T��E�ɉe�������Ƃ������Ƃ́A
�d��̏����ʒuu0�ɉe������邱�ƂɂȂ�܂��B
��(19)�̍ʼnE�ӂ̐ϕ���E���܂܂Ȃ��̂ŁA�^���̎���T�̓G�l���M�[E�ɉe������܂���B
�]���čő��~�����U��q�̓������������܂����B���ꂪ�ŏ��̖ړI�ł��B
�ŏ��ɏq�ׂ��悤�ɂ��̕��@�́A
NO.1150��[3]�̐ϕ������s����̂Ɩ{���I�ɓ����ł����A
�͊w���Ƃ���������������邽�߂ɍ�p�ϐ�������ƁA
�������u���̂������قڎ����I�Ɏ����Ă����̂��Ǝv���܂��B

| NO.1159 | 2002.2.20. | Akira | �ő��~�����i10�j |
�ő��~�����ɂ��āB�ǂ̈ʒu���痎�������Ă��������Ԃʼn��ɒH�蒅���A
�Ƃ������Ƃ̏ؖ��̕��@�ƁA�ؖ����̎����ׂ������肽����ł��c�B
��w�̎��Ƃł�������ǁA�Ԃ̌v�Z�⎮�A�ׂ����ؖ����@�������ł��Ȃ��č����Ă܂��B

| NO.1160 | 2002.2.24. | yokodon | �ő��~�����i11�j |
���B���ԂɊւ���
�T�C�N���C�h������A���v���Ԃ����߂镔�������������܂��B
�������Ɋւ���ڂ��������́ADDT ���������ɒ��J�ɂ��ĉ������Ă���̂ŁA�ȗ�
�v���܂��B
NO.1150�� [3] ���ɁA�ȉ��������܂��B
x �� A2/2�E(u - sin(u)) , y �� A2/2�E(1 - cos(u))
�Ƃ���ŁA
dx/du �� A2/2�E(1 - cos(u)) , dy/du �� A2/2�Esin(u)
�ł�����A
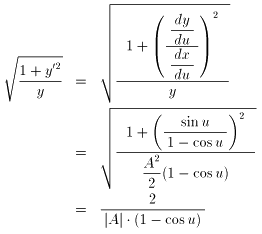
�ƂȂ�܂��i�r���́A�ȗ����܂����j�B
����āA[3] ������At �� T �̂Ƃ��@u ��u1 �ł���Ƃ���ƁA
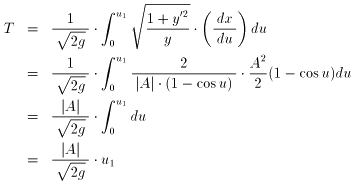
�̂悤�ɂȂ�܂��B
���āAA �� u1 �́A���ɋȐ��̊T�`�����߂�p�����[�^�i�O�҂͏��������̂���
�Ō��܂�ϕ��萔�A��҂͋��E�����̈�j�ł����B����AT �� u1 �̊W�Ɋւ�
�Č�����ς���Au �� t �̊��Ƃ��Ă݂��Ƃ��Au(0) �� 0 �Ƃ���A
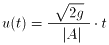 �@�@�@(����2/25)
�@�@�@(����2/25)
�ƂȂ邱�Ƃ�������܂��B

| NO.1161 | 2002.2.24. | �{���ӗ� | �}�C�i�X�̐��i�S�j |
�C�ۂ̐��E�i���v�A�ϑ��j�ł��A���̖�肪����܂��āA-1.5����
�l�̌ܓ��i�����̉��x�j��-1���ƒ�`���Ă܂��B
�܂�A�[�������ȓ_�ƊŘ��A�l�̌ܓ�����u�����v�����
�ƌ������Ƃł��ˁB
���Ȃ݂ɁA�C�ۂ̐��E�ɂ́A�Q�̂R���A�V�̂W���̃f�[�^�����Ȃ�
���s���Ă��āA�S�R�`�S�V�m�b�g�̕���V�C�}�ŕ\�����ɂ͂S�T
�m�b�g�̋L���i��H���j���g���A�S�W�`�T�Q�m�b�g�̕���\������
�͂T�O�m�b�g�̋L���ő�\�����Ă��܂��B

 E-mail
E-mail
 �߂�
�߂�