
Weekend Mathematics/コロキウム室/NO.139
| NO.1183 | 2002.4.1. | Wasmath | 続々・どちらが大きい?(1) |
63.続・どちらが大きい?の不等式を少し厳しくして,
nが自然数のとき n2n と (2n) ! ではどちらが大きいでしょうか?

| NO.1184 | 2002.4.1. | yokodon | 桁数は?(1) |
63.続・どちらが大きい?を考えていて、 以前のどこぞの大学入試で、こんなのがあったのを思い出しました。
=問題=
10210/(1010 + 3) の整数部分の桁数と1の位の数字を求めよ。
但し、321 = 10460353203 であることを用いて良い。

| NO.1185 | 2002.4.1. | teki | 桁数無制限電卓 |
前回の問題
の関係でいろいろ探して見たところ、
「桁数無制限電卓」なるものを発見しました。
1000桁程度の計算はしてくれる(桁数が大きくなると時間がか
かりますが)ようです。

| NO.1186 | 2002.4.1. | 水の流れ | 正方形の辺に色を塗る |
さて、ここに1つの正方形とn色のペンキがあります。
この4つの辺にn色のどれかのペンキを塗ります。
ただし、回転して同じになる塗り方は同一とみなします。
ただ、反転して同じになる虚像体(一方を鏡に映した像が他方になるもの)は別のものと考えます。
このとき、全体で何種類の色つき正方形ができるでしょう。
順に、設問にそって考えてください。
設問1:1色のペンキのとき。
設問2:2色のペンキのとき。
設問3:3色のペンキのとき。
設問4:4色のペンキのとき。
設問5:最後に、全体で何種類の色つき正方形ができるか。

| NO.1187 | 2002.4.1. | teki | 超累乗(1) |
今月の問題の「超累乗」ですが、
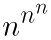 の計算順序がよくわかりません。
の計算順序がよくわかりません。
(nn)n とするのか
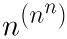 とするのかによって計算結果が全く
変わります。
とするのかによって計算結果が全く
変わります。
今月の問題の解釈は多分後者だと思いますが、数学的にはどういう規約
になっているのでしょうか?

| NO.1188 | 2002.4.2. | こざっぱ | 超累乗(2) |
n=2(つまりこの問題の場合)では、
たまたま、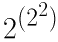 と(22)2が同じ(=16)になりますね。この問題に限っては
どちらの解釈でも答えは同じです。実際には、添字の上の方から順番に行うが正解だと思っていた
のですが、実際にはどうなのでしょうか。。。。
と(22)2が同じ(=16)になりますね。この問題に限っては
どちらの解釈でも答えは同じです。実際には、添字の上の方から順番に行うが正解だと思っていた
のですが、実際にはどうなのでしょうか。。。。

| NO.1189 | 2002.4.3. | Junko | 超累乗(3) |
「超累乗」 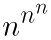 ですが、これは、
ですが、これは、
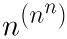 になると思います。
になると思います。
(nn)nの場合は、このようにカッコをつけるべきだと思います。
ちなみに指数法則によれば、
(nn)n =n(n・n)になるかと思います。

| NO.1190 | 2002.4.3. | Junko | 続々・どちらが大きい?(2) |
n2n と (2n) ! の大小関係ですが、
n2n > (2n) ! と予想し、これを証明します。
63.続・どちらが大きい?の時と同じ
発想でアプローチします。以下のような不等式が成り立ちます。
n2n (2n) ! n×n > (2n-1)×1 n×n > (2n-2)×2 ・・・ n×n > (n+1)×(n-1) n = n n < 2n
| n2−2(2n−1) | |
| = | n2−4n+2 |
| = | (n−2)2−2>0 (n≧4ならば) |
n>3のとき、36 >6 !
以上をまとめますと、
n≦2のとき、n2n < (2n) !
n≧3のとき、n2n > (2n) !

| NO.1191 | 2002.4.6. | Wasmath | 続々・どちらが大きい?(3) |
自然数nに対して、n2nと(2n)!の大小を比較する。
k=1,2,・・・,n−2に対して
n2>n2−k2=(n+k)(n−k)
であるから、辺々かけあわせて
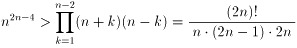
∴2(2n−1)n2n−2>(2n)! ・・・(*)
ところで、n≧4ならば
n2−2(2n−1)=(n−2)2−2>0
であるから、(*)と合わせて
n≧4 → n2n>(2n)!
n=1,2,3については直接調べると、
n=1のとき 12<2!
n=2のとき 24=16、4!=24、24<4!
n=3のとき 36=729、6!=720、36>6!
以上をまとめて
n=1,2のとき n2n<(2n)!、
n≧3のとき n2n>(2n)!

| NO.1192 | 2002.4.13. | Junko | 桁数は?(2) |
a=10210/(1010 + 3)とします。
| log10a | =log10(10210/1010 + 3) |
| <log10(10210/1010) | |
| =log1010200 | |
| =200 |
一方、321=10460353203 より、1010+3<321 従って、
| log10a | =log10(10210/1010 + 3) |
| >log10(10210/321) | |
| =log10(1010/3)21 | |
| =21(10-log103) | |
| >21(10-0.5) | |
| =199.5 | |
| >199 |
これにより、199<log10a<200 なので、
10199<a<10200 であり、従ってaの整数部分は200桁。

 E-mail
E-mail
 戻る
戻る