| NO.1526 | 2005.4.1. | FIVEILAND | 差が100の素数の組み合わせ |
毎月の問題が100回めということで、100にちなんだ問題を紹介したいとおもいます。
双子素数の応用です。双子素数は例えば11・13、41・43のように
差が2の素数の組み合わせですが、差が100の素数の組み合わせで1番小さいもの
は何でしょうか。

| NO.1527 | 2005.4.4. | 夜ふかしのつらいおじさん | 和算家の問題(2) |
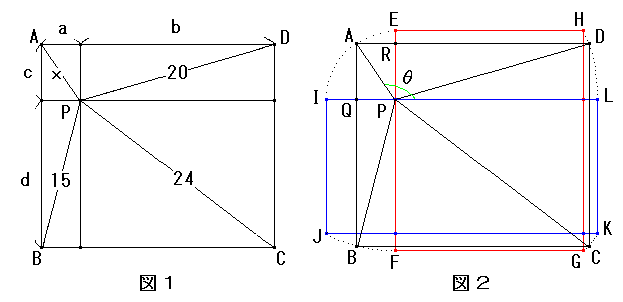
問題1:AP=7
問題2:長方形の面積の最大値は、468。
そのときのAB=20、AD=117/5。
問題3:長方形の面積の最小値は、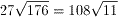
そのときのAB=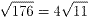 、AD=27(図2の□IJKLの場合)。
、AD=27(図2の□IJKLの場合)。
問題1 図1のようにx、a、b、c、dとします。
すると、三平方の定理より、
x2 =a2 +c2 ・・・ ①
152=a2 +d2 ・・・ ②
242= b2 +d2 ・・・ ③
202= c2+d2 ・・・ ④
①−②+③−④より
x2=49 ∴x=AP=7。
問題2・問題3 図2において∠APL=θとおきます。(θは90°から180°)
∠APL=90°のときは□EFGH、∠APL=180°のときは□IJKL。
図2で、AQ=7sinθ、AR=−7cosθ。
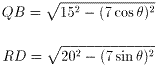
□ABCDの面積をSとおくと、
| S | =(AQ+QB)×(AR+RD) |
=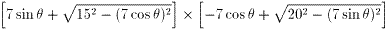
|
θで微分した導関数S' を求め整理すると、
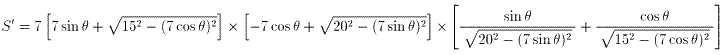
ここで、S' の1番目と2番目の[ ]の積を考えると常に正。
(理由1、Sと同じ式だから)
(理由2、最初の[ ]の中が一番小さくなるのは、θ=180°のときなので、
sinθ=0、cosθ=−1を代入してみると、
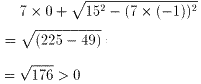 ・・・ 図2のIJの長さ
・・・ 図2のIJの長さ
2番目の[ ]の中が一番小さくなるのは、θ=90°のと
きなので、sinθ=1、cosθ=0を代入してみると、
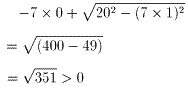 ・・・ 図2のEHの長さともに正なので、積も正。)
・・・ 図2のEHの長さともに正なので、積も正。)
よって3番目の[ ]の値を0(零)とするθを調べると、tanθ=−4/3。
このとき、sinθ=4/5、cosθ=−3/5。
このθの値をαで表すと、
| θ | 90° | ・・・ | α | ・・・ | 180° |
|---|---|---|---|---|---|
| S' | + | 0 | − | ||
| S | 増加 | 468(最大) | 減少 |
θ=180°のときが最小値になります。(図2の□IJKL)

| NO.1528 | 2005.4.9. | 佐野允信 | 和算家の問題(3) |
(1)AB=b,BC=a とおく。
xy座標を考え、点A,B,C,Dの座標をそれぞれ、(0,b),(0,0),(a,0),(a,b)とし、
点Pの座標を(x,y)とする。
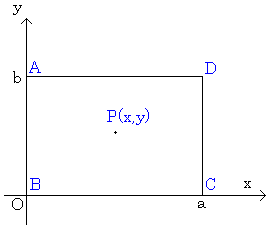
BP=15より、
x2+y2=152 ・・・(1)
CP=24より、
(x-a)2+y2=242 ・・・(2)
DP=20より、
(x-a)2+(y-b)2=202 ・・・(3)
さらに、
x2+(y-b)2=AP2 ・・・(4)
(3)-(2)より
(y-b)2-y2=202-242 ・・・(5)
(1)+(5)より
x2+(y-b)2=152+202-242=72 ・・・(6)
(4)(6)より
AP2=72
∴ AP=7 −(答)
(2)と(3)
長方形ABCDの面積をSとおくと
S=ab ・・・(7)
(2)-(1)より
| (x-a)2-x2=242-152 | |
| ←→ | a2-2ax-351=0 |
| ←→ | (a-x)2=x2+351 |
a-x≧0より
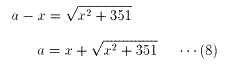
(5)より
| b2-2by+176=0 | |
| ←→ | (b-y)2=y2-176 |
(b-y)2≧0より
y2-176≧0より
y≧0より、
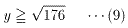
b-y≧0より、
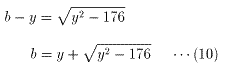
(1)より、
x2=225-y2
x2≧0より、225-y2≧0
y≧0より、0≦y≦15 ・・・(11)
(9)(11)より、
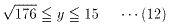
x≧0より
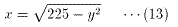
(13)を(8)に代入すると
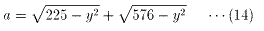
(7)に(10)と(14)を代入すると
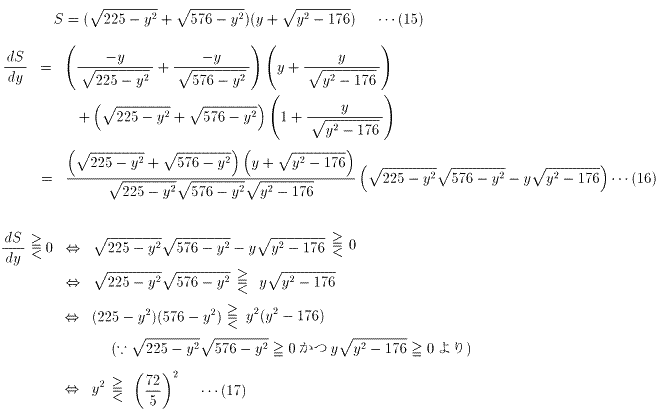
よって、
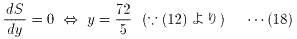
増減表は下図のようになる。
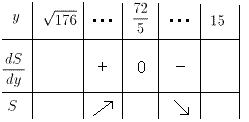
(15)より、
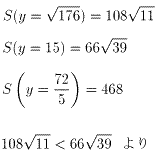
長方形ABCDの面積は、
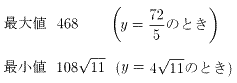
をとる。

以上より、長方形ABCDの面積は
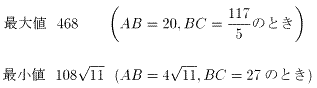
をとる。 −(答)

| NO.1529 | 2005.4.9. | DDT | 何故πは3.141592・・・ |
先日息子が、中学校の職員室のほぼ全員の期待を裏切って、某公立の新設理数系に推薦で受かってしまいました。舞い上がった息子は、私にこんな質問をぶつけてきたのです。
「なんでπ = 3.141592・・・なんだ?」そのとき酩酊状態にあった私は、すごく焦りました。それは、これが次のような質問だと思ったからです。
1.普遍(?)定数2
例えば、万有引力場を考えます。Fを重力,重力定数をG,重力源の質量をm,mからの距離をrとして、
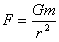
となります。ここで右辺分母のrの指数2に注目してみます。rの指数は何故2なのでしょう?。それは重力源を中心とした半径rの球の表面積がr2に比例するからで、そこを貫く力線の数が一定だからです。これは一種の流量保存則であり、単位湧き出しを仮定した流体力学においても、単位湧き出しの流量は一定なので、そこからr離れた地点での流量密度はr2に逆比例します。
このように考えると、rの指数2は一種の普遍定数です。それは球の内的な幾何学的性質のみで決まります。「なんでπ = 3.141592・・・なんだ?」は、最初こういう類の質問かと思って肝を冷やしました。明らかにπも一種の普遍定数です。それは空間の平坦性に関連してるから、ミンコフスキーの計量構造の話になる・・・。もっといえば接続係数がどうのこうのの・・・・・・「ワタシャそこまでは知りませんよ・・・」。
でも実際には、たんにπ = 3.141592・・・となる計算過程が知りたいだけだと、すぐに判明しました。πの値を計算するには、単位円の周長を計算すれば良いはずです。私は息を吹き返し、次のように言いました。
「そんなもの積分計算で1分で出してやる!(たまには親爺の偉大さを思い知れ!)」
2.大馬鹿者
| 親爺: | 「いいか、曲線長を計算するには線素を積分すればいいんだ!」 |
| 息子: | 「?」 |
| 親爺: | 「(知らないかもしれないが)極座標ってのがあって、そこでは単位円は
って表せるんだ!」 |
| 息子: | 「??!」 |
| 親爺: | 「それで、これらをθで微分して線素を求めれば、
となるから・・・」 |
| 息子: | 「・・・」(すでに勝手にやればモード) |
| 親爺: | 「単位円の周長は、dsを積分して、
となる。だから単位円の周長は2πだ!」(あれっ?。なんか変だな?) |
| 息子: | 「んでっ?、これのどこが π = 3.141592・・・ の計算なんだい?」
(すごく優しい声だった・・・) 1分くらい放心したのち、次のように言いました。 |
| 親爺: | 「いや〜!。久々なので間違っちゃったよ〜!。」 |
| 親爺: | 「じつはな、tanφの逆関数があってな、それのテーラー展開を使えば・・・」 |
・・・でも何故、式(1)で具体的な単位円の周長の数値を計算できないのでしょう?。これは明らかなことなのかも知れませんが、私にとっては、とても不思議なことでした。明快な理由を思いつけなかったからです。どなたか教えて頂けないでしょうか?。

| NO.1530 | 2005.4.10. | DDT | 量子力学が思ったほど奇妙でないわけ(3) |
先日NO.1491で、相当にかっとんだ事を書いてしまいましたので、お詫びに以下の本を紹介したいと思います。この本の出自だけは確かと思えますので、お詫びになってればと願うのですが・・・。
種本は「量子力学の奇妙なところが思ったほど奇妙でないわけ,デヴィッド・リンドリー,青土社,1997年」です。
1.前回までのまとめ
1) 量子力学の認識論を実験事実に基づき提出したニールス・ボーアは、「自然は非局所的存在である」ことと「自然は確率的的存在である」を提唱した。
2) 同じ実験事実を認めていたアルバート・アインシュタインは、しかし、常識的考えに基づき、そのようにみえることを説明する隠れたパラメータ理論を望んだ。アインシュタインにとっては、「自然は確率的存在でなく」そうみえる原因は、「自然の見かけ上の非局所性」だった。つまり、「自然の見かけ上の非局所性」を解決できれば、「自然の見かけ上の確率性」も解決できるはずだった。
3) しかしそれは、ベル−アスペの実験が否定した。アインシュタインが望んだような、「自然の見かけ上の非局所性」があったとしても、それとは独立に「自然は確率的存在」であることが実証された。
4) 従って、我々は量子力学の観測問題に直面せざる得ない。その象徴的例は「シュレーディンガーの猫」である。量子力学の基礎方程式であるシュレーディンガー方程式と、そのボルン−ボーアのコペンハーゲン確率解釈を信じる限り、量子的不確定状態に1対1に対応させられた巨視的な「猫の生死」は、「生きてもいるし同時に死んでもいる状態」になりうる。
2.キーワードは「コヒーレント」
ここからのキーワードは「コヒーレント」になります。「コヒーレント」とはもともと、幾つかの光源から発射された光に対して、それらの位相が揃っている場合に使われた言葉だと思います。よって拡張解釈すれば「コヒーレント」とは、「足並み揃った」とか「ベクトルの揃った」とかの意味にとれます。
3-1.コヒーレント其の1,レーザー光線
では最初の例です。もともとの語源である光に対する例でいうと、「コヒーレント光」とはもちろんレーザー光線が代表です。ヘリウムレーザーの発生手順は、以下のようなものです。
① ヘリウムを真空管に閉じ込め、真空管の電極を使って電圧をかけ、ヘリウムの電子が後1歩で光子を放出するくらいの、ぎりぎりの励起状態に追い詰めておく。ヘリウム分子はその状態では、ヘリウム原子に解離している。
② 1個のヘリウム原子に、その電子が光子を放出するような、とどめの一撃を与える(何らかの方法で)。
③ 一撃された原子の電子は、ボーアの前期量子論に従って、ある一定の波長と位相とを持つ光子を放ち、安定軌道へと落ちる。
④ 放たれた光子は、ほとんどタイムラグ0で、隣のヘリウム原子の電子を叩く。叩かれた隣のヘリウム原子の電子は、叩かれた瞬間に、叩いた光子と同じ波長と位相を持つ光子を放つ(誘導放射)。そして電子は、安定軌道へと落ちる。
⑤ 真空管内の全てのヘリウム原子の電子は臨界励起状態にあるために、以上の誘導放射の連鎖反応が起こり、真空管内のヘリウム原子全体がほぼ一斉に、同一波長と同一位相とを持つ光子を放出する。
⑥ 結果として、それらの光子の重ね合わせで「コヒーレント光」である「レーザー光線」が得られる。それは、同一位相の(足並み揃った)光子の(光波の)足し算なので、足し算の結果は非常に強力な光線となり、レーザートーチは分厚い鉄板さえ切り裂くことになる。
ここで重要なのは、電圧をかけて、ヘリウム原子の電子が後1歩で光子を放出するくらいの、ぎりぎりの励起状態にまで一様に追い込んでおくことです。全てのヘリウム原子が臨界励起状態になければ、どれか一個の原子の電子が光子を放出しても、その光子は隣の原子の電子に食われるだけで、隣の原子の電子は誘導放射を起こしません。誘導放射の連鎖反応を惹き起こすためには、まわり中の全ての原子の電子が臨界励起状態になければいけません。まわり中の全ての原子の電子を臨界励起状態にするためには、ヘリウム分子が原子に解離するくらいの電圧が必要です。電圧とは、位置ポテンシャルエネルギーのことです。ということは「レーザー光線」という「コヒーレント光」を得るためには、当たり前かもしれませんが、けっこうなエネルギーが必要です。これが、「エネルギーとコヒーレント成立」の最初の例です。
3-2.コヒーレント其の2,2重スリット実験
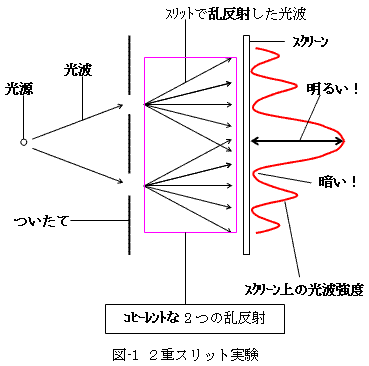 古典的な2重スリット実験とは、右図のようなものです。1つの光源から放射された光波は、ついたての2重スリットによって乱反射されます。2つのスリットで乱反射された光波ですが、それらは同じ光源から放射されたので、位相が揃っています。つまりコヒーレントです。よってその後ろのスクリーン上では、乱反射の光学的距離に従って、2つ乱反射光は、明るい部分と暗い部分の干渉縞をつくります。これは、光が波動そのものであると思われていた実験事実そのものです。
古典的な2重スリット実験とは、右図のようなものです。1つの光源から放射された光波は、ついたての2重スリットによって乱反射されます。2つのスリットで乱反射された光波ですが、それらは同じ光源から放射されたので、位相が揃っています。つまりコヒーレントです。よってその後ろのスクリーン上では、乱反射の光学的距離に従って、2つ乱反射光は、明るい部分と暗い部分の干渉縞をつくります。これは、光が波動そのものであると思われていた実験事実そのものです。
じつは、電子ビームに対しても同じことが成り立ちます。電子ビームを2重スリットを持った「ついたて」にぶつけた場合、スクリーンである蛍光板には、光波と同じような干渉縞が現れます。
この場合、2重スリットとは結晶格子です。結晶の格子配列の姿を確かめるために、光波であるX線回折技術が開発されたのですが、その後、電子ビームを用いた電子回折実験も行われました。光波を用いても、電子ビームを用いても、一つの結晶格子の姿に対しては同等な干渉縞が得られ、同じ結論が得られます。つまり粒子そのものと思われていた電子が、光波のように振舞います。そこでは図-1の乱反射光が、スリットで乱反射された電子の確率波動場におきかわります。2つのスリットで乱反射された確率波動場は、同じ電源(?)から放射された1個の電子に関するものなのでコヒーレントな関係にあり、コヒーレントな乱反射光と同じ事情がなりたって、スクリーン(蛍光板)上の電子の存在確率強度に干渉縞が生じます。ただし注意すべきは、1個の電子がスクリーンに衝突しても、その結果は輝点となるだけで、縞にはならないことです。前回述べたように確率波動場は決して観測できないため、その干渉も直接見ることはできません。ただし多数の電子を次々とぶつけていくと、干渉効果の結果はみれます。それがスクリーン上の縞模様となって現れます。
同様に、1つの光源から発射された1個の光子については、干渉縞が存在しないことにも注意すべきです。図-1のような実験を行う場合、多数の光子を1度に放射するために、通常このことには気づきません。「種本」のpp.61〜62には、このことが非常にヴィヴィッドに描写されています。そして光子に対して、ファインマンの経路積分法を適用すれば、ついたてとスクリーン間の光波の強度分布も再現でき、それはマックスウェル方程式から予想されるものに(通常我々が目にするものに)一致すると思えます。このようにして、量子効果は表面上古典論と(日常経験と)何一つ矛盾しないことが、再び示されます。
すいません。ここからが本題です。ここでは「コヒーレント性は易々と崩せること」をいいたいのです。図-2のような状況を考えます。
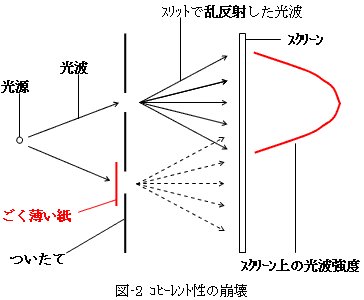 図-2のような状況では、純粋に古典的に光波を考えても干渉縞はもはや得られません。ごく薄い紙1枚が、干渉縞を生成する一方のスリットを抜けるべき光波を阻むからです。スクリーン上の光波強度には強弱がつかず、干渉縞も現れません。干渉縞は、位相の揃った2つの光波の重ね合わせから生まれます。このことは、たとえ紙を透過した光があったとしても、紙の阻害効果が大きすぎて、2つの乱反射光は、もはやコヒーレントな関係にないことを意味します。
図-2のような状況では、純粋に古典的に光波を考えても干渉縞はもはや得られません。ごく薄い紙1枚が、干渉縞を生成する一方のスリットを抜けるべき光波を阻むからです。スクリーン上の光波強度には強弱がつかず、干渉縞も現れません。干渉縞は、位相の揃った2つの光波の重ね合わせから生まれます。このことは、たとえ紙を透過した光があったとしても、紙の阻害効果が大きすぎて、2つの乱反射光は、もはやコヒーレントな関係にないことを意味します。
これを光子や電子の確率波動場におきかえて考えてみます。紙がない場合、1つの光子や電子は、上下スリットを50%の確率で同時に抜ける状態にあります。だから確率波動場の干渉が起きます。では、1つの光子や電子は、上下スリットのどちらを抜けたのでしょう?。それを確認するには、例えば下スリットの前に紙という検知器を置けば確認できます。ところが、1つの光子や電子が紙に衝突したということは、紙という検知器への、確率波束の収束をもたらします。つまりその瞬間、上スリットを抜ける確率波動場も消滅し、上下スリットを同等に通り抜ける2つの確率波動場というコヒーレント状態も消滅します。スリットの前に紙をおくということは、じつは量子の位置確認実験になっています。このような実験によって確率波動場は原理的に観測できません。その理由が確率波束の収束であり、それは確率波動場のコヒーレント性を破ることにもなります。
ところがコヒーレント性を保つ方法があります。エネルギーをつぎ込めば良いのです。ごく薄い紙1枚を突き抜けるくらい強力な光源を用いれば、最初のものと多少違うかもしれませんが、再び干渉模様を得られるはずです。こうして、「エネルギーとコヒーレント成立」の第二の例に出会えます。そしてこの関係は、古典的に考えても、量子的に考えても現実に同じ効果をもたらします。
3-3.コヒーレント其の3,巨大な量子系
「種本」によれば、現在では直径数センチの超伝導リングを維持できるそうです。超伝導リングとは、その中を電流が抵抗0で永遠に流れ続けるために、電気備蓄装置に使えないかと一時本気で議論された、あの超伝導リングです(バブルな時代でした)。
超伝導リングの中の電流は、周方向に沿って一様な電子の流れであるため、全ての電子の足並みが揃っています。つまりコヒーレントです。このときの電子集団の状態は、模式的に考えると、前回のボーアの量子条件で述べたような水素原子の電子の状態です。水素原子の電子は、その波長の整数倍が周回軌道の周長に等しいような定常波として存在します。ただし水素原子の電子は1個の電子ですが、超伝導リングでは、これが電流となっている電子集団全体に対して概ね成立します。
超伝導リングに少々手を加えると、流れる電流の強さをコヒーレント状態を保ったまま変化させられます。このとき何が起こるでしょう?。超伝導リングの電子集団は、波長の整数倍が周回軌道の周長に等しいような定常波です。電子の波長は、プランク定数hに比例するとびとびの値です。しかもリングの周長は一定です。よって定常波の波数もとびとびの値にならざる得ません。定常波の波数は、流れる電流の強さに対応します。つまり超伝導リングにおいては、そこを流れる電流の強さが離散化され、連続的に変化することができません。可能な電流の強さは、量子力学が予想するとおりになります。
直径数センチの超伝導リングは、量子状態を担う電子に比べれば非常に巨大なものです。量子効果は、ミクロな素粒子レベルの、しかも素粒子1個1個についての話であり、巨視的な日常世界には決して現れないというのが、伝統的な量子効果解釈でした。伝統的な観測問題の解決も、そこに逃げ場を求めています。極微の量子系は、巨視的な観測装置と相互作用した時に観測が成立し粒子となる、というのがそれです。しかし金と時間さえかければ、直径数センチの超伝導リングは、直径数キロの超伝導リング電気備蓄基地に変えられます。そこでは人が感電死するくらいの巨視的な電流が(巨視的な電子集団が)コヒーレント状態を保ったまま、巨視的な量子状態にあります。この例は、伝統的な観測問題の解決が、現実に嘘であることを実証しています(非常に地味ですけど)。これが「エネルギーとコヒーレント成立」の第三の例です。
超伝導リングを維持するには、伝導リングを極低温に冷やしておく必要があります。極低温状態は非常に不安定なもので、ほっとけばリングはすぐに暖められ、極低温状態もコヒーレント状態も(超伝導状態も)すぐに崩壊します。抵抗が現れれば、あちこちで電子は原子核に衝突し出し、その足並みはばらばらに崩れて、あらゆる電流値をほぼ連続的に取れるようになりますが、同時に減衰していきます。しかし極低温です。どこにエネルギーをつぎ込んだのでしょう?。極低温の維持にエネルギーをつぎ込んでいます。
直径数キロの超伝導リングを維持するための冷却材として、液体ヘリウムを使ったとします。液体ヘリウムを製造するためには、莫大な圧力を(エネルギーを)常温ヘリウムにかけて断熱膨張させます。直径数キロ分ともなると、それも半端な量ではないはずです。また超伝導リングの維持は、巨大な冷蔵庫と同じですから、そうやって製造した液体ヘリウムをリングのまわりに循環させる、数キロ分の熱交換器とコンプレッサーも必要です。結局それらは膨大な電力を消費し、発電所はせっせと石油・石炭を焚くわけです。こんなことが真面目に議論された20年前は、やっぱりバブルだったんだと思います。
3-4.コヒーレント其の4,古典的コヒーレント嫌い(熱運動)
以下は「種本」のpp.205〜222について、個人的に思うことを述べました。
よくいわれることですが、沸騰したヤカンのお湯は冷めるだけで、いったん冷めたお湯が、自然に沸き戻ることはありません。本当にそうでしょうか?。お湯の分子レベルまで降りて、分子1個1個に対する運動方程式をたてることは、原理的には可能です。熱現象とは、お湯の分子運動が原因なので、その運動方程式の解が、お湯の冷めてゆく過程を表します。ところが運動方程式は時間反転が可能です。お湯が冷めてゆく過程が運動方程式より可能なら、その解の時間を反転した、お湯が温まってゆく過程も同じ運動方程式の解となります。これは、いったん冷めたお湯が、自然に沸き戻ることを意味します。
現実にありえないような解が数学的操作から生じた場合、そのような解は、物理的制約条件から無縁根となるのが普通です。例えば、運動量保存則とエネルギー保存則を連立させて、2質点の完全弾性衝突を解いた場合、エネルギー保存則は2次方程式なので、2組の可能な解が生じますが、一方の解は質量が負でなければ成立しない解なので、そちらは無縁根として捨てられます。しかし、お湯が自然に沸き戻る過程を表す解は、運動方程式の時間反転性に基づくものなので、このような制約が一切ありません。つまりそれは現実に可能なのです。このパラドックスは19世紀に議論され、ボルツマンの統計力学が登場します。ボルツマンの統計力学では、次のように考えます。
お湯が自然に沸き戻る過程は現実に可能であるが、運動方程式の具体的解の決定には、初期条件が必要である。ほっとかれたお湯が自然に沸き戻るような初期条件は、確率的にはほとんど成立しない。どれくらい低いかというと、それが偶然に実現するには、宇宙の年齢以上の時間が必要だ。
冷めたお湯が沸き戻るためには、ある瞬間にお湯の全分子運動の方向が反転する必要があります。それを初期条件として運動方程式を解けば、確かにお湯は沸騰状態に戻ります。しかし、お湯の全分子の運動が、ある瞬間に一斉に反転することは、めったにありません。「ある瞬間の一斉反転」とは、一種のコヒーレントです。コヒーレント成立のためにはエネルギーが必要でした。実際にそうしてるじゃないですか!。それがヤカンをコンロにかける、という行為です。熱エネルギーという形で、お湯にエネルギーを与えています。
ただし熱エネルギーは、この世で最も効率の悪いエネルギーです。熱エネルギーの指標は温度です。統計力学によれば、温度とは分子や原子集団の運動エネルギーの平均値です。運動エネルギーの平均操作を具体的に考えてみると、次のようになります。
熱運動をしている粒子の運動量ベクトルは、ほぼ完全なランダム状態にあります(統計力学の前提)。平均操作とは足し算なので、ランダムな運動量ベクトルを集計すれば、てんでばらばらな方向のベクトルが打ち消しあって、足し算の結果は、その残り滓にすぎません。しかも平均なので、その残り滓を全粒子数(膨大な数です)で割ります。この残り滓は粒子全ての運動量ベクトルの和なので、確かに全粒子運動の足並みの揃い踏み部分です。つまり粒子集団全体のコヒーレント性を表す量であり、それが温度です。熱エネルギーによって温めるとは、その残り滓程度の効果で、徐々に平均的にコヒーレントを高めてゆく過程です。
3-5.コヒーレント其の5,古典的コヒーレント嫌い(エントロピー増大則)
熱エネルギーの効率の悪さは、そのランダム性に起因します。では、何故熱エネルギーはランダムなのでしょう?。そこには古代から中世、中世から近世・近代そして現代にいたる過程で徐々に形成され受け継がれてきた、あるエッセンスが含まれています。
がそれです。これに近世〜近代において形成されてきた原子論と、ニュートン力学の力学的エネルギー保存則を結びつけます。
となります。無目的とは今の場合ランダムと同義であり、これは、熱運動状態がこの世界の普遍的状態だ!、といってるのと同じです。つまり、自然は低レベルエネルギー状態(低コヒーレント状態)を保つ、巨大な恒温槽なのです。ふと周りを見回すと、確かにそうです。
自然界のコヒーレント性の代表は台風です。台風とは、高エネルギー高速度かつ、巨視的に風向が揃った巨大なコヒーレントです。でもそれは蒸し暑い熱エネルギーの塊でもあります。ということは非常に無駄も多いというか、現実には途方もない無駄の上に、そのコヒーレント性が成立しています。
台風で大気は莫大なエネルギーを暴発させます。暴発したエネルギーは、家屋を倒壊させ、ダムや堤防を決壊させて洪水を起こし、津波や高潮を起こします。結果として残るのはほぼ完全なランダムです。巨大なコヒーレントが恒温槽に食われたのです。日本のエントロピーが、台風によって増加したといっても同じです。
もっと単純な例として室内の大気を理想気体と考えます。そこに扇風機で風を送ります。風とは運動ベクトルの揃ったコヒーレント状態です。風の分子は、大気の分子と衝突しますが、そのぶつかり方はどうなるでしょう?。例えば1個の風分子が、たまたまその運動方向に飛んでいた大気分子と正面衝突し、運動ベクトルが反転するということはあり得ます。そのような現象が全風分子に対して一斉に起これば、風は扇風機への逆風となりますが、そのようなことが起こるためには、大気がもともと逆風状態というコヒーレント状態になければなりません。しかし現実には、大気は低コヒーレントな恒温槽なのでランダム運動が支配的です。大気が偶然に逆風状態になる確率は0ではありませんが、その実現には「宇宙の年齢以上の時間が必要」になります。
したがって風分子は大気からランダムな衝突を受け、風分子集団のコヒーレント性(運動ベクトルの斉一性)は散逸していきます。同時に、大気より相対的に高かったその運動エネルギーも、大気の全分子へ平均的に分配されて散逸し、恒温槽のランダム性が回復されます。力学的エネルギー保存則は守られたままの状態で。
このように、いったん自然を巨大な恒温槽とみなせば、統計法則としてエントロピー増大則は、ほぼ不可避的に出てきます。この事情は、古典論であろうと量子論であろうと同じであるはずです。その理由は、その本質が統計理論だからです。いってしまえば、その本質が物理法則とは無関係だからです。このことの意味は重大です。じつは古典論においても、自然が確率的存在であることは、実証されていたのです。ただしその確率性の由来は、古典論でははっきりしています。アインシュタインは、「隠れたパラメータ理論」にこのような明快さを求めたのだと思います。いずれにしろ、コヒーレント性は自然に散逸する、といえそうです。
4.新しい物質像(コヒーレント理論)
量子に対して、コヒーレントの自然散逸が起こるかどうかを、定性的に考えてみます。1個の電子を考えます。1個の電子は、まさにコヒーレント状態そのものです。電子の存在確率は、全空間に同時にコヒーレントに拡がっています。全宇宙にこの電子1個しか存在しないのならば、電子の位置はまるでわからないのかも知れません。そこで仮定(2)の量子力学版を持ち込みます。全空間には電子の確率場の他に、多数の光子や原子核の確率場が、ランダムに存在します。しかもそれらもコヒーレントに全空間に拡がっています。
先の電子と、光子や原子核はどこかで相互作用を起こすと思われます。相互作用しないのは、電子・光子・原子核の3者が、最初からコヒーレント状態にある場合のみです。そのようになる確率は0ではありませんが、自然のランダム性のために、ほとんど実現性がありません(宇宙の年齢以上の時間が必要)。相互作用とは衝突することを意味します。
衝突地点が100万光年彼方である確率も0ではありませんが、それぞれの確率場の最も濃い部分で衝突する確率が最大です。つまり電子は、手近な光子と衝突します。衝突とは位置の確定です。このとき波束の収縮が起こり、電子と光子のそれ自身のコヒーレント性が破れます。これは、自然がまさに自然に行っている量子の位置確認実験です。
次のような描像が可能になります。最初全空間に拡がっていた電子は光子に衝突し、位置が確定します。相互作用が終了し、双方が飛び離れると、再び電子は全空間に拡がります。そして次の原子核と衝突し・・・。このように繰り返しコヒーレント性が破れて位置が確定してゆく過程を、巨視的系に属する人間が観測したら、どう見えるでしょう?。電子の衝突相手は、そこらじゅうにランダムにいるので、位置確定はほぼ連続的にみえます。その軌跡は経路積分法による結果と一致するはずです。経路積分法は、それが古典論の結果と一致することを保障します。古典論の結果とは、電子の古典的粒子軌道のことです。やっと現実の世界に還ることができました。
しかし自然のランダム性によるコヒーレントの破れがなかったら、この世界は確定しないことにもなります。例えば首都高速道路だって、原理的にはシュレーディンガー方程式に支配され、その存在確率は全空間に拡がっているはずです。首都高がそこにあり続けるのは、それ自身のランダム熱運動が、自動車の粉塵や排気ガスが、大気の熱運動が、さらには太陽や星座の光や宇宙線が、首都高の確率場と衝突し続けて位置を確定し続けるからであり、自然がまさに自然に行っている量子の位置確認実験が、常に起きているからだ、ということにもなります。
5.観測問題の解決
ここまでくれば、観測問題は定性的には解決できます。「シュレーディンガーの猫」問題を解決しましょう。
50%の確率でシュテルン・ゲルラハ実験の右電子が、電子検知器に飛び込みました。電子検知器は、2つの量子状態を同時に持てます。一方は電気信号を流さない(電子はこなかった = 生きた猫)であり、他方は電気信号を流す(電子はきた = 死んだ猫)です。この不確定状態は1瞬だけなら存在するかも知れませんが、電子は手近な物体と衝突する確率が、べらぼうに高いのです。生きた猫状態と死んだ猫状態のコヒーレントは、絶対といって良いほどの確率で、死んだ猫状態へと破れます。電子検知器が発した電気信号の電子も、ボーガントリガーに届かない確率は持っています。しかしそのコヒーレント状態も、電線の抵抗作用が電子の位置確認実験を行い、電子の位置は確定して、電流が流れる状態へとほぼ絶対に破れます。以下同様です。たとえ箱の蓋を開けなくても、「猫は死んだ」と言い切れます。電子検知器に電子が飛び込んだ瞬間が、やはり観測の成立時だったのです。
前回と今回で何が違うかというと、「自然界におけるコヒーレント性の自然散逸」を認めることによって、「これらの過程は、電子・検知器・電線・ボーガン・箱・矢・箱の中の空気・猫を構成する全ての原子核および電子のシュレーディンガー方程式を連立させて解けば、原理的には説明できるはずだ!」と、かなりの自信をもって言うことができる点です。
6.解決されそうな問題、解決されなかった問題
さきほどの多粒子系シュレーディンガー方程式の話ですが、もちろん解いた人は誰もいません。現在のところスパコンを使っても無理です。単純な化学反応の多粒子系シュレーディンガー方程式さえ解けないために、福井先生が「フロンティア電子軌道理論」でノーベル賞をとったくらいです。ただ本当にこれが、量に起因する複雑さの問題だけであるならば、古典力学のある問題を連想させます。太陽系の生成問題です。
ニュートンの古典力学は17世紀の産物ですが、その1世紀後には「太陽系がガス雲の渦巻きから万有引力の法則のみで現在の姿に凝集した」という説が、少なくとも知識人の間では定説になっていました。19世紀や20世紀ともなると、その説は一般大衆の常識にもなりましたが、つい最近まで、誰も数値計算で確認した人はいなかったのです。実際ニュートンはたったの3体問題で苦労し、多体問題の難しさから「ガス雲の渦巻きから万有引力のみで」太陽系が生成されるなどということはあり得ない、と考えるようになりました。太陽系の生成が数値シミュレーション可能になったのは、1980年代も後半のことです。この分野では日本の数値天文学者達が理論的にも大活躍したのですが、最大の原因はスーパーコンピューターがふんだんに使えるようになった、計算環境の進化でした。シュレーディンガー猫方程式は、太陽系生成問題と比べても桁違いの難しさと思えますが、それがあくまで量の問題なら、計算環境の進化が解決してくれるはずです。量子CPUです。
一方、解決されなかった問題もあります。「自然が確率的存在」であり「非局所性」を持つ理由は、いまもって誰も知りません。次のような可能性が否定されたわけではないのです。
量子の確率場の干渉や波束の収縮を直接見ることはできませんが、3-2で述べたように多数の実験を行えば、その結果を見ることは可能です。例えば100万匹のシュレーディンガーの猫を使い、実験装置を超伝導状態に維持して実験を行って(つまりエネルギーをつぎ込んで)、実験終了後に猫をゆっくり解凍したら、猫の生死の確率場の干渉結果として、血の海の中に元気な猫が茫然自失していたなどという可能性は、あいかわらず否定されていません。
7.再びヤマト世代
前期量子論全盛の頃、正準方程式という名の古典力学の奥義が、天体力学分野の片隅から引っ張り出され、一躍脚光を浴びました。正準方程式は運動方程式の理論的整備の華といえますが、例えばそこでは位置と運動量は正準共役と呼ばれる関係にあります。量子力学において、位置と運動量には不確定性関係が成立します。シュレーディンガー方程式が出るまでは、正準方程式で共役関係にある物理量に不確定性関係が成立するということが、古典論を量子化する唯一つの一般的方法でした。そして時間とエネルギーは、この共役関係にあります。時間とエネルギーには、不確定性関係が成立します。ということは、素粒子は空間的にワープするどころか、そこらじゅうでタイムワープしている可能性があります。これが全くの嘘ではないかもしれないことは、ベータ崩壊現象で確認されています。
通常の条件下では存在しない粒子も加速器の中では造れます。その粒子は不安定なのですぐに崩壊し、いくつかの素粒子に分裂します。このとき崩壊前後の質量収支がどうしても合わない例が発見されました。質量保存則は後期量子論の段階でも絶対法則でした。そこに登場した湯川秀樹は、時間とエネルギーの不確定性関係に目をつけました。相対論によれば、質量とはエネルギーの一形態です。だとすれば、時間とエネルギーの不確定性から、一瞬ならば質量保存則も破れていいのではないか?。この効果を考慮して彼は新粒子を予測します。それが湯川の中間子です(またまたノーベル賞です)。
一瞬でも質量保存則が破れるということは、ときどきなら全宇宙の質量も変化してよろしいということです。欠損質量は過去や未来に飛んで行ってるのかもしれません。あるいはその逆かも。ときどき特集される「世界の超常現象」の本当の原因は、じつは巨視的な量子効果だったりして・・・。莫大なエネルギーとの引き換えなしに巨視的な量子効果を得る確率はほぼ0ですが、宇宙の年齢以上の時間と言ったって確率は確率です。起きないとは限りません。こんなことを考えていると、ガミラスの宇宙魚雷を虚空へ消えつつかわすヤマトの姿が蘇ります(ワープです)。「ワープ9の高速で!」と叫ぶカーク船長も。かつて「新しいアインシュタイン」と唱われたリー・スモーリンは、その著書「量子宇宙への3つの道(草思社2002年)」で、早くて2015年までに量子力学の謎は解明され、21世紀の終わりまでには高校で量子重力理論が教えられていると言い切ります。大学で坊さんの資格を持っていた教授が、こんなことを言っていたのを思い出します。
「星占いは、古代から中世の数千年をかけて蓄積された統計資料に基づいている。だからそれは嘘じゃない。嘘じゃないけど、現代の時代変化は、その数千年より遥かに速いから、占星術は当たらない」
一瞬本当かもしれないと思いました。「映像で見る20世紀」を思い出せば、前世紀の時代変化がどれ程の速さであったかがわかります。21世紀になって「空中都市008」のようにエアカーが走り回る時代は来なかったけれど、ハイブリッドカーはついに実用化され、「タイムトンネル」や「原潜シービュー号」の磁気テープ式電子頭脳より、目の前のパソコンのほうがよっぽど性能が良さそうな時代は、確かに来ました。ひねくれて考えれば、ソ連の崩壊は「資本論」と「マックス・ウェーバー」の正しさの証明だったのかも知れません。酩酊状態で、生きてるうちに火星くらいまではワープできる時代がこないかなと、ときどき思います。
とりあえずは10年後の2015年です。リー・スモーリンさん。よろしくお願いします。

| NO.1531 | 2005.4.18. | Kernighan | 何故πは3.141592・・・(2) |
一部訂正(4/19,21:00)
NO.1529 何故πは3.141592・・・
が面白かったので考えてみました。
一般的に曲線は
c(t):[0, 1]->(x(t), y(t))
とあらわされて、この曲線の長さは
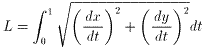
で求められます。
ところでこの曲線を別のパラメータsであらわすことにします。
(曲線の弧長表示)
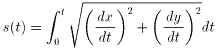
c(s):[0,L]->(x(s), y(s))
そのときの曲線の長さlは
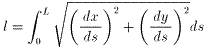
ですが
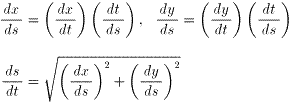
なので
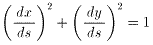
となって
という自明な結果になります。
つまり(cosθ,sinθ)(θはラジアン)は円の弧長表示なので
自明な結果しか得られないということだと思います。

| NO.1532 | 2005.4.24. | 水の流れ | ピックの公式 |
皆さん、多角形の面積を求める素晴らしい公式を紹介します。 ここでは、手順にしたがって、証明していきます。
|
公式:すべての頂点が格子点にある多角形が、内部にa個の格子点をもち、周上にb個の格子点をもつとき、その面積は 格子の間隔を1とすると、 a+(b/2)−1 である。 |
手順1:格子の線上に4辺がある長方形のとき、ピックの公式を証明せよ。
手順2:格子の線上に直角をはさむ2辺がある直角三角形のとき、ピックの公式を証明せよ。
手順3:多角形Aが2つの多角形B,Cに分割されるとき(その1)
多角形B,Cに対してピックの公式が成り立つならばAに対しても成り立つことを証明せよ。
手順4:多角形Aが2つの多角形B,Cに分割されるとき(その1)
多角形A,Bに対してピックの公式が成り立つならばCに対しても成り立つことを証明せよ。
手順5:格子点上に頂点をもつ一般の三角形のとき、三角形の頂点を通り、4辺が格子線上にある図のような長方形を考える。
この図を利用して、ピックの公式を証明せよ。(文章表現になる)
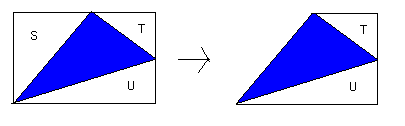
点順6:格子点を結んでできる一般の多角形のとき、ピックの公式を証明せよ。(文章表現になる)
<問題の出典:中高一貫数学コース「数学Ⅰをたのしむ」志賀浩二著 岩波書店>

| NO.1533 | 2005.4.25. | 夜ふかしのつらいおじさん | ピックの公式(2) |
手順1
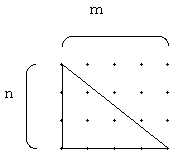
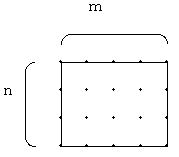 左の図のように横・縦の長さがm・nの長方形の格子点を考える。内部の点の個数をa、周上の点の個数をbとする。すると、
左の図のように横・縦の長さがm・nの長方形の格子点を考える。内部の点の個数をa、周上の点の個数をbとする。すると、
a=(m−1)(n−1)=mn−m−n+1
b=2m+2n
だから、a+(b/2)−1=mn
手順2
 左の図のように横・縦の長さがm・nの長方形の格子点を考える。長方形の内部の点の個数をA、長方形の周上の点の個数をBとする。すると、手順1より、
左の図のように横・縦の長さがm・nの長方形の格子点を考える。長方形の内部の点の個数をA、長方形の周上の点の個数をBとする。すると、手順1より、
A=(m−1)(n−1)=mn−m−n+1
B=2m+2n
次に、対角線を引き直角三角形を考える。mとnの最大公約数が1のとき、この直角三角形の内部の点をa、周上の点の個数をbとすると、
a=A/2=(mn−m−n+1)/2
b=(B/2)+1=m+n+1
だから、
a+(b/2)−1=(mn−m−n+1)/2+(m+n+1)/2−1=mn/2
さて、mとnの最大公約数がgのときは対角線上に(g−1)個の格子点が乗る。(直角を挟む2辺上の点は除く)この直角三角形の内部の点をa、周上の点の個数をbとすると、
a=(A−(g−1))/2=(mn−m−n−g+2)/2
b=(B/2)+1+(g−1)=m+n+g
だから、
a+(b/2)−1=(mn−m−n−g+2)/2+(m+n+g)/2−1=mn/2
手順3
| 内部の点 | 周上の点 | 面積 | |
|---|---|---|---|
| B | a2 | b2 | S2 |
| C | a3 | b3 | S3 |
多角形B、Cが上のようであったとする。すると、
S2=a2+(b2/2)−1 S3=a3+(b3/2)−1
また、多角形B、Cの境界線上の両端を除くところに、p個の格子点があったとすると、 Aについて、内部の点をa、周上の点の個数をbとすると、
a=a2+a3+p
b=b2+b3−2p−2
すると、
a+(b/2)−1
=a2+a3+p+(b2+b3−2p−2)/2−1
=a2+(b2/2)−1+a3+(b3/2)−1
=S2+S3
手順4
| 内部の点 | 周上の点 | 面積 | |
|---|---|---|---|
| A | a | b | S |
| B | a2 | b2 | S2 |
多角形A、Bが上のようであったとする。すると、
S=a+(b/2)−1
S2=a2+(b2/2)−1
また、多角形B、Cの境界線上の両端を除くところに、p個の格子点があったとすると、 Cについて、内部の点をa3、周上の点の個数をb3とすると、
a3=a−a2−p
b3=b−b2+2p+2
すると、
a3+(b3/2)−1
=a−a2−p+(b−b2+2p+2)/2−1
=a+(b/2)−1−(a2+(b3)/2−1)
=S−S2
手順5
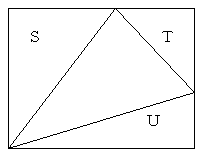 左の長方形はピックの公式が成り立つ。(手順1)
左の長方形はピックの公式が成り立つ。(手順1)
直角三角形Sもピックの公式が成り立つ。(手順2)
手順4より長方形よりSを除いた台形にもピックの公式が成り立つ。
同様にTとUを除いた残りの三角形にもピックの公式が成り立つ。
点順6
一般の多角形は格子点を適当に結んでいけば三角形に分解できる。
すると手順5よりピックの公式が成り立つ。
すると、手順3より、もとの多角形もピックの公式が成り立つ。

| NO.1534 | 2005.4.29. | 佐野允信 | ピックの公式(3) |
(手順1)
長方形ABCDを考える。4頂点A,B,C,Dの座標をそれぞれ(0,k),(0,0),(l,0),(l,k)とする。
ただし、k,lは任意の自然数とする。
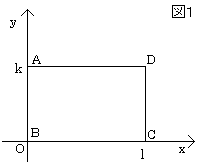
長方形ABCDの内部の格子点の数をa,周上の格子点の数をbとし、長方形ABCDの面積をSとすると、
S=kl ・・・(1)
a=(k-1)(l-1) ・・・(2)
b=2(k-1)+2(l-1)+4=2(k+l) ・・・(3)
(2)(3)より、
a+(1/2)b-1=(k-1)(l-1)+(k+l)-1=kl=S(∵(1)より) ・・・(4)
よって、格子の線上に4辺がある長方形のとき、ピックの公式は成り立つ。
(手順2)
直角三角形BCDと直角三角形ABDを考える。
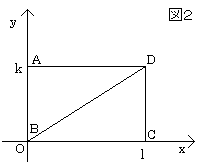
三角形BCDの内部の格子点の数をa1、三角形ABDの内部の格子点の数をa2、
辺BD上の格子点の数をpとする。
対称性より、
a1=a2 ・・・(5)
長方形ABCDの内部の格子点の数はaだから、
a=a1+a2+(p-2)=2a1+p-2(∵(5)より) ・・・(6)
三角形BCDの周上の格子点の数をb1、三角形ABDの周上の格子点の数をb2
とすると、対称性より、
b1=b2 ・・・(7)
長方形ABCDの周上の格子点の数はbだから、
b=(b1-p)+(b2-p)+2=2(b1-p+1)(∵(6)より) ・・・(8)
三角形BCDの面積をS1、三角形ABDの面積をS2とすると、
S1=S2=(1/2)kl ・・・(9)
(6)、(8)より、
| a1+(1/2)b1-1 | =(1/2)(a-p+2)+(1/2){(1/2)b+p-1} |
| =(1/2){a+(1/2)b+1} | |
| =(1/2)S(∵(4)) | |
| =(1/2)kl | |
| =S1 ・・・(10) |
(5)、(7)、(10)より、
| a2+(1/2)b2-1 | =a1+(1/2)b1-1 |
| =(1/2)kl | |
| =S2 ・・・(11) |
したがって、三角形BCDと三角形ABDについて、ピックの公式は成り立つ。 同様にして、直角三角形ABCと直角三角形ACDについても、ピックの公式が成り立つことが示せる。 よって、格子の線上に直角をはさむ2辺がある直角三角形のとき、ピックの公式は成り立つ。
(手順3)
多角形A,B,Cの内部にある格子点の数をそれぞれ、aA,aB,aC,とし、周上にある格子点の数をそれぞれbA,bB,bC
とし、面積をそれぞれSA,SB,SCとする。
SA=SB+SC ・・・(12)
多角形B,Cに対して、ピックの公式が成り立つので、
SB=aB+(1/2)bB-1 ・・・(13)
SC=aC+(1/2)bC-1 ・・・(14)
多角形Bと多角形Cの境界線上にある格子点の数をp1とすると、
aA=aB+aC+p1-2 ・・・(15)
| bA | =(bB-p1)+(bC-p1)+2 |
| =bB+bC-2p1+2 ・・・(16) |
(12),(13),(14),(15),(16)より、
| SA | =(aB-aC)+(1/2)(bB-bC)-2 |
| =(aA-p1+2)+(1/2)(bA+2p1-2)-2 | |
| =aA+(1/2)bA-1 ・・・(16) |
よって、多角形Aに対しても、ピックの公式は成り立つ。
(手順4)
多角形A,Bに対して、ピックの公式が成り立つので、
SA=aA+(1/2)bA-1 ・・・(18)
SB=aB+(1/2)bB-1 ・・・(19)
(15),(16)より、
aC=aA-aB-p1+2 ・・・(20)
bC=bA-bB+2p1-2 ・・・(21)
(12),(18),(19),(20),(21)より、
| SC | =SA-SB |
| =(aA-aB)+(1/2)(bA-bB) | |
| =(aC+p1-2)+(1/2)(bC-2p1+2)) | |
| =aC+(1/2)bC-1 ・・・(16) |
よって、多角形Cに対しても、ピックの公式は成り立つ。
(手順5)
下図のように点A,B,C,D,E,Fをとる。
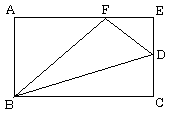
手順1と2より、長方形ABCDと直角三角形ABFに対して、ピックの公式が成り立つので、
手順4より、台形FBCEに対して、ピックの公式が成り立つ。
手順2より、直角三角形FDEに対して、ピックの公式が成り立つので、
手順4より、多角形FBCDに対して、ピックの公式が成り立つ。
手順2より、直角三角形BCDに対して、ピックの公式が成り立つので、
手順4より、三角形BDFに対して、ピックの公式が成り立つ。
従って、格子点上に頂点を持つ一般の三角形に対して、ピックの公式は成り立つ。
(手順6)
格子点を結んでできる一般の多角形を考える。
この多角形は、頂点がすべて格子点上にあるいくつかの
三角形に分割することができる。手順5より、これらの三角形に対して、
ピックの公式が成り立つ。
これらの三角形の中から任意に一つの三角形を選びだし、この三角形をA1とする。
A1に隣接する三角形のうち、任意の一つをA2とする。
手順3より、A1とA2からなる多角形T1に対して、
ピックの公式が成り立つ。
多角形T1に隣接する三角形のうち、
任意の一つをA3とする。
手順3より、T1とA3からなる多角形T2に対して、
ピックの公式が成り立つ。
このように、多角形Tiと、Tiに隣接する任意の三角形Ai+2から
多角形Ti+1をつくると、手順3より、Ti+1に対してピックの公式が成り立つ。
従って、格子点を結んでできる一般の多角形に対して、ピックの公式は成り立つ。
(証明終わり)

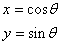
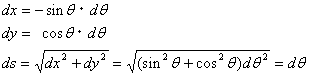
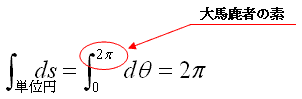 (1)
(1)
 E-mail
E-mail
 戻る
戻る