| NO.1590 | 2006.5.14. | 水の流れ | 3点を通る放物線 |
今回は生徒からの質問です。
点A(1,−2)から放物線 y=x2へ2本の接線を引き、接点をそれぞれB,Cとする。
このとき、3点A,B,Cを通る放物線の方程式を求めよ。できたらエレガントな解答を考えてください。
注:この記事に関する投稿の掲載は、6月12日以降とします。

| NO.1589 | 2006.5.9. | DDT | 展開図は平面になる?(3) |
三角定規様、返答ありがとうございます。だいぶ状況が整理できました。勝手な解釈ですが、以下のように読めました。
(1) 平面に展開できる面は、少なくとも線織面である必要がある。
(2) そのとき投影が、等角かつ等積であれば、等長になる。
(3) そのようなものは、円錐面くらいではないか?
線織面は、Cadでおぼえた言葉ですが、正式な数学用語でもあったと思います。あえて説明しますと、直線エレメントを持った空間曲面です(すいません、やっぱりCad用語でしか喋れません)。
お話を読むまでは、平面に展開可能であれば、等角・等積・等長は当然と考えていたのですが、考えてみれば、任意の曲面の平面への投影は原則常に存在し、それが等積や等長であることはまた別問題です。そうするとまず、平面に展開可能ということを、ちゃんと定義しなくてはと思いました。
ところで、現実の材料(色画用紙)では、それがゴムでもない限り、展開は必ず等角・等積・等長に行われます。そして、等角かつ等積 ⇒ 等長,等角かつ等長 ⇒ 等積 などの関係があると思えます。
結局、投影の像が平面である(曲率0)という拘束条件から、等角,等積,等長の関係が不整合になり、その余りが平面からの高さ(皴)となって現れるのかなと、想像しています。
平面からの高さや曲率が現れるとなると、曲面に張り付いた局所計量の変換を見ているだけでは駄目か?、と一瞬思ったのですが、そうでないという話がガウスの基本形式だと思います。じつはいま、その話の正式な講義を受けている最中なので、講義を聞き終わってから、この問題をもう一度考えてみたいと思っております。
余談ですが、線織面ということで、3次元Cad ⇒ 線織面 の順でInternetを検索したところ、三谷純さんという方の「デジタル時代のペーパークラフト」というHPに当たりました。その目次「7. 展開できる曲面:可展面とは?」には、可展面は線織面の中でも、柱面,錐面,接線曲面に限られるとありました。これらはいずれも、円(円柱,円錐など)でなくても良いと読めます。でもこういう話題って、やっぱり折り紙が発祥の地なのですね。
アドレスは、http://www.j-park.net/~mitani/digital_papercraft/index.htmlです。

| NO.1588 | 2006.5.7. | 三角定規 | 展開図は平面になる?(2) |
確かに習ってはいないですね。
私が幼稚園児童のとき(遠〜〜〜い過去ですが)の記憶です。誕生会のお遊戯で先生が色画用紙をクルクルっと丸め三角帽子(円錐形の帽子)を作ってくれました。
この原体験があったためか,(小学校4・5年だったと思いますが)円錐の展開図を “習った” とき,それが平面に展開できることを何の抵抗も違和感もなく受け入れていました。
(3) 円錐の側面を平面に展開できる理由は?
円錐の “母線” が直線だからでしょう。
曲面は2つのパラメータ (u,v) で表すことができますが,
parametric curve (f(u,v0),g(u,v0),h(u,v0)) が
直線となる身近な曲面は,円柱面 と 円錐面 だけだと思います。
(2) 球の表面も円錐のように北半球だけなら、皴もよらずに平面に展開できるのか?
原点を中心とする半径 a の球面上の点の経度をλ,緯度をδ とすると,
球面は,(acosλcosδ,acosλsinδ,asinδ) と表され,parametric curve λ=λ0(const) も δ=δ0(const) も直線になりません。
だから,半球面は 皴を入れずには平面に展開できない。
(1) 等角かつ等積なら、等長なのか?
Yes! (だと思います。このような変換は,円錐面の展開だけなのではありませんか?)
ここまで書いて思うことは,
空間内で線分の両端を動かすときこの線分が掃いてつくる曲面は,平面に展開可能
なのではないでしょうか。
((やさしく))なくて,申し訳ありません。

| NO.1587 | 2006.5.6. | DDT | 展開図は平面になる? |
全然エレガントじゃないですが、じつは今月の問題112を変分法を用いて解いてみました。過程はどうやら正しそうなのですが、ケアレスミスで不正解となりました。ただ、「卵を砕くのに鉈を持ち出す」ような行為に及んだのには、わけがあります。
正直に言うと、展開することは端から考えていなかったのですが、側面図を展開したとき、それがぴったりと平面の扇型に張り付くのか?という疑問は、昔から持っていました。もちろん解答のやり方は理解できますし、円錐台の側面積を求めるときなどには、似たような考えをいつも用いています。しかし、展開図がぴったり平面に張り付かない空間図形は山ほどあります。例えば、地球儀の表面です。そのために、メルカトル図法(等角図法,四角い世界地図)や等積図法(楕円形の世界地図)など、色々な世界地図があります。
等角図法や等積図法は、角度や面積は保存するものの、距離は嘘になります。今回の解答は、等角かつ等積である投影法のような気がしますが、次のような疑問が生じます。
(1) 等角かつ等積なら、等長なのか?
(2) 球の表面も円錐のように北半球だけなら、皴もよらずに平面に展開できるのか?
(3) 円錐の側面を平面に展開できる理由は?
このようなことは、少なくとも小,中,高では習っていない気がします。どなたか、やさしくご教授くださればと願っています。

| NO.1586 | 2006.5.3. | DDT | 等長変換 |
[等長変換 ⇔ アフィン変換]
以前から、
線形な等長変換 ⇔ 直交変換 (1)
という関係は知っていたのですが、先日、
等長変換 ⇔ アフィン変換 (2)
を示せ、というレポートを出されて、なんだ考えてみればできるじゃないかと気づきました。何をいまさらと仰る人もいるでしょうが、あまり本にも載っていない気がするので投稿いたします。本ではふつう、
アフィン変換 ⇒ 等長変換 (3)
は明らか、という形でしか載っていない気がします。また、(1)もあまり見かけません。ただし、ここで言うアフィン変換は、x∈Rn,ξ∈Rn,
A:Rn→Rn を直交変換として、
f:Rn→Rn が、
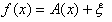 (4)
(4)
となるものをさします。問題を若干正確に述べると、以下となります。
ユークリッド計量を持つRn に、内積から導かれる距離を、x,y∈Rn として、
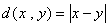
で定義したとき、f:Rn→Rn が、
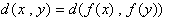
を満たす必要十分条件は、A:Rn→Rn を直交変換,
ξ∈Rn として、
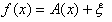
となることを示せ。
(1) A(x)=f(x)−ξは、内積を不変に保つこと
条件より、
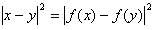
が成り立つ。特に、y=0で考えれば、
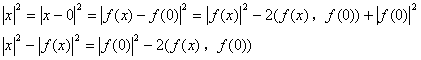 (5)
(5)
となるので、|x−y|2=|f(x)−f(y)|2 より、
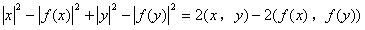
が得られて、(5)を代入すれば、
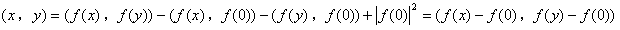
である。よってf(0)=ξとして、A:Rn→Rn を、
A(x)=f(x)−ξで定義した場合、
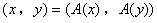
が成り立ち、Aは内積を変えない。
(2) Aが線形であること
Aの表現を求める。そのためにRn の正規直交基底 (ei)i=1〜n
を考えれば、(ei,ej)=δij であるが、Aが内積を変えないことより、(A(ei),A(ej))=δij でもあり、(A(ei))i=1〜n もRn の正規直交基底になる。
(ei) におけるx∈Rn の表現ベクトルを (xi) とすれば、
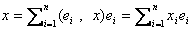
なので、
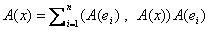
xi=(ei,x)ei
である。同様に、(A(ei)) における A(x)の表現は、
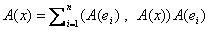
であるが、再びAが内積を変えないことより、
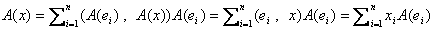 (6)
(6)
が得られる。
(ei) における A(x)の表現が得られれば、それはAの表現になっている
ので、
(ei) における A(x)の表現ベクトルを計算する。それを (xi') とすれば、さっきと同様に、
xi'=(ei,A(x)) なので、(6)を考慮し、
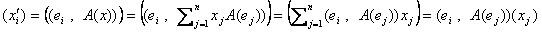
となる。a=((ei,A(ej))) とすれば、aはAの表現行列になっている。
即ちAは、線形でなければならない。
(3) Aが直交変換であること
線形変換Aの表現行列aが、直交行列であることを示す。そのために、次の記法を準備する。
基底 (ei) の各ベクトルを横に並べた横ベクトルを、
B=(ei)=(e1,e2,・・・,en) で表す。名前はどうでもいいんですが、こういうのを超ベクトルというそうですね。というわけで、Bはまだ行列ではありません。同様に、A(B)=(A(ei))=(A(e1),A(e2),・・・,A(en)) とします。この記法と行列記法を併用すると、
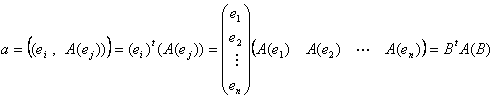
と書けます。最右辺とその前の辺においては、成分をベクトルとした(n行1列) と (1行n列) の(超)行列の、(形式的な)行列積とみなします。この行列積において、成分の積は内積です。この行列積が通常の行列積と同じこと(BやA(B)を行列とみなして良いこと)は、次のように考えればわかります。
問題の条件より、Rn の計量はユークリッド計量なので、その計量テンソルは単位行列Eで定義され、内積に対して、ベクトルとその表現ベクトルを同一視できます。
そこで B=(e1,e2,・・・,en) などの各成分ベクトルei を、その表現ベクトルと同一視し、しかも縦ベクトルとみなせば、
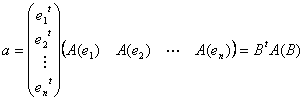
とできるので、これは普通の行列積a=BtA(B) のことです。
このとき、B=(e1,e2,・・・,en) などは、各ei の表現ベクトルei(これは数ベクトル)を、縦ベクトルの形で並べた行列です。
(ei)i=1〜n と (A(ei))i=1〜n が
正規直交基底であることより、BとA(B) は直交行列です(これは当然とします)。従って、
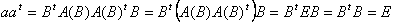
となり、aは直交行列。従って、Aは直交変換。
(4) まとめ
(1)〜(3)で、次のことが導けました。
等長変換で原点を原点に写す ⇒ 内積を変えない変換 ⇒ 内積を変えない線形変換 ⇒ 直交変換
逆に、直交変換 ⇒ 等長変換で原点を原点に写す、は明らかです。従って、
等長変換で原点を原点に写す ⇔ 直交変換
となります。また、
線形等長変換 ⇔ 直交変換
も同時に得られます。もう一つは、線形という条件がなくても、
内積を変えない変換 ⇔ 直交変換
です(まあ、当たり前といえば当たり前なんですが・・・)。
ところで、A(x)=f(x)−ξ(ξ=f(0))でした。よって、f(x)=A(x)+ξ。ここでAは直交変換であり、ξはいわば、その切片。
蛇足ですが、ここまで来ると Rn が任意の計量を持つ場合でも、この一般化はけっこう容易ではないかという気がしてます。多分(3)の超ベクトルと普通の行列との読み替え部分を、計量テンソルを考慮して、任意の計量をユークリッド計量に翻訳するだけでは?、と思いました。

 E-mail
E-mail
 戻る
戻る