Weekend Mathematics/コロキウム室/1998.7〜12/NO.28
コロキウム室
NO.216 12/1 Junko 大相撲本場所(10)
N試合中、3連敗しない(2連敗までは許される)場合の数
をG(N)とします。
具体的にいくつか調べてみます。
- N=1
「○」か「×」 より、G(1)=2
- N=2
「○○」「○×」「×○」「××」より、G(2)=4
- N=3
「○○○」「○○×」「○×○」「×○○」
「○××」「×○×」「××○」より、G(3)=7
- N=4
「○○○○」「○○○×」「○○×○」「○×○○」「×○○○」
「○○××」「○××○」「××○○」「○×○×」「×○×○」
「×○○×」「××○×」「×○××」 より、G(4)=13
ここまで調べて考える・・・。
G(n)+G(n+1)+G(n+2)=G(n+3)
ただし、n≧1という性質を持っているかのかな?
フィボナッチ数列とよく似ていますね。
この漸化式について次のように考えます。

次の3つのケ−スに場合分けできます。
1つは、(N−1)試合目までがどうであれ、N試合目に勝てばいいわけです。
2つめはN試合目に負ける場合ですが、
これは(N−1)試合目が勝った場合にはOKです。
この時、(N−2)試合目までの勝敗は問いません。
更に3つ目は、N試合目に負けて、(N−1)試合目も負けた場合ですが、
これは(N−2)試合目に勝っていればOKです。
というわけで、G(n)+G(n+1)+G(n+2)=G(n+3)
という漸化式が成り立っているというわけです。

NO.217 12/1 水の流れ 大相撲本場所(11)
この数列をトリボナッチ数列といいます。
トリボナッチは人の名前ではありません。
1つの数が前の3つ(トリ)の数の和で得られるので、
フィボナッチ数列の拡張です。

NO.218 12/1 水の流れ パスカルの三角形(1)
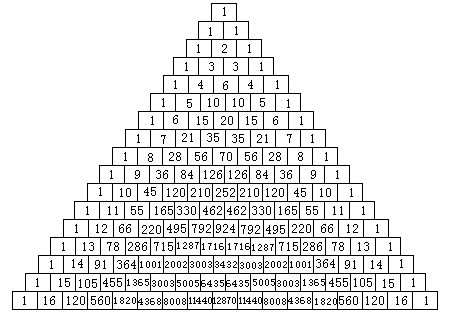
この図を用いて、色分けしてみてください。
例えば、2、3、4、5、6の倍数をすべてぬるというように。
また、nC2もぬってみてください。
他にもいろいろな性質が発見できそう・・・。
(注:図の上で右クリックすると、図(gif画像、8KB)だけを保存、印刷等できます。
Junko)

NO.219 12/2 水の流れ バスケットボ−ルの問題(1)
今、私はバスケットボールの顧問をしています。
競技での得点はフリースローは1点、
フィールドスローは7m以内は2点、
7m以上は3点として加算されていきます。
そこで、試合中スコアブックをみると、
時間と得点経過が示されていました。
問1.10点になるまでの得点経過は何通りですか。
問2.15点になるまでの得点経過は何通りですか。
問3.n点になるまでの得点経過はをT(n)とするとき、
数列T(n)の漸化式はどうなるでしょうか。

NO.220 12/3 Junko バスケットボ−ルの問題(2)
問1.10点になるまでの得点経過を具体的に調べてみました。
1点、2点、3点の得点回数を(x,y,z)で表して、それぞれ何通りかを調べます。
- (10,0,0) → 1
- (8,1,0) → 9C1=9
- (6,2,0) → 8C2=28
- (4,3,0) → 7C3=35
- (2,4,0) → 6C4=15
- (0,5,0) → 5C5=1
- (7,0,1) → 8C1=8
- (5,1,1) → 7C1×7C1=42
- (3,2,1) → 6C1×5C2=60
- (1,3,1) → 5C1×4C1=20
- (4,0,2) → 6C2=15
- (2,1,2) → 5C2×3C1=30
- (0,2,2) → 4C2=6
- (1,0,3) → 4C1=4
以上をすべて足すと、
1+9+28+35+15+1+8+42+60+20+15+30+6+4=274 となります。
問1は10点ですからまだいいとしても、
問2の15点はちょっとやる気がしませんよね。
具体的にやるのはやめて、一般論で考えようと思います。
1点、2点、3点ずつ得点が増えていくというのは、
階段を1段、2段、3段ずつ登っていくのと同じですね。
1段、2段ずつ登るなら、
これはフィボナッチ数列です。
だとしたらこれはトリボナッチ数列かな?
そうです、まさにその通り!
10点に到達するには、次の3通りがあります。
1つは、9点からフリ−スロ−で1点追加し、10点にいたる。
2つ目は、8点から7m以内のフィ−ルドスロ−で2点追加し、10点。
そして3つ目は、7点から7m以上のフィ−ルドスロ−で3点追加し、10点。
というわけです。
つまり、一般的には次の漸化式
T(n−3)+T(n−2)+T(n−1)=T(n) (ただし、n≧4)
が成り立っているというわけです。
T(1)=1、T(2)=2、T(3)=4をこの漸化式に当てはめていくと、
T(4)=7、T(5)=13、T(6)=24、
T(7)=44、T(8)=81、T(9)=149、
T(10)=274となり、先ほどの結果と一致します。
更に、続けます。
T(11)=504、T(12)=927、T(13)=1705、
T(14)=3136、T(15)=5768となります。

NO.221 12/3 水の流れ 駒の動き方(1)
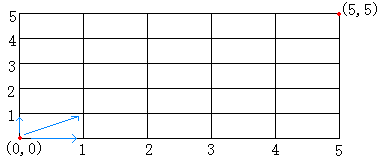
下の図のような碁盤のますの中に、最初一番左下に駒があり、
その座標(0,0)です。
この駒は右、上、斜め上と3通りの方法で1ますづつ動くことができます。
図の一番右上のますの座標(m、n)までたどり着く経路は何とおりですか。
問1.一番右上のますの座標が(5、5)のときの経路は何通りですか。
問2.一番右上のますの座標が(6、4)のときの経路は何通りですか。
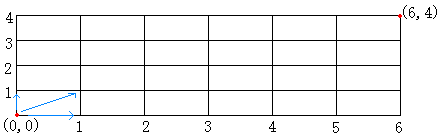
問3.一番右上のますの座標が(m、n)のときの経路は何通りですか。

NO.222 12/4 沖縄の中学3年生 円の証明問題(1)
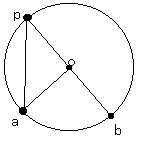 ∠apb=2分の1∠aobであることを証明するには、
どうしたらいいのでしょうか?
∠apb=2分の1∠aobであることを証明するには、
どうしたらいいのでしょうか?

NO.222 12/5 Junko 円の証明問題(2)
こういう風に証明したらどうでしょう。
△opaは二等辺三角形です。なぜなら、op=oa=(円の半径)だからです。
従って、∠opa=∠oapです。
三角形の2角の和は、もう1つの角の外角に等しいという性質がありますから、
∠aob=∠opa+∠oap=2∠opa
このことから、同じ弧に立つ円周角は中心角の半分であるということが証明できたというわけです。

 E-mail
E-mail
 戻る
戻る


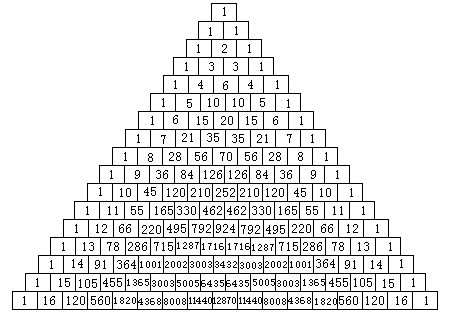


 ∠apb=2分の1∠aobであることを証明するには、
どうしたらいいのでしょうか?
∠apb=2分の1∠aobであることを証明するには、
どうしたらいいのでしょうか?
 E-mail
E-mail
 戻る
戻る