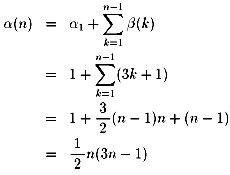
Weekend Mathematics/コロキウム室/1999.7〜9/NO.68
| NO.586 | '99 7/20 | Junko | オイラーの「無限解析入門(1)」(27) |
α(1)=1,α(2)=5,α(3)=12,α(4)=22,・・・の一般項を求めてみます。
この数列の階差数列(隣同士の差をとって作った数列)をβ(n)とします。
β(1)=4,β(2)=7,β(3)=10,・・・となり、
これは初項4、公差3の等差数列になっています。
従ってβ(n)=4+3(n−1)=3n+1
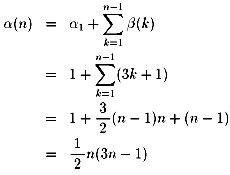

| NO.587 | '99 7/20 | Junko | 相加平均と相乗平均(2) |
a0>0、b0>0、a0≠b0と考えます。
a0、b0の大小関係はさておき、
相加平均≧相乗平均の関係(等号成立は2者が等しいときのみ)から、b1<a1
b2、a2はこれらの相加平均と相乗平均ですから、
b1<b2<a2<a1
以下同様に、b1<b2<b3<a3<a2<a1
・・・
これより、数列{an}は単調減少、かつ下に有界
(任意のnに対して、b1<an)
数列{bn}は単調増加、かつ上に有界
(任意のnに対して、bn<a1)
従って、数列{an}、{bn}はともに収束する。
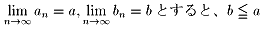
b=aを証明するために背理法を使います。つまり、b<aと仮定します。
数列{an}は単調減少なので任意のnについて、a<an
数列{bn}は単調増加なので任意のnについて、bn<b
ここでb<aより、a−b=εとする。
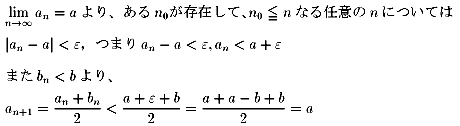
これは任意のnについて、a<anであることに矛盾します。
従って、a=bというわけです。
イメ−ジとしては、a0、b0からスタ−トして
相加平均と相乗平均をとっていくわけですから、両者に溝ができるはずはない(つまり一致する?)といった感じでしょうか。
この数列の収束は早そうですね。

| NO.588 | '99 7/20 | 水の流れ | オイラーの「無限解析入門(1)」(28) |
オイラーの無限解析入門(1)の第14夜の始まり、始まり。
皆さんは、次の数列の名前をご存じでしょう。
三角数 1,3,6,10,15,21,28、36、・・・
四角数 1,4,9,16,25,36,・・・
五角数 1,5,12,22,35,51,・・・
13夜の数列がこの五角数なのです。
さて、歴史的なことを書きます。
1740年にフランス系のベルリンの数学者ノデがオイラーに手紙を書いて、
与えられた整数nが幾通りの方法でk個の異なる整数の和として表されるかを問うて来た。
(ここで、扱っている記号ではA(n)のことです。)
オイラーは直ちにといっていいくらいに返事をした。
次いで、2,3ヶ月もせぬうちに、ペテルスブルク・アカデミーに論文を提出した。
彼は後に数度にわたりこの問題に立ち戻ることになった。
1748年の「無限解析入門(1)」にいくらか詳しく、この問題を扱っており、
また最後に扱ったのは1768年のことであった。
ノデの問題に対するキーは次の無限積が無限級数へ展開されることが彼の心を打ったのは
言うもでもない。
零でない係数がどれも±1であるということばかりでなく、
指数が容易に分かるように「五角数」n(3n−1)/2である。
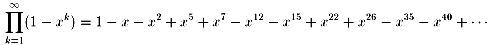
(これが、オイラーの五角数定理、または、オイラーの恒等式という。)
1750年、オイラーはほぼ10年を要して、この証明をゴールドバッハに送ることができた。
ヤコービが見いだしたように、正確な証明はテータ関数や保型形式の理論を待たねばならない。
<以上までの参考文献:数論(アンドレ・ヴェイユ;足立恒雄訳)「日本評論社」>
また、この公式のことを数学セミナー3月号の載っている静岡大学の浅井哲也先生は
「数論に現れるいくつかの不思議な等式に魅力を引かれるようになりました。
僕にとっての数学の女神さまは、多少象徴的な言い方になりますが、例えば、この五角数定理でした。」
とね。
これで、本題にもどります。
| f(x) | =(1+x+x2+x3+x4+x5+x6+x7+x8+x9+x10+・・・) |
| (1+x2+x4+x6+x8+x10+・・・) (1+x3+x6+x9+・・・) | |
| (1+x4+x8+・・・) (1+x5+x10+・・・) (1+x6+・・・) | |
| (1+x7+・・・) (1+x8+・・・) (1+x9+・・・) (1+x10+・・・) | |
| =s(0)+s(1)x+s(2)x2+・・・+s(m)xm+・・・・ |
ここで、今夜の宿題です。
左辺のxmの係数は0に等しいですから、
ここから、s(m)を求める関係式を発見してください。
今夜は長くなりましたが、徐々にオイラーの域に近づくことができました。
みなさん、お休みなさい。

| NO.589 | '99 7/24 | 月の光 | 相加平均と相乗平均(3) |
問題に出てきたカール君というのはあの天才数学者カール・フリードリヒ・ガウスのことです。
14歳のときガウスはこの数列を計算し、双方の数列がただちに同じ極限M(a0,b0)に収束する事を
発見しました。
これは算術幾何平均とよばれました。
当時ガウスは、2定点A,B(焦点)からの距離の積が一定で
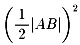 に等しい点の軌跡であるレムニスケートとして
知られていた曲線に興味を持ち、長い間その弧張を発見しようと努め、
に等しい点の軌跡であるレムニスケートとして
知られていた曲線に興味を持ち、長い間その弧張を発見しようと努め、
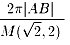 と推定しました。
最初証明ぬきで11桁(!)まで双方の量を計算したそうです。
と推定しました。
最初証明ぬきで11桁(!)まで双方の量を計算したそうです。
<参考文献:ガウスが切り開いた道(シュプリンガー・フェアラーク東京)>

| NO.590 | '99 7/26 | 水の流れ | 緊急連絡網(1) |
太郎さんの学校では、9月1日の「防災の日」までに、
災害時のとき、生徒の
安全確認用緊急連絡網を作成して、提出する課題があります。
電話を通して(不通の場合は、全員持っている携帯電話を使用)
クラスの生徒(n―1)人の安全確認を担任の太郎さんを含めて、
お互いに情報を流し合います。
例えば、担任と生徒Aさんの間の1回の電話で、
担任の太郎さんは自分が聞いた、すべての生徒の安否を生徒に伝え、
生徒Aさんも自分が聞いた安否を担任に伝えます。
もちろん、生徒同士でも当然お互いの安否を伝え合います。
太郎さんを含めて、n人の人々の間で、
すべての安全確認に必要な最少通話回数をS(n)で表すとき、
次の問題に答えてください。
問題1:
電話連絡の順序を書いて、S(2)、S(3)、S(4)
を求めてください。
問題2:
太郎さんと生徒9人の場合で、通話回数が16回で、安否確認が10人
すべてにいきわたる連絡網(順序つき)を1つ作成してください。
問題3:
一般に、生徒3人以上に対して、S(n)≦2n―4を示してください。

| NO.591 | '99 7/26 | Junko | それいけ算数! |
今日からNHK教育テレビの11:00〜11:15で、「それいけ算数」という番組が始まりました。
8/6(金)までの10回シリ−ズで、小学生向けに実験や工作を織り交ぜて、
算数のおもしろさを体験できるようです。
小学生向けとはいってもなかなか奥が深く、おもしろそうです。
講師は秋山仁さんです。
テキストは本屋さんで売っています。(\900切り抜き付録つき)
第1回目のテ−マは「チョコ・ケ−キの3等分」でした。
これは、NO.232 クリスマスケ−キの問題として
以前コロキウム室でも取りあげた内容です。

| NO.592 | '99 7/27 | Junko | 緊急連絡網(2) |
問題1について、具体的にやってみます。
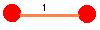
| S(2)=1 |
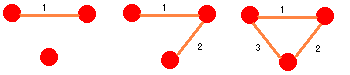
| S(3)=3 |
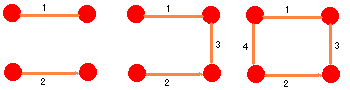
| S(4)=4 |

| NO.593 | '99 7/28 | Junko | 緊急連絡網(3) |
問題2について
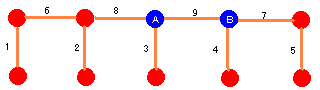
上の図のように、順番に連絡を取り合っていきます。
ひととおり、連絡が取り終わった段階で、青い人物A,Bの2人はすべての人の情報を
持っています。
ここまでは、どういう形態をとろうとも9(=10−1)とおりです。
それはチ−ム数Nとしたときの、ト−ナメント試合の数がN−1になるのと同じ理由です。
(NO.573)
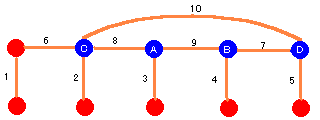
次にCに着目すると、CはAから左の情報をすべて持っています。
同様に、DはBから右の情報をすべて持っています。
そこでCとDが連絡を取り合えば、CとDはすべての情報を得ることができます。
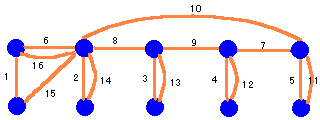
次にすべての情報をすべて持っている人物(青で表示されたA,B,C,D)が、 残った人たちに連絡を取っていけば,16回の連絡で完了です。
問題3について
一般にn人で連絡を取り合う時も同様に考えます。
まず、順にひととおり情報収集をします。
この段階で2人の人物A,Bがすべての人の情報を得ることになります。
ここまでで(n−1)回。
次にA,Bが連絡を取り合う前の段階で、Aと同じ情報量のC、Bと同じ情報量のDという人物がいるはずです。
この2人が連絡を取り合うことで、彼らもすべての情報を得ることになります。
最後にA,B,C,Dを除く人物に連絡を取っていきます。
これが(n−4)回。
従って、(n−1)+1+(n−4)=(2n−4)回。
でも、nが増えた時にはもっと効率的な方法がありそうですから、
ここは謙虚に不等号にしましょう。
つまり、S(n)≦2n−4、ただしn≧4かな?

| NO.594 | '99 7/29 | Junko | ト−ナメント戦(4) |
高校野球夏の大会、神奈川地区大会は今日決勝戦が行われ、桐蔭学園が優勝しました。
205校で争ったこの神奈川県大会、優勝するには連続何試合に勝たねばならないのでしょうか?
128<205<256 つまり、
27<205<28ということですから7ないし8試合ということになります。
シ−ド校やくじ運よく第1試合のないチ−ムは7試合、くじ運の悪いチ−ムは8試合もこなさなければなりません。

 E-mail
E-mail
 戻る
戻る