
Weekend Mathematics/コロキウム室/テーマ別
/15.ゼーター関数物語1
NO.336 '99 2/15 水の流れ ゼーター関数物語(1)
「数学の知性」W.ダンハム著:中村由子訳(現代数学社)
読んで、これからゼター関数ζ(2)物語を投稿します。
「時は、17世紀後半ヨーロッパ大陸のフランスのパリにドイツの外交官
として、派遣されていたライプニッツ(1646〜1716)がいました。
幸運なことに、当時ドイツの科学者ホイエンス(1629〜1695)は
パリに在住していました。このホイエンスに数学の勉強を教わっていました。
さて、このときの問題です。
みなさんは三角数をご存じですか?1,3,6,10,・・・
と三角形になるように配置したときの数字です。
では、その三角数の逆数の和を求めてください。
すなわち、S=1+1/3+1/6+1/10+・・・・
のSの値を求めてください。」
<注: 実は、この解法がライプニッツのパリ在住4年間(1672〜1676)
の数学的洞察力を開花させるきっかけとなったものです。>

NO.338 '99 2/16 みや ゼーター関数物語(2)


NO.339 '99 2/16 水の流れ ゼーター関数物語(3)
ゼター関数ζ(2)物語を第2夜を送ります。
「17世紀後半、1684年、ライプニッツは学術誌
「Acta Eruditorum]に
素晴らしき微分学を発表しました。
ライプニッツは1716年亡くなりましたが、
この後継者である二人のスイス人の兄弟はヨーロッパ中に微分を広め、
定着させる大きな力になりました。
兄ヤコブ・ベルヌーイ(1654〜1705)は確率論で知られています。
弟ヨハン・ベルヌーイ(1667〜1748)は兄ヤコブが1689年
発表した「無限級数に関する論文」の中に
”調和級数は無限大に発散する”ことを証明しています。
ここで、問題です。
調和級数 1+1/2+1/3+1/4+1/5+・・・・・は無限大に発散する。
皆さんは、これを現代風にでも結構ですので、証明してください。
後で、ヤコブ著「tractatus」(1713年)
の中での発散の証明を書きます。今日はここまです。

NO.343 '99 2/18 Junko ゼーター関数物語(4)


NO.344 '99 2/19 水の流れ ゼーター関数物語(5)
「ゼター関数ζ(2)物語第3夜の始まり、始まり。
見事に、調和数列 1+1/2+1/3+1/4+1/5+・・・
が無限大に発散する証明が終わりました。
ところが、弟ヨハン・ベルヌーイは兄ヤコブ著「tractatus」の中で、
ライプニッツの収束する級数
1/2+1/6+1/12+1/20+・・・=1
を利用して、こんな風に書いています。
<証明> 最初の項を省いて、調和数列を
A=1/2+1/3+1/4+1/5+・・・ とおく。
さらに、後に参照するために、分子が1,2,3,4,・・・
となるよう変換しておきます。
すると、
A=1/2+2/6+3/12+4/20+5/30+・・・
ライプニッツの収束する級数をCとおき、それから順次
1/2、1/6、1/12、1/20、・・・
を省きながら一連の級数を作ります。
C=1/2+1/6+1/12+1/20+1/30+・・・=1
D=1/6+1/12+1/20+1/30+・・・=C−1/2=1/2
E=1/12+1/20+1/30+・・・=D−1/6=1/2−1/6=1/3
F=1/20+1/30+・・・=E−1/12=1/3−1/12=1/4
G=1/30+・・・=F−1/20=1/4−1/20=1/5
・・・
ここで、ヨハンは上の整然と並んだ式の式を左から順に縦に足してみます。
すると
C+D+E+F+G+・・・ =1/2+(1/6+1/6)+(1/12+1/12+1/12)+ (1/20+1/20+1/20+1/20)+・・・ =1/2+2/6+3/12+4/20+・・・ =A皆さん、何か気がつきましたか。 先にあげた式とまったく同じものになっています。
C+D+E+F+G+・・・=1+1/2+1/3+1/4+1/5+・・・ =1+Aであることがわかります。

NO.346 '99 2/19 みや ゼーター関数物語(6)
調和級数が発散することの証明です。
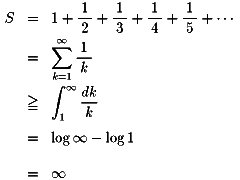
この証明はあっているかどうか自信はありません。
シグマから積分に変形しているあたりが怪しいです。

NO.348 '99 2/20 Junko ゼーター関数物語(7)

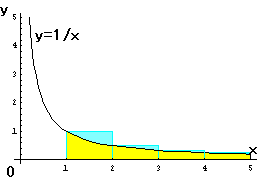

NO.350 '99 2/21 Junko ゼーター関数物語(8)
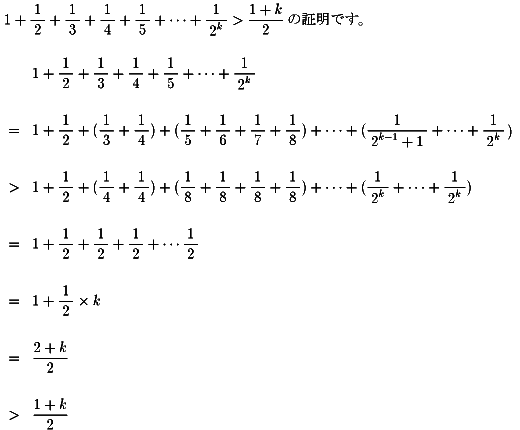

NO.351 '99 2/21 水の流れ ゼーター関数物語(9)
「ゼーター関数ζ(2)物語第4夜の始まり、始まり。
昨夜、こんな問題を出したままでしたね。
『任意の整数をkとして、
1+1/2+1/3+1/4+・・・+1/2k>(k+1)/2』
皆さん、ニコル・オレスムと同じ証明になるでしょうか?
もし、そうなら数学的真理の普遍性を実感します。
実は、ニコル・オレスムの証明と同じことが、6世紀後でも、
「Junko」さんが
NO.343で証明しています。
数学的真理の神秘に驚いています。
さて、ヨハン・ベルヌーイはもう1人の数学者イタリアの
ピエトロ・メンゴーリにも先を越されています。
メンゴーリの証明は1647年、ベルヌーイの証明の40年
ほど先立つものでした。
これは実にシンプルな証明ですが、まず最初に前提になる定理が出てきます。
第4夜の問題です。皆さん、解いてみてください。
『任意の整数をkとして、
1/(k−1)+1/k+1/(k+1)+>3/k である』
この定理は3個の連続する整数の逆数を足したとき、
その和は真ん中の数の逆数の3倍より大きいという問題です。
これが、メンゴーリが1647年に行った短い証明の
中で調和級数への挑戦に必要な定理でした。」

NO.355 '99 2/22 みや ゼーター関数物語(10)
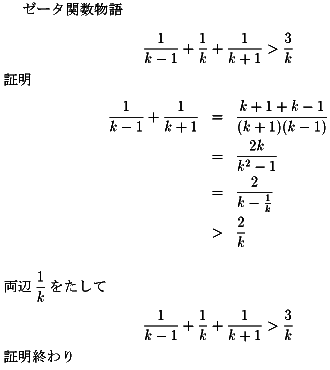

NO.356 '99 2/22 Junko ゼーター関数物語(11)


NO.357 '99 2/23 水の流れ ゼーター関数物語(12)
「ゼーター関数ζ(2)物語第5夜の始まり、始まり。
さて、前提になる定理も無事証明出来ました。
ここで、1647年に行ったメンゴーリの証明を紹介します。
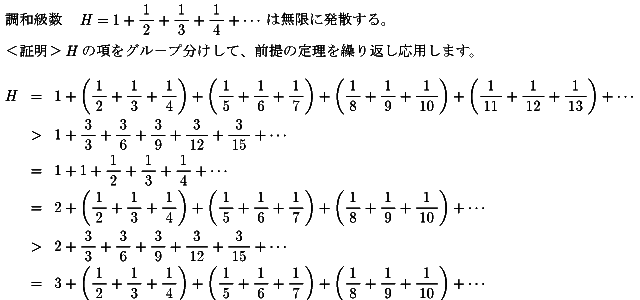
といった具合に続いていきます。
メンゴーリの論証の美しさは自己複製していくところにあります。
ステップごとに先行条件の定理を適用し、
新たに同じような調和数列に出会うことになりますが、
そのときは1増えているというわけです。
上に揚げた不等式を見ると、Hは1より大きく、
2より大きく、3より大きくなっていて、
実際にこの手順を繰り返していkrば、たとえどんな有限数を
設定してもHはそれをしのぐ数であることが分かります。
そういうわけで、ヨハンの偉大なる定理は証明方法は異なるにしてもオレスム、
メンゴーリの後塵を拝していたわけです。
さて、【数学の知性】という本から離れますが、
よく見かける次の無限級数の値を覚えていても有意義なことです。
『次の無限級数の値を証明してみてください。
<今夜の問題ではありませんが>
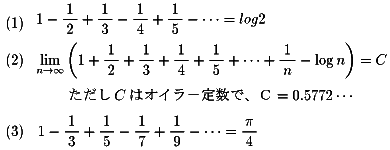
それでは、物語にもどります。
ヤコブはまた「tractatus」において、
この調和級数を前提に
整数を2乗したものの逆数の和にも触れています。すなわち、
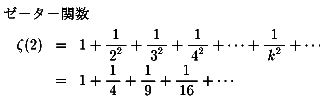
では、今夜の問題です。
ヤコブはこの級数が2より小さいことは分かっていました。
『 1+1/4+1/9+1/16+・・・<2 を証明しましょう。』
この値は1734年、他でもないヨハン・ベルヌーイのもとで数学を学んだ一人の
若者によって解決されることになります。
この続きは、明日の夜お話しましょう。お楽しみに! 」 終わり

NO.361 '99 2/24 Junko ゼーター関数物語(13)

NO.363 '99 2/24 月の光 ゼーター関数物語(14)
NO.357の(1)(3)の証明です。
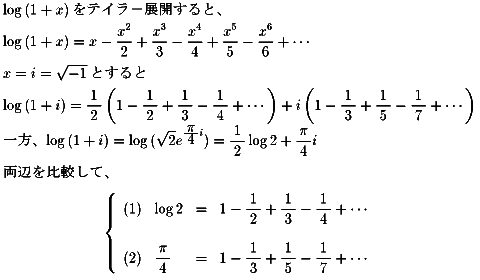

NO.364 '99 2/24 Junko ゼーター関数物語(15)
NO.357の(1)だけなら、
NO.363におけるlog(1+x)のテイラ−展開において、
x=1を代入することで得ることができますね。

NO.365 '99 2/24 みや ゼーター関数物語(16)


NO.367 '99 2/25 月の光 ゼーター関数物語(17)


NO.368 '99 2/25 水の流れ ゼーター関数物語(18)
「ゼーター関数ζ(2)物語第6夜の始まり、始まり。
昨晩、こんな証明を出しましたね。皆さんは容易に証明できましたね。
『 1+1/4+1/9+1/16+・・・<2 を証明しましょう。』
この結果、一般に数列a(n)について、単調増加で上に有界な数列は
収束しますから、ヤコブは何らかの有限な数に収束することを示しましたが、
ベルヌーイ兄弟にはその和の正確な値を出すことはできませんでした。
ヤコブは”今もって私たちの必死の探求の目をかいくぐっている、
その答えを教えてくれる人があるならば、私たちは多いに感謝する・・・”
と言い訳をしています。
ベルヌーイ兄弟は何もアイデアももっていませんでした。
それどころか、かのライプニッツ
その人さえ明らかに手に負えない問題だったのです。
この級数、1+1/4+1/9+1/16+・・・の正確な和を求める問題は大変
難解で、捕まえどころのない数値を出すためにはベルヌーイ兄弟以上の
天才的能力が必要でした。
面白いことに、この問題は1734年、他でもないヨハン・ベルヌーイのもとで
数学を学んだ一人の若者によって解決されました。
その生徒こそ、偉大なるレオンハルト・オイラーその人でした。
この驚異的な人物は1707年、スイスのバーゼルに生まれました。
当然ながら、幼いときからのその天才ぶりを発揮し、
牧師である父親は息子をあの高名なヨハン・ベル
ヌーイのもとで学べるように奔走したのでした。
1727年、オイラーはロシアのセントペテルスブルグ大学に
医学と生理学のポストに就きました。
その後、1733年、ついにオイラー
にも数学教授の椅子が巡ってきました。
不幸なことに1730年代の中頃から右目の視力が
落ち始め、まもなくまったくみえなくなってしましました。
オイラーがセントペテルスブルグ大学での初年度、
1734年に発表したのがゼーター関数
ζ(2)=1+1/4+1/9+1/16+・・・の値でした。
このとき、彼はこう語っています。
”・・・私は予想もしなかったエレガントな式を発見した。
・・・それもπを用いてのものである。
オイラーの偉大なところは同じ式を2種類の方法で表現して、
結びつけるところにあります。
どこまでも異なる2つの見地から1つの目標を見出していく能力が、
彼の最も深遠で美しい論証を特徴づけています。
さて、ここで、第6夜の問題です。
手始めに、次の無限級数と無限積が等しいことを証明する必要があります。
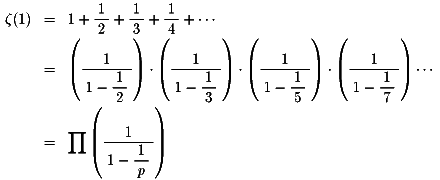
ただし、右辺はすべての素数pにわたる無限積を表します。
この感覚をつけておかないと、随所にでてきます。
今夜はこれで終わりです。ちなみに、上のことが分かった人はNO.359の
「素数の逆数の総和」の証明は容易にできるでしょう。

NO.369 '99 2/25 みや ゼーター関数物語(19)


NO.373 '99 3/1 Junko ゼーター関数物語(20)
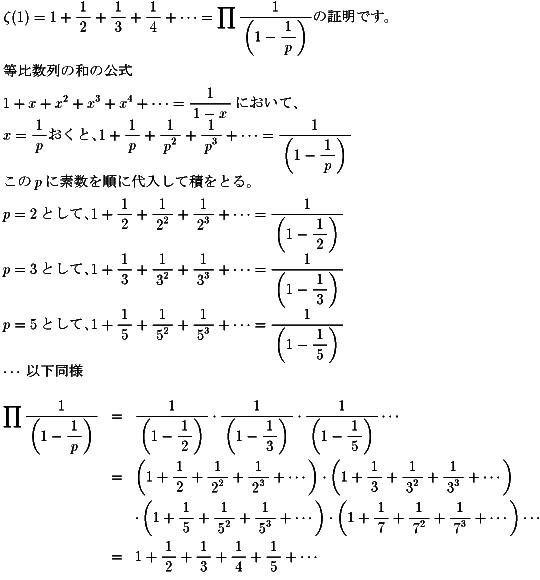

 戻る
戻る