Weekend Mathematics/コロキウム室/1999.1〜3/NO.43
コロキウム室
NO.357 '99 2/23 水の流れ ゼーター関数物語(12)
「ゼーター関数ζ(2)物語第5夜の始まり、始まり。
さて、前提になる定理も無事証明出来ました。
ここで、1647年に行ったメンゴーリの証明を紹介します。
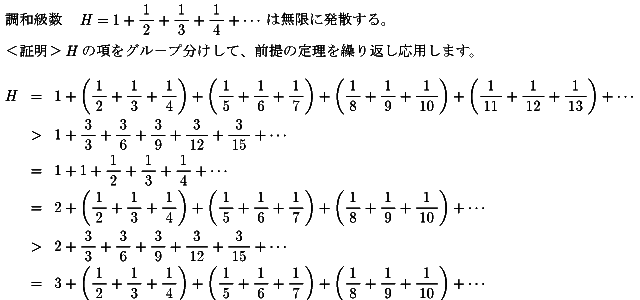
といった具合に続いていきます。
メンゴーリの論証の美しさは自己複製していくところにあります。
ステップごとに先行条件の定理を適用し、
新たに同じような調和数列に出会うことになりますが、
そのときは1増えているというわけです。
上に揚げた不等式を見ると、Hは1より大きく、
2より大きく、3より大きくなっていて、
実際にこの手順を繰り返していkrば、たとえどんな有限数を
設定してもHはそれをしのぐ数であることが分かります。
そういうわけで、ヨハンの偉大なる定理は証明方法は異なるにしてもオレスム、
メンゴーリの後塵を拝していたわけです。
さて、【数学の知性】という本から離れますが、
よく見かける次の無限級数の値を覚えていても有意義なことです。
『次の無限級数の値を証明してみてください。
<今夜の問題ではありませんが>
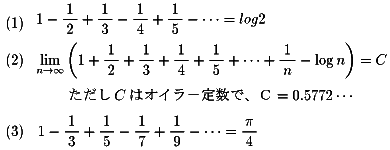
それでは、物語にもどります。
ヤコブはまた「tractatus」において、
この調和級数を前提に
整数を2乗したものの逆数の和にも触れています。すなわち、
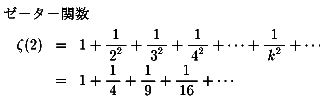
では、今夜の問題です。
ヤコブはこの級数が2より小さいことは分かっていました。
『 1+1/4+1/9+1/16+・・・<2 を証明しましょう。』
この値は1734年、他でもないヨハン・ベルヌーイのもとで数学を学んだ一人の
若者によって解決されることになります。
この続きは、明日の夜お話しましょう。お楽しみに! 」 終わり

NO.358 '99 2/23 月の光 1999!の桁数(7)


NO.359 '99 2/23 月の光 素数の逆数の総和
調和級数が発散する事は示されましたが、
素数の逆数の総和はどうでしょうか?
素数が無限に存在する事をまず示してから考えてみて下さい。

NO.360 '99 2/23 Junko 2000年問題?(3)

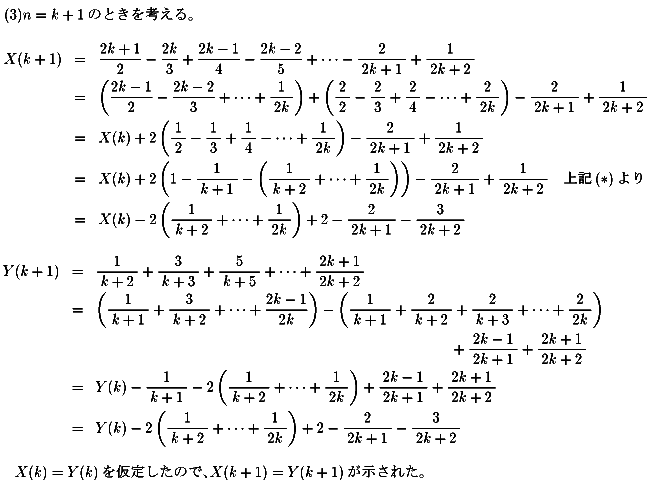

NO.361 '99 2/24 Junko ゼーター関数物語(13)
NO.357
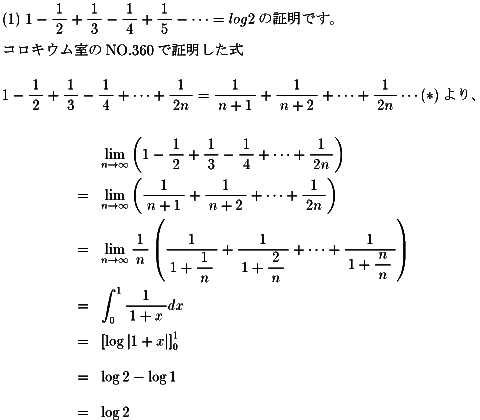

NO.362 '99 2/24 Junko 正四面体の問題
16日に実施された神奈川県立高校の入学試験に出された問題です。
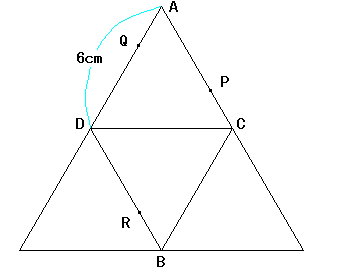 右の図は、1辺の長さが6cmの正四面体ABCDの展開図である。
右の図は、1辺の長さが6cmの正四面体ABCDの展開図である。
3点、P,Q,Rは、それぞれ正四面体の辺AC,DA,DB上の点であり、
AP:PC=DQ:QA=DR:RB=2:1である。
このとき、この展開図からつくられる正四面体について、
次の問いに答えなさい。
(ア)この正四面体ABCDにおいて、2点A,R間の距離を求めなさい。
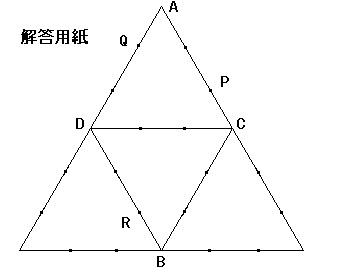 (イ)3点P,Q,Rを通る平面でこの正四面体ABCDを切り、
2つの立体に分けるとき、切り口の図形のすべての辺を、
解答用紙にある展開図に書き入れなさい。
ただし、解答用紙にある展開図の辺上の印「・」は、
それぞれの辺を3等分する点を示している。
(イ)3点P,Q,Rを通る平面でこの正四面体ABCDを切り、
2つの立体に分けるとき、切り口の図形のすべての辺を、
解答用紙にある展開図に書き入れなさい。
ただし、解答用紙にある展開図の辺上の印「・」は、
それぞれの辺を3等分する点を示している。

NO.363 '99 2/24 月の光 ゼーター関数物語(14)
NO.357の(1)(3)の証明です。
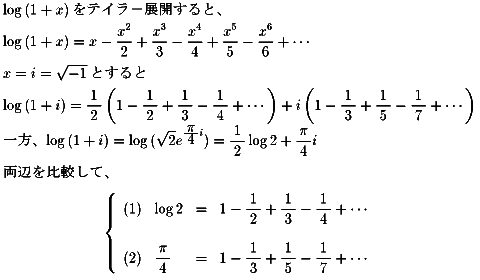

NO.364 '99 2/24 Junko ゼーター関数物語(15)
NO.357の(1)だけなら、
NO.363におけるlog(1+x)のテイラ−展開において、
x=1を代入することで得ることができますね。

NO.365 '99 2/24 みや ゼーター関数物語(16)


 E-mail
E-mail
 戻る
戻る
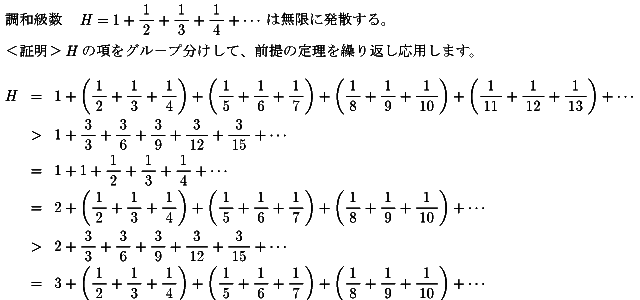
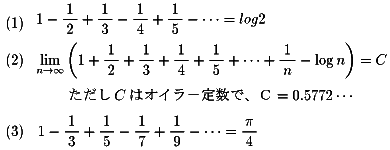
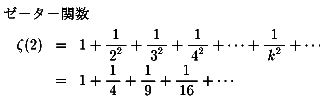



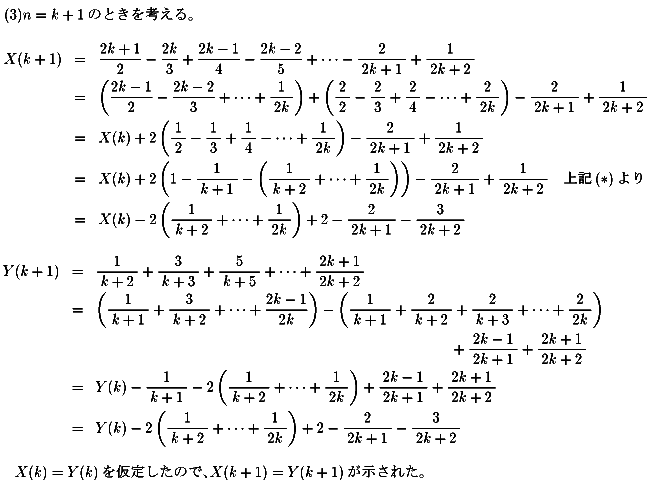
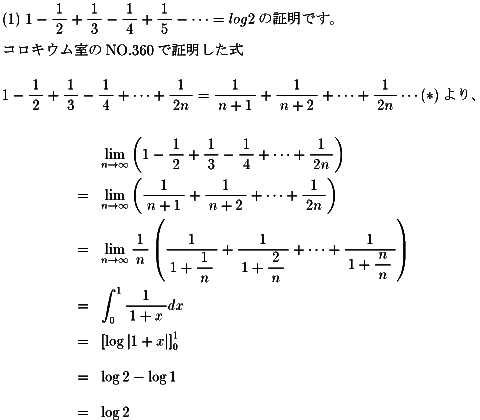
 右の図は、1辺の長さが6cmの正四面体ABCDの展開図である。
右の図は、1辺の長さが6cmの正四面体ABCDの展開図である。 (イ)3点P,Q,Rを通る平面でこの正四面体ABCDを切り、
2つの立体に分けるとき、切り口の図形のすべての辺を、
解答用紙にある展開図に書き入れなさい。
ただし、解答用紙にある展開図の辺上の印「・」は、
それぞれの辺を3等分する点を示している。
(イ)3点P,Q,Rを通る平面でこの正四面体ABCDを切り、
2つの立体に分けるとき、切り口の図形のすべての辺を、
解答用紙にある展開図に書き入れなさい。
ただし、解答用紙にある展開図の辺上の印「・」は、
それぞれの辺を3等分する点を示している。
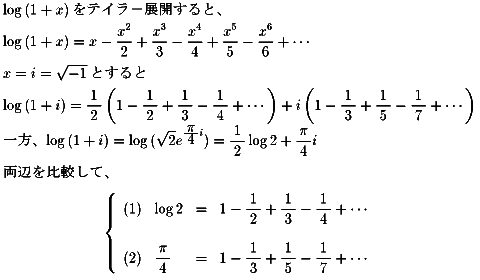

 E-mail
E-mail
 戻る
戻る