Weekend Mathematics／問題／問題47
４７．行きつ戻りつの問題
１．
水面まで深さ２０ｍの井戸がある。 今、カタツムリが外へ出ようと水面から歩き始めた。 しかし、昼間は８ｍ進めるが、夜は寝るため、４ｍ下がってしまう。 さて結局、何日で出られるのでしょうか？
２．
あきらくん(時速４ｋｍ)と愛犬ポチ(時速１０ｋｍ)は２ｋｍ先にあるわが家をめざしてスタートした。 当然のごとく、ポチが先に家についたが、そこは名犬（？）。 ポチは家につくなりすぐ引き返し、まだ歩いているあきらくんのところに 戻って、また家にいくことを繰り返した。 さて、結局あきらくんが家につくまで、ポチは何ｋｍ走ったことになるのでしょう？
頭のよくなる本
ピ−タ−フランクル
WAVE出版
答えと解説
（ペンネ−ム：佐々木一樹）
１日目０→８→４ ２日目４→１２→８ ３日目８→１６→１２ ４日目１２→２０
ということで、答えは４日
（ペンネ−ム：kumapu）
20÷(８−４)＝５で、5日…と考えがちですが、(笑)
四日ですネ。
何故なら、４日目、に上りきってしまって、落ちないから…？でいいのかな。
（ペンネ−ム：細井 夏樹）
１日に進む距離は ８−４＝４ｍ
但し、最終日は寝る前に井戸の外へ出られるため、８ｍ進むことができる。
以上より、 ４×(α−１)＋８＝２０ ：α＝日数
これを解いて、 α＝４ 答、４日
（ペンネ−ム：teppei）
answer is fourth, because we can't count fourth night.
（ペンネ−ム：Oitan）
Answer: 4 days (more specifically , at the end of day time on the fourth day)
A simple question like this usually indicates hidden traps.
Simple calculation will lead to an answer of 5 days, but actually it is too
straightforward.
By checking how far the snail can proceed for each day time/ night time,
we will get 4 days.
1st day day time 8
night time 4 (=8-4)
2nd day day time 12 (=4+8)
night time 8 (=12-4)
3rd day day time 16(=8+8)
night time 12 (=16-4)
4th day day time 20 (=12+8) Here we go!
（ペンネ−ム：Kohda）
結局一日４ｍのぼるから２０÷４で五日かかると思いきや三日で１２ｍのぼった
あと四日目の昼間に到着します。と言うわけで答えは四日
（ペンネ−ム：ＳＨＯ）
１日あたり差し引き4ずつ進んでいるので5日、
といいたいところだが４日目の朝に１２メートルなので
４日目の終わりに２０メートルに到達する。
答.４日
（ペンネ−ム：KOSUGI）
１日に登ることが出来る距離は（８−４）＝４メートルなので、
３日目終了時点で１２メートル登ることになる。
ところが、４日目の昼間に残りの８メートルを上り切ってしまう。よって答は４日目の昼間。
（ペンネ−ム：kiyo）
（８−４）＋（８−４）＋（８−４）＋８＝２０（ｍ）
答え ４日。
（ペンネ−ム：かつ）
深さ20メートルの井戸からカタツムリが井戸から出るまでの問題です
昼間は８ｍ進み、夜は４ｍ後退するので・・・。
結局１日４ｍ進むことになります。
よって
２０÷４＝５で５日と言いたいところですが、そうではないですね。
ここで３日目の夜が過ぎ４日目の朝がきたときには、残り８ｍのところに来ています。
つまり４日目に昼間８ｍ進むと地上についてしまうのです。
夜にわざわざ４ｍ下がることは無いので、答えは４日になります。
１日４メートル進むと言うことにしてしまうと間違ってしまうのです。
そこさえ気がつけば、問題なく解けると思います。
（ペンネ−ム：夜ふかしのつらいおじさん ）
４日で出られます。
次ぎの図から明らかでしょう。（矢印１つは１ｍ分）
２０ ↑・・・・・・・・４日目の到着地点【井戸の出口】 １９ ↑ １８ ↑ １７ ↑ １６ ↑↓↑・・・・・・・・３日目の到着地点 １５ ↑↓↑ １４ ↑↓↑ １３ ↑↓↑ １２ ↑↓↑・・・・・・・・・・・・２日目の到着地点（４日目の出発地点） １１ ↑↓↑ １０ ↑↓↑ ９ ↑↓↑ ８ ↑↓↑・・・・・・・・・・・・・・・・１日目の到着地点（３日目の出発地点） ７ ↑↓↑ ６ ↑↓↑ ５ ↑↓↑ ４ ↑ （２日目の出発地点） ３ ↑ ２ ↑ １ ↑ （１日目の出発地点）【水面】
（ペンネ−ム：高橋 道広 ）
まず最初の問題は
２０/4=5ではだめなんですね。
２０−８＝１２ 12/4=3で、3日であと８ｍを残すことになります。そして4日にめでたく8Mを進み
外に出る…と思うでしょ
しか〜し、4日目には、８ｍ進んで、井戸の端っこに足（？）をかけたとたん、あわれかたつむりは
突如睡魔におそわれ、ずりずり落ちて井戸の外には出れません。
そこで5日目にめでたく外に出られる。はじめの答えと同じ5日が答えなのです。
これは、問題の出し方の不十分さで、どちらが答えでもよくなります。
（ペンネ−ム：中数の基本）
１日に８−４＝４(ｍ)進むので，３日目の終り(＝４日目の初め)には，12(m)
のところにいます．そこで４日目の夕方には，指先(カタツムリに指がありまし
たっけ？)が出口に届きます．
ここからが，判断に迷うところです．ここで夜のうちにずり落ちてしまうと
考えるか，もう下がらないと考えるかは純数学なら約束で決まりますが，理科
の応用問題とすると，・・・カタツムリの足の裏は，カミソリの上でも渡れる
と言われており，吸着力が優れています．決して鍵のようなフックがあるわけ
ではありません．だからこそ，夜のうちに寝ているうちに「下がってしまう」
とされているので，４日目の夕方に指先が届いても体全体は出ていないし，指
先も「出て」いないわけです．
他方，水面から歩き始めたというのは，指先からシッポ(通俗的な言いまわし)
まで，水中で生活できるわけではないので，体長分だけ水面上に出ていたとも考
えられます．こう考えれば，４日目の夕方には体全体が地表に出ているので，
もう下がらないと言う見方もできます．
結局，おもしろい方を答に選ぶと５日・・・(答)
（ペンネ−ム：浜田 明巳）
いつものようにエクセルのマクロで解いてみました．
プログラム中に日本語を使って，なるべく見やすく作ってみました．
答は，４日間です．
Option Explicit
Sub Macro1()
Dim 日 As Integer
Dim 高さ As Integer
日 = 0
高さ = 0
While 高さ < 20
日 = 日 + 1
高さ = 高さ + 8
Cells(日, 1).Value = 日
Cells(日, 2).Value = 高さ
If 高さ < 20 Then
高さ = 高さ - 4
Cells(日, 3).Value = 高さ
End If
Wend
MsgBox "答は" + Str(日) + "日間です．", 48
End Sub
（ペンネ−ム：大阪府にお住まいのタクミケンスケさん ）
あきらくんが家につくまでには、２(ｋｍ/h)÷４(ｋｍ)で０．５（ｈ）。
愛犬ポチ(時速１０ｋｍ) は、０．５時間走るってことで、
１０×０．５＝５ よってポチは５ｋｍ走るのです．
（ペンネ−ム：たかし）
あきらくんは家まで３０分かかったことになる。その間、ポチも走りつづけたので
時速１０ｋｍ×０．５時間＝５ｋｍ
Answer:5km
（ペンネ−ム：ツァラトストラ）
結局ポチはあきらくんが家に着くまで走っている。
あきらくんは家に着くまで０．５時間かかるので時速１０
ｋｍのポチは５ｋｍ走る。答え５ｋｍ
（ペンネ−ム：ねこ）
あきらくんは家に着くまで２[ｋｍ]÷４[ｋｍ／ｈ]＝０．５ｈかかり、
その間ポチは時速１０ｋｍで走りつづけたのだから、
走った距離は１０[ｋｍ／ｈ]×０．５[ｈ]＝５ｋｍ。
（ペンネ−ム：やなせ）
ふたり（一人と１匹かな）のスピードを合算しないで、単純に
あきら君が家に帰るまでの時間を計算します。
その間ポチは走っているわけですから・・
２／４＝０．５時間
０．５時間×１０＝５で
答えは ５ｋｍ
（ペンネ−ム：水の流れ）
太郎さんは、この問題を子供が小学校のときに、質問を受けたことがありますので、
覚えています。勿論、数字までは記憶にないのですが。
さて、あきらくんと愛犬ポチは家に着くまで、同じ時間動いていることですから、
ポチの走った距離は、あきらくんが家に着く時間を求めて、時速を掛ければよいです。
２÷４＝０．５（時間）
したがって、ポチの走った距離は、１０（ｋｍ）×０．５（時間＝５（ｋｍ）
（ペンネ−ム：数楽家Ｃｒａｎｅ）
「向いあって走っている人の間を行き来しているハエ」とか、
「２人がキャッチボールをしながら近づいて行くときのボールの飛んだ距離」
など、色んなバージョンを見たことがあります。
答えはもちろん、あきらくんが家に着くのに30分かかる。
その間ポチは走りつづけているから５ｋｍ。
（ペンネ−ム：中数の基本）
あきらくんは２÷４＝0.5時間歩き，その間ずっとポチも歩きつづけるとする
と，ポチは 0.5×10＝５(km)走ります．
なお，家の手前数ｍのところでは，ポチの頭は家の方に向かったり，あきら
くんの方に向かったり，大変忙しくなります(無限回振り返ることとなり，特に
自分の頭の幅よりもあきらくんが近づいたときは，首を振っているだけという
状態になりますが，そこはおあいきょうということにしないと問題が解けません．)
５(km)・・・(答)
（ペンネ−ム：高橋 道広 ）
あきら君は2時間歩き、その間ぽちは走りっぱなし。ということは、２０ｋｍ走ったことになります。
これは、無限等比級数でも解けますね、きっと。
しかし、ここで気になることがあります。一つ目は、向きを変える時間が書いていないこと。
ですから、２０ｋｍ以下というのが答えでしょう。きっと。
もうひとつ気になるのは、あきら君がついたときに、ぽちはどっちのほうを向いていたかということ。
これは永遠のなぞです。夜も寝られなくなるかもしれません（古い…）
（ペンネ−ム：かつ）
ポチ君は家とあきら君との間を行ったり来たりする。
ここで問題なのは、ポチ君の距離なので、ポチ君が走る距離をいちいち場合わけして書いていく
こともできるが、ここでは「あきら君が何分歩いていたか？」と言うことがわかれば、
ポチ君の走った距離がわかります。
つまりポチ君もあきら君も同じ時間をかけることで同時に家に到着します。
よってあきら君の歩いている時間がわかればよいのです。
あきら君は２ｋｍの距離を時速４ｋｍで歩くので結局３０分（０．５時間）かかります。
よってポチ君も３０分間、時速１０ｋｍで走っているので・・・。
１０×０．５＝５
よって５ｋｍ
何回行き来したかは問題ではないのです。
（ペンネ−ム：夜ふかしのつらいおじさん ）
ポチは５ｋｍ走ったことになります。
（その１） （その２） （ペンネ−ム：Idaho Potato） あきらくんとポチが最初に再会するまでにポチが走る距離は 20/7 km。
その位置は家から 6/7 km。 …と、等比級数の計算をさせておいて、実は、 で、これだけでは単なるパズルに過ぎないので、
私からは次の問題を追加しましょう。 （ペンネ−ム：浜田 明巳） いつものようにエクセルのマクロで解いてみました．
プログラム中に日本語を使って，なるべく見やすく作ってみました． １．かたつむりの問題について、中数の基本さんの解答や
高橋 道広さんの解答を読んで、
私はげらげら笑ってしまいました。 ２．ポチの問題は、Idaho Potatoさんのご指摘の通りのおちをねらったのですが・・・!!? 最後に、Idaho Potatoさんから宿題が出ています。
みなさん、よろしくお願いします。 関連した内容が、
コロキウム室 NO.900にあります。
家からあきらくんとポチが出会ったところまでの距離をLn、家から次にあきら
くんとポチが出会うところまでの
距離をLn+1とします。
すると、あきらくんとポチが出会うまでの時間を考え
て、次の漸化式が成り立ちます。
（ Ln − Ln+1 ） ／ ４ ＝ （ Ln ＋ Ln+1 ） ／ １０
これを整理すると、
Ln+1 ＝ ３／７ Ln
これは、等比数列です。（初項は、２です）
ポチは、あきらくんと出あうまでに
L1 ＋ L2 ＋ L2 ＋ L3 ＋ L3 ＋ L4 ＋ L4 ＋ ・・・・
＝ ２ × （ L1 ＋ L2 ＋ L3 ＋ L4 ＋ ・・・・ ） − L1
＝ ２ ×２／（ １− ３／７） − ２
＝ ５
の距離を走ることになります。
解答・その１２
これは、4kmの道の両端からあきらくんとポチが 2:5 の速度で
向かい合って進むと考えるとわかりやすいでしょう。
次のステップは、同じことが最初の 3/7[=(6/7)/2] 倍のスケールで
繰り返されるので、ポチの走る距離は (20/7)×(3/7) km。
以下同様に、1ステップ進むごとに全体のスケールが 3/7 倍になるので、
ポチの走る距離は、初項 20/7 (km)、公比 3/7 の等比級数の和で、5km。
あきらくんが家に着くまでの時間は 1/2 時間、その間ポチは 10km/h で
走り続けるのだから、走った距離は 10×(1/2)=5 (km)。
と切り返すのがオチでしょうか(笑)。
「あきらくんが家に着いたとき、ポチの頭はどちらを向いているでしょう?」
(出発点の方向か、家の方向か?)
つまり、この問題には本質的にゼノンのパラドックスが潜んでいるのです。
解答・その１３
答は，５kmです．しかし答があっていても，近似解としてしか意味がありませんので，
この方法では数学的に解いたとはいえません．
Sub Macro2()
Cells(1, 1).Value = "経過時間(秒)"
Cells(1, 2).Value = "あきらくんの歩いた距離"
Cells(1, 3).Value = "ポチの位置"
Cells(1, 4).Value = "ポチの走った距離"
Columns("A:D").Select
Columns("A:D").EntireColumn.AutoFit
Range("D2").Select
Dim あきらくんの歩いた距離 As Double
Dim ポチの走った距離 As Double
Dim ポチの位置 As Double
Dim あきらくんの速度 As Double
Dim ポチの速度 As Double
Dim きざみ As Double
あきらくんの速度 = 4 / 60 / 60
ポチの速度 = 10 / 60 / 60
きざみ = 0.1
あきらくんの歩いた距離 = 0
ポチの走った距離 = 0
ポチの位置 = 0
Cells(2, 1).Value = 0
While あきらくんの歩いた距離 < 2
あきらくんの歩いた距離 = あきらくんの歩いた距離 + きざみ * あきらくんの速度
ポチの走った距離 = ポチの走った距離 + きざみ * Abs(ポチの速度)
ポチの位置 = ポチの位置 + きざみ * ポチの速度
If ポチの位置 >= 2 Then
Beep
ポチの走った距離 = ポチの走った距離 - (ポチの位置 - 2)
ポチの位置 = 2
ポチの速度 = -ポチの速度
ElseIf ポチの位置 <= あきらくんの歩いた距離 Then
Beep
ポチの走った距離 = ポチの走った距離 - (あきらくんの歩いた距離 - ポチの位置)
ポチの位置 = あきらくんの歩いた距離
ポチの速度 = -ポチの速度
End If
Cells(2, 1).Value = Cells(2, 1).Value + きざみ
Cells(2, 2).Value = あきらくんの歩いた距離
Cells(2, 3).Value = ポチの位置
Cells(2, 4).Value = ポチの走った距離
Wend
End Sub
正解者
水の流れ 中数の基本 KOSUGI
高橋 道広 kiyo 夜ふかしのつらいおじさん
浜田 明巳 ツァラトストラ teppei
Oitan 大阪府にお住まいのタクミケンスケさん ＳＨＯ
ねこ 数楽家Ｃｒａｎｅ かつ
佐々木一樹 kumapu 細井 夏樹
たかし kohda やなせ
Idaho Potato
まとめ
出題者としては、ただ数式を並べただけではおもしろくないから、いろいろな表現を工夫するわけですが、
そうすることで数学的な厳密さは失われるかもしれません。
そこは好意的にモデル化してほしい・・・・と思う反面、わざと意地悪な解釈をするのもまたおもしろいと思います。
数学はある意味では、理想的な状態を想定して解きますけれど、現実はそうはならなかったりしますからね。
一般に、初項がa、公比がｒの無限等比級数数列 a＋ar＋ar2＋ar3＋・・・は、
第ｎ項までの部分和が
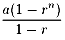
となることから、−１＜ｒ＜１の時に収束することがわかります。
そしてその和は
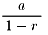
となります。
ですから−１＜ｒ＜１の無限等比級数は、この問題のように必ず別な解釈があるのではないかと思ってしまいます？！
E-mail
戻る
top