Weekend Mathematics／コロキウム室／テーマ別 ／11.大相撲本場所



コロキウム室(大相撲本場所)


NO.199 　　　 11/11 　　水の流れ 　　　 大相撲本場所（１）

今、旬なものは　大相撲九州場所ですね。
「偉大な横綱は連敗しないのが、優勝の条件のようです。 そこで、１５日間(2)連敗しない、勝ち負けの勝敗の起こり方は 何通りでしょう？また、一般の場合はどうなるでしょう？」



NO.201 　　　 11/14 　　 Junko 　　　 大相撲本場所（２）

１５試合中、２連敗(以上)しない場合の数を負け数で分類してみました。

重複組み合わせnＨrを使います。 詳しくは、こちら

  1. ０敗
    全勝するということで、１通り

  2. １敗
    ↓×↓
    この↓のところに、１４個の○を重複を許して（０でもよい）おくことになります。
    2Ｈ14=15Ｃ14=15Ｃ1=15

  3. ２敗
    ２つの×の間に、最低１個の○をおきます。
    ×○×
    ↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この３つの↓のところに、１２個の○を重複を許して（０でもよい）おくことになります。
    3Ｈ12=14Ｃ12=14Ｃ2=91

  4. ３敗
    ３つの×の間に、最低１個の○をおきます。
    ×○×○×
    ↓×○↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この４つの↓のところに、１０個の○を重複を許して（０でもよい）おくことになります。
    4Ｈ10=13Ｃ10=13Ｃ3=286

  5. ４敗
    ４つの×の間に、最低１個の○をおきます。
    ×○×○×○×
    ↓×○↓×○↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この５つの↓のところに、８個の○を重複を許して（０でもよい）おくことになります。
    5Ｈ8=12Ｃ8=12Ｃ4=495

  6. ５敗
    ５つの×の間に、最低１個の○をおきます。
    ×○×○×○×○×
    ↓×○↓×○↓×○↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この６つの↓のところに、６個の○を重複を許して（０でもよい）おくことになります。
    6Ｈ6=11Ｃ6=11Ｃ5=462

  7. ６敗
    ６つの×の間に、最低１個の○をおきます。
    ×○×○×○×○×○×
    ↓×○↓×○↓×○↓×○↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この７つの↓のところに、４個の○を重複を許して（０でもよい）おくことになります。
    7Ｈ4=10Ｃ4=10Ｃ6=210

  8. ７敗
    ７つの×の間に、最低１個の○をおきます。
    ×○×○×○×○×○×○×
    ↓×○↓×○↓×○↓×○↓×○↓×○↓×↓
    「○↓」は、「↓○」でもかまいません。
    この８つの↓のところに、２個の○を重複を許して（０でもよい）おくことになります。
    8Ｈ2=9Ｃ2=9Ｃ7=36

  9. ８敗
    ×○×○×○×○×○×○×○×の１通り
以上のことから、 
 1+2Ｈ14+3Ｈ12+4Ｈ10+5Ｈ8+6Ｈ6+7Ｈ4+8Ｈ2+1

=1+15Ｃ14+14Ｃ12+13Ｃ10+12Ｃ8+11Ｃ6+10Ｃ4+9Ｃ2+1

=1+15Ｃ1+14Ｃ2+13Ｃ3+12Ｃ4+11Ｃ5+10Ｃ6+9Ｃ7+1

=1+15+91+286+495+462+210+36+1

=1597


これを一般化するとどうなるか？
Ｎ試合中、２連敗(以上)しない場合の数を求めることになります。
上の例にならって、想像すると、
N+1Ｃ0+NＣ1+N-1Ｃ2+N-2Ｃ3+･･･
となるのでしょうか？
これをまとめることはできるのでしょうか？



NO.203 　　　 11/16 　　　 水の流れ 　　 大相撲本場所（３）

Junkoさんは○を間に入れておられましたが、 組み合わせのＣに持ち込むこともできます。
すなわち、×（負けの数）で場合分けします。 （でも、同じ考えですが）
×をｋ個（ｋ≧０）のとき、○（１５−ｋ）個です。
ただし、ｋ≧９のときは、明らかに不適。

  1. ｋ＝０のとき、○のみで１通り
  2. ｋ＞０のとき、×の起こりうる日は○両端及び間の
    　　　　１５−ｋ＋１＝１６−ｋ
    　　　よって、×の起こる日は16-kＣk（ｋ＝１，２，３，・・・，８）
したがって、その総数は 
　１＋15Ｃ1＋14Ｃ2＋13Ｃ3＋12Ｃ4＋・・・＋9Ｃ7＋8Ｃ8

＝１５９７
となります。



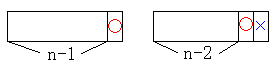
NO.207 　　　 11/19 　　　 水の流れ 　　 大相撲本場所（４）

大相撲の問題と２×ｎの長方形は同じ結果なのです。初項違いで。



NO.208 　　　 11/21 　　　 Junko 　　 大相撲本場所（５）

これもフィボナッチ数列なのですか？　ええ−っ、驚き！　
検証してみます。 Ｎ試合するとして、連敗(２連敗以上)しない、勝ち負けの勝敗の起こり方が ｆ(Ｎ)通りとします。
NO.201で確かめた結果から、 ｆ(１５)＝１５９７とかけるわけですよね。

Ｎ＝１から順に確かめてみます。

  • Ｎ＝１
    「○」か「×」の２通り。ｆ(１)＝２
  • Ｎ＝２
    「○○」「○×」「×○」の３通り。ｆ(２)＝３
  • Ｎ＝３
    「○○○」「○○×」「○×○」「×○○」「×○×」の５通り。ｆ(３)＝５
  • Ｎ＝４
    「○○○○」「○○○×」「○○×○」「○×○○」
    「×○○○」「×○×○」「×○○×」「○×○×」の８通り。ｆ(４)＝８
確かにフィボナッチ数列のような雰囲気・・・。
フィボナッチ数列を定義づけている漸化式、 ｆ(Ｎ−２)＋ｆ(Ｎ−１)＝ｆ(Ｎ)に代入してみると、
ｆ(５)＝１３、ｆ(６)＝２１、ｆ(７)＝３４、 ｆ(８)＝５５、ｆ(９)＝８９、ｆ(１０)＝１４４、 ｆ(１１)＝２３３、ｆ(１２)＝３７７、ｆ(１３)＝６１０、 ｆ(１４)＝９８７、ｆ(１５)＝１５９７ というわけで、確かに先程の結果と一致します。
う−ん、としばらく考えて・・・
なるほど連敗(２連敗以上)しないということは、 次の２つのケ−スがあるということに思い至りました。
１つは、(Ｎ−１)試合目までがどうであれ、Ｎ試合目に勝てばいいわけです。
もう１つはＮ試合目に負ける場合ですが、 これは(Ｎ−１)試合目が勝った場合にのみ許されるわけです。 この時、(Ｎ−２)試合目までの勝敗は問いません。

つまりこの場合もまた確かに、
ｆ(Ｎ−２)＋ｆ(Ｎ−１)＝ｆ(Ｎ)が成立しているのです。

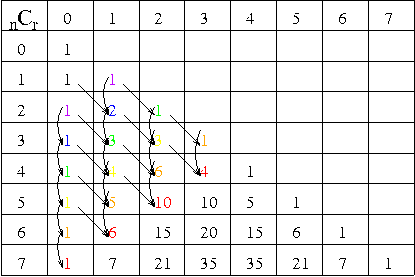
この問題をNO.201では、組み合わせ(Combination)を使って解きました。 ということは、フィボナッチ数(フィボナッチ数列に登場する数をこう呼びます。)は、 必ず組み合わせ(Combination)の和として表せるということなのでしょうか？



NO.211 　　　 11/22 　　　水の流れ 　　　 大相撲本場所（６）

参考図のようなパスカルの三角形（二項係数）を斜めに足すと、 フィボナッチ数列になります。

＜参考図＞　パスカルの三角形（二項係数）

ｎＣｒ ０１２３ ４５６７
０ １        
１ １１       
２ １２１      
３ １３３１     
４ １４６４ １   
５ １５１０１０ ５１  
６ １６１５２０ １５６１ 
７ １７２１３５ ３５２１７１

数式でかくと、次のようになります。

フィボナッチ数列をＦ(ｎ)とすると、Ｆ(１)＝１、Ｆ(２)＝１、Ｆ(３)＝１＋１＝２、 Ｆ(４)＝１＋２＝３、Ｆ(５)＝２＋３＝５、・・・

Ｆ(ｎ＋１)＝ｎＣ０＋ｎ−１Ｃ１＋ ｎ−２Ｃ２＋・・・＋ｍＣｍ

Ｆ(ｎ＋２)＝ｎ＋１Ｃ０＋ｎＣ１＋ ｎ−１Ｃ２＋・・・＋ｍ＋１Ｃｍ
ただし、ｎ＝２ｍで、ｍ≧１、ｎ≧２の自然数とする。２つの組みで考える。




NO.213 　　　 11/25 　　　Junko 　　　 大相撲本場所（７）

NO.211にあるパスカルの三角形を見て、 本当にびっくり、感激しました。 確かに斜めに足していくとフィボナッチ数が現れてきます。 こんなところでつながっているとは！　神秘を感じます。



NO.214 　　　 11/25 　　　水の流れ 　　　 大相撲本場所（８）

大相撲の問題の続きです。
もし、３連敗しない方法（２連敗まで許される）場合は 　１，２，３，４，・・・、１５日ではどんな数列に なるでしょう。長方形の問題ではどんな変化になるでしょう？



　　　　　　　　　　　　　　　　　　　　　　　　　　　

NO.215 　　　 11/28 　　　ヴァー 　　　 大相撲本場所（９）

水の流れさんのNo.211の主張が，その主張どおりフィボナッチ数列の式「F(n)+F(n+1)=F(n+2)」を満たしていることを証明してみましょう．
この証明では，組合せ「nCr」について常に成り立つ等式(恒等式)

nCr+nCr+1=n+1Cr+1

を利用します．

＜ F(2m)+F(2m+1)=F(2m+2) の証明 ＞

まず，No.211から，

F(2m) = 2m-1C0 + 2m-2C1 + .. + mCm-1
F(2m+1) = 2mC0 + 2m-1C1 + 2m-2C2 + .. + mCm

であり，この2つの式を足し合わせると，

左辺 = F(2m)+F(2m+1)

で，

右辺 = 2mC0
+(2m-1C0+2m-1C1)
+(2m-2C1+2m-2C2)
+...
+(mCm-1+mCm)
= 2m+1C0+2mC1+2m+1C2+...+m+1Cm
= F(2m+2)

になります．
ここでは，はじめの項では，2mC0=2m+1C0を用いていて，( )の部分では先の等式を用いています．

＜F(2m+1)+F(2m+2)=F(2m+3) の証明 ＞

先程と同じく，No.211から，

F(2m+1) = 2mC0 + 2m-1C1 + .. + m+1Cm-1 + mCm
F(2m+2) = 2m+1C0 + 2mC1 + 2m-1C2 + .. + m+1Cm

であり，この2つの式を足し合わせると，

左辺 = F(2m+1)+F(2m+2)

で，

右辺 = 2m+1C0
+(2mC0+2mC1)
+(2m-1C1+2m-1C2)
+...
+(m+1Cm-1+m+1Cm)
+mCm
= 2m+2C0+2m+1C1+2mC2+...+m+2Cm+m+1Cm+1
= F(2m+3)

になります．
ここでは，はじめの項では，2m+1C0=2m+2C0を用いていて，同じように最後の項では，mCm=m+1Cm+1を用いています．
また，( )の部分では先の等式を用いています．

この証明は，No.211の表に対応させると次のようなことを表しています．

例えば，赤の部分は，黄色とオレンジの数字の和になっていることを表しています．
同じマスに2つの矢印が流れ込んでいるのがその「和」になっていることを示しています．



NO.216 　　　 12/1 　　Junko 　　　 大相撲本場所（１０）

Ｎ試合中、３連敗しない（２連敗までは許される）場合の数 をＧ(Ｎ)とします。

具体的にいくつか調べてみます。

  1. Ｎ＝１
    「○」か「×」　より、Ｇ(１)＝２
  2. Ｎ＝２
    「○○」「○×」「×○」「××」より、Ｇ(２)＝４
  3. Ｎ＝３
    「○○○」「○○×」「○×○」「×○○」
    「○××」「×○×」「××○」より、Ｇ(３)＝７
  4. Ｎ＝４
    「○○○○」「○○○×」「○○×○」「○×○○」「×○○○」
    「○○××」「○××○」「××○○」「○×○×」「×○×○」
    「×○○×」「××○×」「×○××」　より、Ｇ(４)＝１３
ここまで調べて考える・・・。
Ｇ(ｎ)＋Ｇ(ｎ＋１)＋Ｇ(ｎ＋２)＝Ｇ(ｎ＋３) 　ただし、ｎ≧１という性質を持っているかのかな？
フィボナッチ数列とよく似ていますね。
この漸化式について次のように考えます。


次の３つのケ−スに場合分けできます。
１つは、(Ｎ−１)試合目までがどうであれ、Ｎ試合目に勝てばいいわけです。
２つめはＮ試合目に負ける場合ですが、 これは(Ｎ−１)試合目が勝った場合にはＯＫです。 この時、(Ｎ−２)試合目までの勝敗は問いません。
更に３つ目は、Ｎ試合目に負けて、(Ｎ−１)試合目も負けた場合ですが、 これは(Ｎ−２)試合目に勝っていればＯＫです。
というわけで、Ｇ(ｎ)＋Ｇ(ｎ＋１)＋Ｇ(ｎ＋２)＝Ｇ(ｎ＋３) という漸化式が成り立っているというわけです。



NO.217 　　　 12/1 　　水の流れ 　　　 大相撲本場所（１１）

この数列をトリボナッチ数列といいます。 トリボナッチは人の名前ではありません。 １つの数が前の３つ（トリ）の数の和で得られるので、 フィボナッチ数列の拡張です。



戻る